Равномерные мозаики в гиперболической плоскости - Uniform tilings in hyperbolic plane

Примеры равномерных мозаик
СферическийЕвклидовоГиперболический
Равномерная черепица 532-t0.png
{5,3}
5.5.5
CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node.png		Равномерная черепица 63-t0.png
{6,3}
6.6.6
CDel node 1.pngCDel 6.pngCDel node.pngCDel 3.pngCDel node.png		Шестиугольная черепица.svg
{7,3}
7.7.7
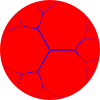CDel node 1.pngCDel 7.pngCDel node.pngCDel 3.pngCDel node.png		H2-I-3-dual.svg
{∞,3}
∞.∞.∞
CDel node 1.pngCDel infin.pngCDel node.pngCDel 3.pngCDel node.png
Регулярные мозаики сферы {p, q}, евклидовой плоскости и гиперболической плоскости с использованием правильных пятиугольных, шестиугольных, семиугольных и апейрогональных граней.
Равномерная черепица 532-t01.png
т {5,3}
10.10.3
CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png		Равномерная черепица 63-t01.png
т {6,3}
12.12.3
CDel node 1.pngCDel 6.pngCDel node 1.pngCDel 3.pngCDel node.png		Усеченный семиугольный tiling.svg
т {7,3}
14.14.3
CDel node 1.pngCDel 7.pngCDel node 1.pngCDel 3.pngCDel node.png		Плитка H2 23i-3.png
т {∞, 3}
∞.∞.3
CDel node 1.pngCDel infin.pngCDel node 1.pngCDel 3.pngCDel node.png
Усеченные мозаики имеют фигуры вершин 2p.2p.q из регулярных {p, q}.
Равномерная черепица 532-t1.png
г {5,3}
3.5.3.5
CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png		Равномерная черепица 63-t1.png
г {6,3}
3.6.3.6
CDel node.pngCDel 6.pngCDel node 1.pngCDel 3.pngCDel node.png		Тригептагональный тайлинг.svg
г {7,3}
3.7.3.7
CDel node.pngCDel 7.pngCDel node 1.pngCDel 3.pngCDel node.png		H2 мозаика 23i-2.png
г {∞, 3}
3.∞.3.∞
CDel node.pngCDel infin.pngCDel node 1.pngCDel 3.pngCDel node.png
Квазирегулярные мозаики похожи на правильные мозаики, но чередуют два типа правильных многоугольников вокруг каждой вершины.
Равномерная черепица 532-t02.png
рр {5,3}
3.4.5.4
CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.png		Равномерная черепица 63-t02.png
рр {6,3}
3.4.6.4
CDel node 1.pngCDel 6.pngCDel node.pngCDel 3.pngCDel node 1.png		Ромбитригептагональная плитка.svg
рр {7,3}
3.4.7.4
CDel node 1.pngCDel 7.pngCDel node.pngCDel 3.pngCDel node 1.png		H2 мозаика 23i-5.png
rr {∞, 3}
3.4.∞.4
CDel node 1.pngCDel infin.pngCDel node.pngCDel 3.pngCDel node 1.png
Полуправильные мозаики иметь более одного типа правильных многоугольников.
Равномерная черепица 532-t012.png
tr {5,3}
4.6.10
CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png		Равномерная черепица 63-t012.svg
tr {6,3}
4.6.12
CDel node 1.pngCDel 6.pngCDel node 1.pngCDel 3.pngCDel node 1.png		Усеченный трехгептагональный тайлинг.svg
tr {7,3}
4.6.14
CDel node 1.pngCDel 7.pngCDel node 1.pngCDel 3.pngCDel node 1.png		H2 мозаика 23i-7.png
tr {∞, 3}
4.6.∞
CDel node 1.pngCDel infin.pngCDel node 1.pngCDel 3.pngCDel node 1.png
Омниусеченные мозаики иметь три или более четных правильных многоугольника.

В гиперболический геометрия, а однородная гиперболическая мозаика (или регулярное, квазирегулярное или полуправильное гиперболическое разбиение) - это заполнение от края до края гиперболической плоскости, которое имеет правильные многоугольники в качестве лица и является вершинно-транзитивный (переходный на его вершины, изогонально, т.е. имеется изометрия отображение любой вершины на любую другую). Отсюда следует, что все вершины конгруэнтный, а черепица имеет высокую степень вращательного и поступательного симметрия.

Равномерные мозаики можно идентифицировать по их конфигурация вершины, последовательность чисел, представляющая количество сторон многоугольника вокруг каждой вершины. Например, 7.7.7 представляет собой семиугольная черепица который имеет 3 семиугольники вокруг каждой вершины. Он также является правильным, поскольку все многоугольники имеют одинаковый размер, поэтому ему также можно присвоить Символ Шлефли {7,3}.

Однородные мозаики могут быть обычный (если также транзитивны по граням и ребрам), квазирегулярны (если транзитивны по ребрам, но не транзитивны по граням) или полурегулярный (если ни ребро, ни грань не транзитивны). Для прямоугольных треугольников (п q 2) есть две правильные мозаики, представленные Символ Шлефли {п,q} и {q,п}.

Строительство Wythoff

Пример конструкции Wythoff с прямоугольными треугольниками (р = 2) и 7 образующих точек. Линии к активным зеркалам окрашены в красный, желтый и синий цвет, а 3 узла напротив них связаны символом Wythoff.

Существует бесконечное количество однородных мозаик, основанных на Треугольники Шварца (п q р) куда 1/п + 1/q + 1/р <1, где п, q, р - порядки симметрии отражения в трех точках фундаментальный доменный треугольник - группа симметрии гиперболическая группа треугольников.

Каждое семейство симметрий содержит 7 однородных мозаик, определяемых Символ Wythoff или же Диаграмма Кокстера-Дынкина, 7 представляют собой комбинации из 3 активных зеркал. 8-й представляет собой чередование операция, удаляющая альтернативные вершины из высшей формы со всеми активными зеркалами.

Семьи с р = 2 содержат регулярные гиперболические мозаики, определяемый Группа Коксетера такие как [7,3], [8,3], [9,3], ... [5,4], [6,4], ....

Гиперболические семьи с р = 3 или больше даются как (п q р) и включают (4 3 3), (5 3 3), (6 3 3) ... (4 4 3), (5 4 3), ... (4 4 4) ....

Гиперболические треугольники (п q р) определяют компактные равномерные гиперболические мозаики. В пределе любой из п, q или же р может быть заменен на ∞, который определяет паракомпактный гиперболический треугольник и создает однородные мозаики с любой из бесконечных граней (называемых апейрогоны ), которые сходятся к одной идеальной точке или бесконечной вершинной фигуре с бесконечным числом ребер, расходящихся из одной и той же идеальной точки.

Больше семейств симметрии можно построить из фундаментальных областей, не являющихся треугольниками.

Выбранные семейства однородных мозаик показаны ниже (с использованием Модель диска Пуанкаре для гиперболической плоскости). Трое из них - (7 3 2), (5 4 2) и (4 3 3) - и никакие другие не являются минимальный в том смысле, что если любое из их определяющих чисел заменить меньшим целым числом, результирующий образец будет либо евклидовым, либо сферическим, а не гиперболическим; и наоборот, любое из чисел может быть увеличено (даже до бесконечности) для создания других гиперболических паттернов.

Каждая однородная мозаика порождает двойная равномерная мозаика, многие из которых также приведены ниже.

Области прямоугольного треугольника

Их бесконечно много (п q 2) группа треугольников семьи. В этой статье показана обычная мозаика до п, q = 8, и равномерные мозаики в 12 семейств: (7 3 2), (8 3 2), (5 4 2), (6 4 2), (7 4 2), (8 4 2), (5 5 2) ), (6 5 2) (6 6 2), (7 7 2), (8 6 2) и (8 8 2).

Регулярные гиперболические мозаики

Простейшим набором гиперболических мозаик являются регулярные мозаики {п,q}, которые существуют в матрице с правильными многогранниками и евклидовыми мозаиками. Правильная мозаика {п,q} имеет двойную мозаику {q,п} по диагональной оси таблицы. Самодвойственные мозаики {2,2}, {3,3}, {4,4}, {5,5} и т.д. проходят по диагонали стола.

(7 3 2)

В (7 3 2) группа треугольников, Группа Коксетера [7,3], орбифолд (* 732) содержит эти однородные мозаики:

(8 3 2)

В (8 3 2) группа треугольников, Группа Коксетера [8,3], орбифолд (* 832) содержит эти однородные мозаики:

(5 4 2)

В (5 4 2) группа треугольников, Группа Коксетера [5,4], орбифолд (* 542) содержит эти однородные мозаики:

(6 4 2)

В (6 4 2) группа треугольников, Группа Коксетера [6,4], орбифолд (* 642) содержит эти однородные мозаики. Поскольку все элементы четные, каждый однородный двойной мозаичный элемент представляет фундаментальную область отражательной симметрии: * 3333, * 662, * 3232, * 443, * 222222, * 3222 и * 642 соответственно. Кроме того, можно чередовать все 7 однородных плиток, а также у них есть двойники.

(7 4 2)

В (7 4 2) группа треугольников, Группа Коксетера [7,4], орбифолд (* 742) содержит эти однородные мозаики:

(8 4 2)

В (8 4 2) группа треугольников, Группа Коксетера [8,4], орбифолд (* 842) содержит эти однородные мозаики. Поскольку все элементы четные, каждый однородный двойной мозаичный элемент представляет фундаментальную область отражательной симметрии: * 4444, * 882, * 4242, * 444, * 22222222, * 4222 и * 842 соответственно. Кроме того, можно чередовать все 7 однородных плиток, а также у них есть двойники.

(5 5 2)

В (5 5 2) группа треугольников, Группа Коксетера [5,5], орбифолд (* 552) содержит эти однородные мозаики:

(6 5 2)

В (6 5 2) группа треугольников, Группа Коксетера [6,5], орбифолд (* 652) содержит эти однородные мозаики:

(6 6 2)

В (6 6 2) группа треугольников, Группа Коксетера [6,6], орбифолд (* 662) содержит эти однородные мозаики:

(8 6 2)

В (8 6 2) группа треугольников, Группа Коксетера [8,6], орбифолд (* 862) содержит эти однородные мозаики.

(7 7 2)

В (7 7 2) группа треугольников, Группа Коксетера [7,7], орбифолд (* 772) содержит эти однородные мозаики:

(8 8 2)

В (8 8 2) группа треугольников, Группа Коксетера [8,8], орбифолд (* 882) содержит эти однородные мозаики:

Общие области треугольников

Есть бесконечно много общих группа треугольников семьи (п q р). В этой статье показаны однородные мозаики в 9 семействах: (4 3 3), (4 4 3), (4 4 4), (5 3 3), (5 4 3), (5 4 4), (6 3 3) , (6 4 3) и (6 4 4).

(4 3 3)

В (4 3 3) группа треугольников, Группа Коксетера [(4,3,3)], орбифолд (* 433) содержит эти однородные мозаики. Без прямых углов в основном треугольнике Конструкции Wythoff немного отличаются. Например, в (4,3,3) семья треугольников, то пренебрежительно Форма имеет шесть многоугольников вокруг вершины, а двойственная форма состоит из шестиугольников, а не пятиугольников. В целом вершина фигуры курносой мозаики в треугольнике (п,q,р) является p. 3.q.3.r.3, в данном случае ниже 4.3.3.3.3.3.

(4 4 3)

В (4 4 3) группа треугольников, Группа Коксетера [(4,4,3)], орбифолд (* 443) содержит эти однородные мозаики.

(4 4 4)

В (4 4 4) группа треугольников, Группа Коксетера [(4,4,4)], орбифолд (* 444) содержит эти однородные мозаики.

(5 3 3)

В (5 3 3) группа треугольников, Группа Коксетера [(5,3,3)], орбифолд (* 533) содержит эти однородные мозаики.

(5 4 3)

В (5 4 3) группа треугольников, Группа Коксетера [(5,4,3)], орбифолд (* 543) содержит эти однородные мозаики.

(5 4 4)

В (5 4 4) группа треугольников, Группа Коксетера [(5,4,4)], орбифолд (* 544) содержит эти однородные мозаики.

(6 3 3)

В (6 3 3) группа треугольников, Группа Коксетера [(6,3,3)], орбифолд (* 633) содержит эти однородные мозаики.

(6 4 3)

В (6 4 3) группа треугольников, Группа Коксетера [(6,4,3)], орбифолд (* 643) содержит эти однородные мозаики.

(6 4 4)

В (6 4 4) группа треугольников, Группа Коксетера [(6,4,4)], орбифолд (* 644) содержит эти однородные мозаики.

Сводка мозаик с конечными треугольными фундаментальными областями

Для таблицы всех равномерных гиперболических мозаик с фундаментальными областями (п q р), где 2 ≤ п,q,р ≤ 8.

Видеть Шаблон: Таблица конечных треугольных гиперболических мозаик

Четырехугольные области

Четырехугольная область имеет 9 позиций образующих точек, которые определяют однородные мозаики. Фигуры вершин указаны для общей симметрии орбифолда *pqrs, с 2-угольными гранями, вырождающимися в ребра.

(3 2 2 2)

Пример равномерных мозаик симметрии * 3222

Четырехугольные фундаментальные области также существуют в гиперболической плоскости, причем *3222 орбифолд ([∞, 3, ∞] обозначение Кокстера) как наименьшее семейство. Есть 9 мест генерации для равномерного замощения в четырехугольных областях. Фигура вершины может быть извлечена из фундаментальной области как 3 случая (1) угол, (2) средний край и (3) центр. При создании точек углы, смежные с углами порядка 2, вырождены {2} Digon лица в этих углах существуют, но их можно игнорировать. Курносый и чередовались равномерные мозаики также могут быть сгенерированы (не показаны), если фигура вершины содержит только четные грани.

Диаграммы Кокстера четырехугольных областей рассматриваются как вырожденный тетраэдр граф с 2 из 6 ребер, помеченных как бесконечность или пунктирные линии. Логическое требование, чтобы по крайней мере одно из двух параллельных зеркал было активным, ограничивает единые случаи до 9, а другие кольцевые шаблоны недопустимы.

(3 2 3 2)

Области идеального треугольника

Бесконечно много группа треугольников семьи, включая бесконечные заказы. В этой статье показаны равномерные мозаики в 9 семействах: (∞ 3 2), (∞ 4 2), (∞ ∞ 2), (∞ 3 3), (∞ 4 3), (∞ 4 4), (∞ ∞ 3) , (∞ ∞ 4) и (∞ ∞ ∞).

(∞ 3 2)

Идеал (∞ 3 2) группа треугольников, Группа Коксетера [∞,3], орбифолд (* ∞32) содержит эти равномерные мозаики:

(∞ 4 2)

Идеал (∞ 42) группа треугольников, Группа Коксетера [∞,4], орбифолд (* ∞42) содержит эти равномерные мозаики:

(∞ 5 2)

Идеал (∞ 5 2) группа треугольников, Группа Коксетера [∞,5], орбифолд (* ∞52) содержит эти равномерные мозаики:

(∞ ∞ 2)

Идеал (∞ ∞ 2) группа треугольников, Группа Коксетера [∞,∞], орбифолд (* ∞∞2) содержит эти равномерные мозаики:

(∞ 3 3)

Идеал (∞ 3 3) группа треугольников, Группа Коксетера [(∞,3,3)], орбифолд (* ∞33) содержит эти равномерные мозаики.

(∞ 4 3)

Идеал (∞ 4 3) группа треугольников, Группа Коксетера [(∞,4,3)], орбифолд (* ∞43) содержит эти равномерные мозаики:

(∞ 4 4)

Идеал (∞ 4 4) группа треугольников, Группа Коксетера [(∞,4,4)], орбифолд (* ∞44) содержит эти равномерные мозаики.

(∞ ∞ 3)

Идеал (∞ ∞ 3) группа треугольников, Группа Коксетера [(∞,∞,3)], орбифолд (* ∞∞3) содержит эти равномерные мозаики.

(∞ ∞ 4)

Идеал (∞ ∞ 4) группа треугольников, Группа Коксетера [(∞,∞,4)], орбифолд (* ∞∞4) содержит эти равномерные мозаики.

(∞ ∞ ∞)

Идеал (∞ ∞ ∞) группа треугольников, Группа Коксетера [(∞,∞,∞)], орбифолд (* ∞∞∞) содержит эти равномерные мозаики.

Сводка мозаик с бесконечными треугольными фундаментальными областями

Для таблицы всех равномерных гиперболических мозаик с фундаментальными областями (п q р), где 2 ≤ п,q,р ≤ 8 и один или несколько при ∞.

Рекомендации

  • Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN  978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)

внешняя ссылка