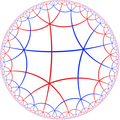
Тетрагексагональная черепица - Tetrahexagonal tiling
| Тетрагексагональная черепица | |
|---|---|
 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболическая равномерная мозаика |
| Конфигурация вершины | (4.6)2 |
| Символ Шлефли | г {6,4} или рр {6,6} г (4,4,3) т0,1,2,3(∞,3,∞,3) |
| Символ Wythoff | 2 | 6 4 |
| Диаграмма Кокстера | |
| Группа симметрии | [6,4], (*642) [6,6], (*662) [(4,4,3)], (*443) [(∞,3,∞,3)], (*3232) |
| Двойной | Квазирегулярная ромбическая мозаика порядка 6-4 |
| Характеристики | Вершинно-транзитивный реберно-транзитивный |
В геометрия, то тетрагексагональная черепица является равномерным замощением гиперболическая плоскость. Она имеет Символ Шлефли г {6,4}.
Конструкции
Есть для однородных построений этого тайлинга, три из них построены удалением зеркала из [6,4] калейдоскоп. Удаление последнего зеркала, [6,4,1+], дает [6,6], (* 662). Удаление первого зеркала [1+, 6,4], дает [(4,4,3)], (* 443). Удаление обоих зеркал как [1+,6,4,1+], оставляя [(3, ∞, 3, ∞)] (* 3232).
| Униформа Окраска |  |  |  |  |
|---|---|---|---|---|
| Фундаментальный Домены |  |  |  |  |
| Schläfli | г {6,4} | г {4,6}1⁄2 | г {6,4}1⁄2 | г {6,4}1⁄4 |
| Симметрия | [6,4] (*642) | [6,6] = [6,4,1+] (*662) | [(4,4,3)] = [1+,6,4] (*443) | [(∞,3,∞,3)] = [1+,6,4,1+] (*3232) |
| Символ | г {6,4} | рр {6,6} | г (4,3,4) | т0,1,2,3(∞,3,∞,3) |
| Coxeter диаграмма |
Симметрия
Двойная мозаика, называемая ромбическая тетрагексагональная мозаика, с конфигурация лица V4.6.4.6, и представляет основные области четырехугольного калейдоскопа, орбифолд (* 3232), показанный здесь в двух разных центрах обзора. Добавление точки 2-кратного вращения в центре каждого ромба представляет собой орбифолд (2 * 32).
Связанные многогранники и мозаика
| *п42 изменения симметрии квазирегулярных мозаик: (4.п)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *4п2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | |||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | [пя, 4] | |
| Цифры |  |  |  |  |  |  |  | |
| Конфиг. | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.пя)2 |
| Изменение симметрии квазирегулярных мозаик: 6.n.6.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия * 6n2 [n, 6] | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | |||||||
| *632 [3,6] | *642 [4,6] | *652 [5,6] | *662 [6,6] | *762 [7,6] | *862 [8,6]... | *∞62 [∞,6] | [iπ / λ, 6] | ||||
| Квазирегулярный цифры конфигурация |  6.3.6.3 |  6.4.6.4 |  6.5.6.5 |  6.6.6.6 |  6.7.6.7 |  6.8.6.8 |  6.∞.6.∞ | 6.∞.6.∞ | |||
| Двойные цифры | |||||||||||
| Ромбический цифры конфигурация |  V6.3.6.3 |  V6.4.6.4 |  V6.5.6.5 |  V6.6.6.6 | V6.7.6.7 |  V6.8.6.8 |  V6.∞.6.∞ | ||||
| Равномерные тетрагексагональные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,4], (*642 ) (с подсимметрией [6,6] (* 662), [(4,3,3)] (* 443), [∞, 3, ∞] (* 3222) индекса 2) (И [(∞, 3, ∞, 3)] (* 3232) подсимметрия индекса 4) | |||||||||||
= = = | = | = = = | = | = = = | = | ||||||
 |  |  |  |  |  |  | |||||
| {6,4} | т {6,4} | г {6,4} | т {4,6} | {4,6} | rr {6,4} | tr {6,4} | |||||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  | |||||
| V64 | V4.12.12 | V (4,6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Чередования | |||||||||||
| [1+,6,4] (*443) | [6+,4] (6*2) | [6,1+,4] (*3222) | [6,4+] (4*3) | [6,4,1+] (*662) | [(6,4,2+)] (2*32) | [6,4]+ (642) | |||||
= | = | = | = | = | = | ||||||
 |  |  |  |  |  |  | |||||
| ч {6,4} | с {6,4} | ч. {6,4} | с {4,6} | ч {4,6} | чрр {6,4} | sr {6,4} | |||||
| Однородные шестиугольные мозаики | ||||||
|---|---|---|---|---|---|---|
| Симметрия: [6,6], (*662) | ||||||
= | = | = | = | = | = | = |
 |  |  |  |  |  |  |
| {6,6} = ч {4,6} | т {6,6} = h2{4,6} | г {6,6} {6,4} | т {6,6} = h2{4,6} | {6,6} = ч {4,6} | рр {6,6} г {6,4} | тр {6,6} т {6,4} |
| Униформа двойников | ||||||
 |  |  |  |  |  |  |
| V66 | V6.12.12 | V6.6.6.6 | V6.12.12 | V66 | V4.6.4.6 | V4.12.12 |
| Чередования | ||||||
| [1+,6,6] (*663) | [6+,6] (6*3) | [6,1+,6] (*3232) | [6,6+] (6*3) | [6,6,1+] (*663) | [(6,6,2+)] (2*33) | [6,6]+ (662) |
 |  |  |  |  | ||
| ч {6,6} | с {6,6} | ч. {6,6} | с {6,6} | ч {6,6} | чрр {6,6} | sr {6,6} |
| Равномерные (4,4,3) мозаики | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [(4,4,3)] (*443) | [(4,4,3)]+ (443) | [(4,4,3+)] (3*22) | [(4,1+,4,3)] (*3232) | |||||||
 |  |  |  |  |  |  |  |  |  |  |
| ч {6,4} т0(4,4,3) | час2{6,4} т0,1(4,4,3) | {4,6}1/2 т1(4,4,3) | час2{6,4} т1,2(4,4,3) | ч {6,4} т2(4,4,3) | г {6,4}1/2 т0,2(4,4,3) | т {4,6}1/2 т0,1,2(4,4,3) | с {4,6}1/2 с (4,4,3) | ч. {4,6}1/2 час (4,3,4) | ч {4,6}1/2 ч (4,3,4) | q {4,6} час1(4,3,4) |
| Униформа двойников | ||||||||||
 |  |  |  | |||||||
| V (3,4)4 | V3.8.4.8 | V (4,4)3 | V3.8.4.8 | V (3,4)4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V (4.4.3)2 | V66 | V4.3.4.6.6 |
| Подобные мозаики H2 в симметрии * 3232 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Coxeter диаграммы | ||||||||
| Вершина фигура | 66 | (3.4.3.4)2 | 3.4.6.6.4 | 6.4.6.4 | ||||
| Изображение |  |  |  |  | ||||
| Двойной |  |  | ||||||
Смотрите также
- Квадратная плитка
- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.