Усеченная пятигексагональная черепица - Truncated pentahexagonal tiling
| Усеченная пятигексагональная черепица | |
|---|---|
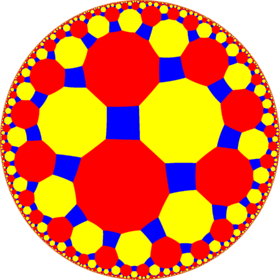 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболическая равномерная мозаика |
| Конфигурация вершины | 4.10.12 |
| Символ Шлефли | tr {6,5} или |
| Символ Wythoff | 2 6 5 | |
| Диаграмма Кокстера | |
| Группа симметрии | [6,5], (*652) |
| Двойной | Заказать 5-6 кисромбилей |
| Характеристики | Вершинно-транзитивный |
В геометрия, то усеченная тетрагексагональная мозаика является полуправильным замощением гиперболической плоскости. Есть один квадрат, один десятиугольник, и один двенадцатигранник на каждой вершина. Она имеет Символ Шлефли из т0,1,2{6,5}. Его название несколько вводит в заблуждение: буквальное геометрическое усечение пятигексагональная черепица создает прямоугольники вместо квадратов.
Двойная черепица
 |  |
| Двойственный тайлинг называется Заказ-5-6 мозаика кисромбиля, выполненный как полное деление пополам гексагональная черепица порядка 5, здесь треугольники показаны чередующимися цветами. Этот тайлинг представляет собой фундаментальные треугольные области симметрии [6,5] (* 652). | |
Симметрия
Есть четыре малых индексных подгруппы из [6,5] путем удаления и чередования зеркал. На этих изображениях основные области попеременно окрашены в черный и белый цвета, а на границах между цветами существуют зеркала.
| Индекс | 1 | 2 | 6 | |
|---|---|---|---|---|
| Диаграмма | 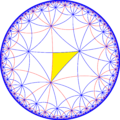 | 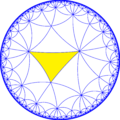 |  |  |
| Coxeter (орбифолд ) | [6,5] = (*652) | [1+,6,5] = (*553 ) | [6,5+] = (5*3) | [6,5*] = (*33333 ) |
| Прямые подгруппы | ||||
| Индекс | 2 | 4 | 12 | |
| Диаграмма |  |  |  | |
| Coxeter (орбифолд) | [6,5]+ = (652) | [6,5+]+ = (553) | [6,5*]+ = (33333) | |
Связанные многогранники и мозаики
Из Строительство Wythoff четырнадцать гиперболических однородные мозаики это может быть основано на регулярной шестиугольной мозаике порядка 5.
Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, мы получаем 7 форм с полной [6,5] симметрией и 3 с подсимметрией.
| Однородные шестиугольные / пятиугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,5], (*652) | [6,5]+, (652) | [6,5+], (5*3) | [1+,6,5], (*553) | ||||||||
 |  |  |  |  |  |  |  |  | |||
| {6,5} | т {6,5} | г {6,5} | 2t {6,5} = t {5,6} | 2r {6,5} = {5,6} | рр {6,5} | тр {6,5} | sr {6,5} | с {5,6} | ч {6,5} | ||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  | |||||
| V65 | V5.12.12 | V5.6.5.6 | V6.10.10 | V56 | V4.5.4.6 | V4.10.12 | V3.3.5.3.6 | V3.3.3.5.3.5 | В (3,5)5 | ||
Смотрите также
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.



