Антипризма - Antiprism

Униформа п-гональные антипризмы
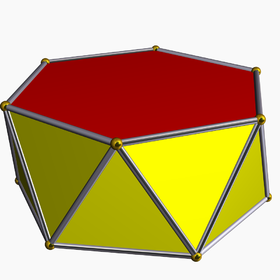Пример шестиугольной антипризмы
Тип	униформа в смысле полуправильный многогранник
Лица	2 п-угольники, 2п треугольники
Края	4п
Вершины	2п
Обозначения многогранника Конвея	Ап
Конфигурация вершины	3.3.3.п
Символ Шлефли	{ }⊗{п}^[1] с {2,2п} sr {2,п}
Диаграммы Кокстера
Группа симметрии	D_пd, [2⁺,2п], (2*п), порядок 4п
Группа вращения	D_п, [2,п]⁺, (22п), порядок 2п
Двойной многогранник	выпуклый двойная униформа п-гональный трапецоэдр
Характеристики	выпуклый, вершинно-транзитивный, правильный многоугольник лица
Сеть

В геометрия, п-гональная антипризма или же п-сторонняя антипризма это многогранник состоящий из двух параллельных копий некоторых п-сторонний многоугольник, связанных чередующейся лентой треугольники. Антипризмы - это подкласс призматоиды и являются (вырожденным) типом курносые многогранники.

Антипризмы похожи на призмы за исключением того, что основания скручены относительно друг друга, а боковые грани представляют собой треугольники, а не четырехугольники.

В случае обычного п-сторонней основе обычно рассматривается случай, когда ее копия закручена на угол 180/п градусов. Дополнительная регулярность достигается, когда линия, соединяющая центры основания, перпендикулярна плоскостям основания, что делает ее правая антипризма. Как лица, он имеет два п-гональный базы и, соединяя эти базы, 2п равнобедренные треугольники.

Равномерная антипризма

А униформа антипризма имеет, помимо базовых граней, 2п равносторонние треугольники как грани. Равномерные антипризмы образуют бесконечный класс вершинно-транзитивных многогранников, как и равномерные призмы. За п = 2 у нас есть регулярный тетраэдр как дигональная антипризма (вырожденная антипризма), а для п = 3 регулярный октаэдр как треугольная антипризма (невырожденная антипризма).

Двойные многогранники антипризм трапецоэдры. Их существование обсуждалось, и их название было придумано Иоганн Кеплер, хотя возможно, что они ранее были известны Архимед, поскольку они удовлетворяют тем же условиям на вершинах, что и Архимедовы тела.

Семья униформы п-гональный антипризмы [ v т е ]
Изображение многогранника												...	Апейрогональная антипризма
Сферическое мозаичное изображение												Плоское мозаичное изображение
Конфигурация вершины п.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Диаграммы Шлегеля

A3	A4	A5	A6	A7	A8

Декартовы координаты

Декартовы координаты для вершин правой антипризмы с (правильной) п-угольные основания и равнобедренные треугольники

{displaystyle left (cos {frac {kpi} {n}}, sin {frac {kpi} {n}}, (- 1) ^ {k} hight)}

с k от 0 до 2п - 1; если треугольники равносторонние,

{displaystyle 2h ^ {2} = cos {frac {pi} {n}} - cos {frac {2pi} {n}}.}

Объем и площадь поверхности

Позволять а быть длиной ребра униформа антипризма. Тогда объем

{displaystyle V = {frac {n {sqrt {4cos ^ {2} {frac {pi} {2n}} - 1}} sin {frac {3pi} {2n}}} {12sin ^ {2} {frac {pi } {n}}}} а ^ {3}}

и площадь поверхности

{displaystyle A = {frac {n} {2}} left (cot {frac {pi} {n}} + {sqrt {3}} ight) a ^ {2}.}

Связанные многогранники

Есть бесконечное множество усеченный антипризмы, включая низкосимметричную форму усеченный октаэдр (усеченная треугольная антипризма). Это может быть чередовались создавать пренебрежительные антипризмы, два из которых Твердые тела Джонсона, а курносая треугольная антипризма является формой более низкой симметрии икосаэдр.

Антипризмы
				...
с {2,4}	с {2,6}	с {2,8}	с {2,10}	с {2,2п}
Усеченные антипризмы
				...
ts {2,4}	тс {2,6}	ts {2,8}	тс {2,10}	ts {2,2n}
Курносые антипризмы
J₈₄	Икосаэдр	J₈₅	Неровные лица ...
				...
сс {2,4}	сс {2,6}	сс {2,8}	сс {2,10}	сс {2,2n}

Симметрия

В группа симметрии права п-сторонняя антипризма с правильным основанием и равнобедренными боковыми гранями - D_пd порядка 4п, кроме случая тетраэдр, имеющий большую группу симметрии T_d порядка 24, который имеет три варианта D_2d как подгруппы, так и октаэдр, имеющий большую группу симметрии O_час порядка 48, который имеет четыре версии D_3D как подгруппы.

Группа симметрии содержит инверсия если и только если п странно.

В группа ротации это D_п порядка 2п, за исключением тетраэдра, который имеет большую группу вращения T порядка 12, который имеет три версии D₂ как подгруппы, и октаэдр, который имеет большую группу вращения O порядка 24, который имеет четыре версии D₃ как подгруппы.

Звездная антипризма

5/2-антипризма		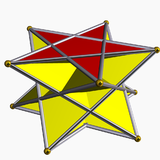	5/3-антипризма
9/2-антипризма		9/4-антипризма		9/5-антипризма

Это показывает все антипризмы, отличные от звезды, и звезды, вплоть до 15 сторон - вместе с таковыми икосикаеннагона.

Однородные звездные антипризмы названы по их звездный многоугольник базы, {п/q}, и существуют в прямом и ретроградном (скрещенном) решениях. Скрещенные формы пересекаются фигуры вершин, и обозначаются обратными дробями, п/(п - q) вместо п/q, например 5/3 вместо 5/2.

В ретроградных формах, но не в прямолинейных, треугольники, соединяющие основания звезд, пересекают ось вращательной симметрии.

Некоторые ретроградные звездные антипризмы с правильными выпуклыми основаниями многоугольника не могут быть построены с равными длинами ребер, поэтому они не являются однородными многогранниками.

Составы звездчатой антипризмы также могут быть построены там, где п и q имеют общие факторы; Пример: звездная антипризма 10/4 представляет собой соединение двух звездчатых антипризм 5/2.

Звездчатые антипризмы по симметрии, до 12
Группа симметрии	Однородные звезды			Другие звезды
D_4d [2⁺,8] (2*5)				3.3/2.3.4
D_5ч [2,5] (*225)	3.3.3.5/2			3.3/2.3.5
D_5d [2⁺,10] (2*5)	3.3.3.5/3
D_6d [2⁺,12] (2*6)		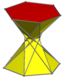		3.3/2.3.6
D_7ч [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
D_7d [2⁺,14] (2*7)	3.3.3.7/3
D_8d [2⁺,16] (2*8)	3.3.3.8/3	3.3.3.8/5
D_9ч [2,9] (*229)	3.3.3.9/2	3.3.3.9/4
D_9d [2⁺,18] (2*9)	3.3.3.9/5
D_10d [2⁺,12] (2*10)	3.3.3.10/3
D_11ч [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
D_11d [2⁺,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
D_12d [2⁺,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...