Правильный многоугольник - Regular polygon

Множество выпуклых правильных n-угольников
Правильные многоугольники
Края и вершины	п
Символ Шлефли	{п}
Диаграмма Кокстера – Дынкина
Группа симметрии	Dп, порядок 2n
Двойной многоугольник	Самодвойственный
Площадь (с длиной стороны, s)	${\displaystyle A={\tfrac {1}{4}}ns^{2}\cot \left({\frac {\pi }{n}}\right)}$
Внутренний угол	${\displaystyle (n-2)\times {\frac {180^{\circ }}{n}}}$
Сумма внутренних углов	${\displaystyle \left(n-2\right)\times 180^{\circ }}$
Диаметр вписанной окружности	${\displaystyle d_{\text{IC}}=s\cot \left({\frac {\pi }{n}}\right)}$
Диаметр описанной окружности	${\displaystyle d_{\text{OC}}=s\csc \left({\frac {\pi }{n}}\right)}$
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В Евклидова геометрия, а правильный многоугольник это многоугольник то есть равносторонний (все углы равны по мере) и равносторонний (все стороны одинаковой длины). Правильные многоугольники могут быть либо выпуклый или же звезда. в предел, последовательность правильных многоугольников с увеличивающимся числом сторон приближает круг, если периметр или же площадь фиксированный, или обычный апейрогон (фактически прямая линия ), если длина ребра фиксированная.

Общие свойства

Правильные выпуклые и звездчатые многоугольники с 3–12 вершинами, помеченные символами Шлефли.

Эти свойства применяются ко всем правильным многоугольникам, выпуклым или выпуклым. звезда.

Обычный п-сторонний многоугольник имеет вращательная симметрия порядка п.

Все вершины правильного многоугольника лежат на общей окружности (точка описанный круг ); т.е. они конциклические точки. То есть правильный многоугольник - это циклический многоугольник.

Вместе со свойством сторон равной длины это означает, что каждый правильный многоугольник также имеет вписанную окружность или окружать это касается каждой стороны в средней точке. Таким образом, правильный многоугольник - это касательный многоугольник.

Обычный п-сторонний многоугольник может быть построен с компас и линейка если и только если странный основной факторы п отличны Простые числа Ферма. Видеть конструктивный многоугольник.

Симметрия

В группа симметрии из п-сторонний правильный многоугольник группа диэдра D_п (порядка 2п): D₂, D₃, D₄, ... Он состоит из вращений в C_п, вместе с симметрия отражения в п оси, проходящие через центр. Если п даже тогда половина этих осей проходит через две противоположные вершины, а другая половина - через середины противоположных сторон. Если п нечетно, то все оси проходят через вершину и середину противоположной стороны.

Правильные выпуклые многоугольники

Все обычные простые многоугольники (простой многоугольник - это такой, который нигде не пересекает себя) выпуклые. Те, у кого одинаковое количество сторон, также похожий.

An п-сторонний выпуклый правильный многоугольник обозначается его Символ Шлефли {п}. За п <3, имеем два выродиться случаи:

Моногон {1}

Вырождаться в обычное пространство. (Большинство авторитетов не рассматривают моногон как истинный многоугольник, отчасти из-за этого, а также из-за того, что приведенные ниже формулы не работают, а его структура не соответствует ни одной абстрактный многоугольник.)

Дигон {2}; "двойной отрезок"

Вырождаться в обычное пространство. (Из-за этого некоторые авторитеты не считают двуугольник настоящим многоугольником.)

В определенных контекстах все рассматриваемые полигоны будут правильными. В таких условиях приставка обычная принято опускать. Например, все лица равномерные многогранники должны быть правильными, а грани будут описаны просто как треугольник, квадрат, пятиугольник и т. д.

Углы

Для правильной выпуклой п-угольник, каждый внутренний угол имеет размер:

${\displaystyle {\frac {180(n-2)}{n}}}$ градусы;

${\displaystyle {\frac {(n-2)\pi }{n}}}$ радианы; или же

${\displaystyle {\frac {(n-2)}{2n}}}$ полный повороты,

и каждый внешний угол (т.е. дополнительный к внутреннему углу) имеет меру ${\displaystyle {\tfrac {360}{n}}}$ градусов, при этом сумма внешних углов равна 360 градусам или 2π радианам или одному полному обороту.

Поскольку количество сторон n приближается к бесконечности, внутренний угол приближается к 180 градусам. Для правильного многоугольника с 10000 сторон (a мириагон ) внутренний угол составляет 179,964 °. По мере увеличения количества сторон внутренний угол может приближаться к 180 °, а форма многоугольника приближается к форме круга. Однако многоугольник никогда не может стать кругом. Значение внутреннего угла никогда не может стать точно равным 180 °, поскольку окружность фактически превратилась бы в прямую линию. По этой причине круг - это не многоугольник с бесконечным числом сторон.

Диагонали

За п > 2, количество диагонали является ${\displaystyle {\tfrac {1}{2}}n(n-3)}$; то есть 0, 2, 5, 9, ..., для треугольника, квадрата, пятиугольника, шестиугольника, .... Диагонали делят многоугольник на 1, 4, 11, 24, ... части. OEIS: A007678.

Для регулярного п-угольник, вписанный в окружность единичного радиуса, произведение расстояний от данной вершины до всех других вершин (включая соседние вершины и вершины, соединенные диагональю) равно п.

Очки в плоскости

Для обычного простого п-гон с по окружности р и расстояния d_я из произвольной точки на плоскости к вершинам имеем^[1]

${\displaystyle {\frac {\sum _{i=1}^{n}d_{i}^{4}}{n}}+3R^{4}=\left({\frac {\sum _{i=1}^{n}d_{i}^{2}}{n}}+R^{2}\right)^{2}.}$

Для больших расстояний ${\displaystyle d_{i}}$ из произвольной точки на плоскости в вершины правильного ${\displaystyle n}$-угольник, если

${\displaystyle S_{n}^{(2m)}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2m}}$,

тогда^[2]

${\displaystyle S_{n}^{(2m)}=(S_{n}^{(2)})^{m}+\sum _{k=1}^{\lfloor {\frac {m}{2}}\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R^{2k}(S_{n}^{(2)}-R^{2})^{k}(S_{n}^{(2)})^{m-2k}}$,

и

${\displaystyle S_{n}^{(2m)}=(S_{n}^{(2)})^{m}+\sum _{k=1}^{\lfloor {\frac {m}{2}}\rfloor }{\frac {1}{2^{k}}}{\binom {m}{2k}}{\binom {2k}{k}}(S_{n}^{(4)}-(S_{n}^{(2)})^{2})^{k}(S_{n}^{(2)})^{m-2k}}$,

куда ${\displaystyle m}$ положительное целое число меньше, чем ${\displaystyle n}$.

Если ${\displaystyle L}$ - расстояние от произвольной точки на плоскости до центра тяжести правильного ${\displaystyle n}$-угольник с радиусом описанной окружности ${\displaystyle R}$, тогда ^[2]

${\displaystyle \sum _{i=1}^{n}d_{i}^{2m}=n((R^{2}+L^{2})^{m}+\sum _{k=1}^{\lfloor {\frac {m}{2}}\rfloor }{\binom {m}{2k}}{\binom {2k}{k}}R^{2k}L^{2k}(R^{2}+L^{2})^{m-2k})}$,

куда ${\displaystyle m}$ = 1,2,…, ${\displaystyle n}$ -1.

Внутренние точки

Для регулярного п-угольник, сумма перпендикулярных расстояний от любой внутренней точки до п стороны п раз апофема^{[3]:п. 72} (апофема - это расстояние от центра до любой стороны). Это обобщение Теорема Вивиани для п= 3 случая.^[4][5]

Circumradius

Обычный пятиугольник (п = 5) с сторона s, по окружности р и апофема а

Графики сторона, s ; апофема, а и площадь, А из правильные многоугольники из п стороны и по окружности 1, с основание, б из прямоугольник с такой же площадью - зеленая линия показывает корпус п = 6

В по окружности р от центра правильного многоугольника до одной из вершин зависит от длины стороны s или в апофема а к

${\displaystyle R={\frac {s}{2\sin \left({\frac {\pi }{n}}\right)}}={\frac {a}{\cos \left({\frac {\pi }{n}}\right)}}}$

За конструктивные многоугольники, алгебраические выражения ибо эти отношения существуют; видеть Бицентрический многоугольник # Правильные многоугольники.

Сумма перпендикуляров от правильного п-угольника к любой прямой, касающейся описанной окружности, равно п умноженное на радиус описанной окружности.^{[3]:п. 73}

Сумма квадратов расстояний от вершин правильного п-угольник в любую точку его описанной окружности равно 2nR² куда р это радиус описанной окружности.^{[3]:стр.73}

Сумма квадратов расстояний от середин сторон правильного п-угольник в любую точку описанной окружности равен 2nR² − нс²/4, куда s это длина стороны и р это радиус описанной окружности.^{[3]:п. 73}

Если ${\displaystyle d_{i}}$ - расстояния от вершин правильного ${\displaystyle n}$-угольник в любую точку описанной окружности, тогда ^[2]

${\displaystyle 3(\sum _{i=1}^{n}d_{i}^{2})^{2}=2n\sum _{i=1}^{n}d_{i}^{4}}$.

Расслоения

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на ${\displaystyle {\tbinom {n}{2}}}$ или же м(м-1) / 2 параллелограмма. Эти мозаики содержатся в виде подмножеств вершин, ребер и граней в ортогональных проекциях. м-кубы.^[6]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. OEIS: A006245 дает количество решений для меньших полигонов.

Пример сечения для выбранных правильных четных многоугольников

2м	6	8	10	12	14	16	18	20	24	30	40	50
Изображение
Ромбы	3	6	10	15	21	28	36	45	66	105	190	300

Площадь

Площадь А выпуклой регулярной п-сторонний многоугольник, имеющий сторона s, по окружности р, апофема а, и периметр п дан кем-то^[7][8]

${\displaystyle A={\tfrac {1}{2}}nsa={\tfrac {1}{2}}pa={\tfrac {1}{4}}ns^{2}\cot \left({\tfrac {\pi }{n}}\right)=na^{2}\tan \left({\tfrac {\pi }{n}}\right)={\tfrac {1}{2}}nR^{2}\sin \left({\tfrac {2\pi }{n}}\right)}$

Для правильных многоугольников со стороной s = 1, радиус описанной окружности р = 1, или апофема а = 1, получается следующая таблица:^[9] (Обратите внимание, что поскольку ${\displaystyle \cot x\rightarrow 1/x}$ в качестве ${\displaystyle x\rightarrow 0}$,^[10] область, когда ${\displaystyle s=1}$ стремится к ${\displaystyle n^{2}/4\pi }$ в качестве ${\displaystyle n}$ становится большим.)

Число сторон	Площадь, когда сбоку s = 1		Площадь окружности радиуса р = 1			Площадь при апофеме а = 1
	Точный	Приближение	Точный	Приближение	В качестве (приблизительного) доля описанный круг площадь	Точный	Приближение	В качестве (приблизительного) несколько из  окружать площадь
п	${\displaystyle {\tfrac {n}{4}}\cot \left({\tfrac {\pi }{n}}\right)}$		${\displaystyle {\tfrac {n}{2}}\sin \left({\tfrac {2\pi }{n}}\right)}$		${\displaystyle {\tfrac {n}{2\pi }}\sin \left({\tfrac {2\pi }{n}}\right)}$	${\displaystyle n\tan \left({\tfrac {\pi }{n}}\right)}$		${\displaystyle {\tfrac {n}{\pi }}\tan \left({\tfrac {\pi }{n}}\right)}$
3	${\displaystyle {\tfrac {\sqrt {3}}{4}}}$	0.433012702	${\displaystyle {\tfrac {3{\sqrt {3}}}{4}}}$	1.299038105	0.4134966714	${\displaystyle 3{\sqrt {3}}}$	5.196152424	1.653986686
4	1	1.000000000	2	2.000000000	0.6366197722	4	4.000000000	1.273239544
5	${\displaystyle {\tfrac {1}{4}}{\sqrt {25+10{\sqrt {5}}}}}$	1.720477401	${\displaystyle {\tfrac {5}{4}}{\sqrt {{\tfrac {1}{2}}\left(5+{\sqrt {5}}\right)}}}$	2.377641291	0.7568267288	${\displaystyle 5{\sqrt {5-2{\sqrt {5}}}}}$	3.632712640	1.156328347
6	${\displaystyle {\tfrac {3{\sqrt {3}}}{2}}}$	2.598076211	${\displaystyle {\tfrac {3{\sqrt {3}}}{2}}}$	2.598076211	0.8269933428	${\displaystyle 2{\sqrt {3}}}$	3.464101616	1.102657791
7		3.633912444		2.736410189	0.8710264157		3.371022333	1.073029735
8	${\displaystyle 2+2{\sqrt {2}}}$	4.828427125	${\displaystyle 2{\sqrt {2}}}$	2.828427125	0.9003163160	${\displaystyle 8\left({\sqrt {2}}-1\right)}$	3.313708500	1.054786175
9		6.181824194		2.892544244	0.9207254290		3.275732109	1.042697914
10	${\displaystyle {\tfrac {5}{2}}{\sqrt {5+2{\sqrt {5}}}}}$	7.694208843	${\displaystyle {\tfrac {5}{2}}{\sqrt {{\tfrac {1}{2}}\left(5-{\sqrt {5}}\right)}}}$	2.938926262	0.9354892840	${\displaystyle 2{\sqrt {25-10{\sqrt {5}}}}}$	3.249196963	1.034251515
11		9.365639907		2.973524496	0.9465022440		3.229891423	1.028106371
12	${\displaystyle 6+3{\sqrt {3}}}$	11.19615242	3	3.000000000	0.9549296586	${\displaystyle 12\left(2-{\sqrt {3}}\right)}$	3.215390309	1.023490523
13		13.18576833		3.020700617	0.9615188694		3.204212220	1.019932427
14		15.33450194		3.037186175	0.9667663859		3.195408642	1.017130161
15	[11]	17.64236291	[12]	3.050524822	0.9710122088	[13]	3.188348426	1.014882824
16	[14]	20.10935797	${\displaystyle 4{\sqrt {2-{\sqrt {2}}}}}$	3.061467460	0.9744953584	[15]	3.182597878	1.013052368
17		22.73549190		3.070554163	0.9773877456		3.177850752	1.011541311
18		25.52076819		3.078181290	0.9798155361		3.173885653	1.010279181
19		28.46518943		3.084644958	0.9818729854		3.170539238	1.009213984
20	[16]	31.56875757	[17]	3.090169944	0.9836316430	[18]	3.167688806	1.008306663
100		795.5128988		3.139525977	0.9993421565		3.142626605	1.000329117
1000		79577.20975		3.141571983	0.9999934200		3.141602989	1.000003290
10,000		7957746.893		3.141592448	0.9999999345		3.141592757	1.000000033
1,000,000		79577471545		3.141592654	1.000000000		3.141592654	1.000000000

Сравнение размеров правильных многоугольников с одинаковой длиной ребра, от три к шестьдесят стороны. Размер неограниченно увеличивается по мере приближения числа сторон к бесконечности.

Из всех п-угольники с заданным периметром, тот, у которого наибольшая площадь, правильный.^[19]

Конструируемый многоугольник

Основная статья: Конструируемый многоугольник

Некоторые правильные многоугольники легко строить с циркулем и линейкой; другие правильные многоугольники вообще невозможно построить. древнегреческие математики умел построить правильный многоугольник с 3, 4 или 5 сторонами,^{[20]:п. xi} и они знали, как построить правильный многоугольник с удвоенным числом сторон данного правильного многоугольника.^{[20]:стр. 49–50} В связи с этим возник вопрос: можно ли построить все обычный п-угольники с циркулем и линейкой? Если нет, то какой п-угольники можно построить, а какие нет?

Карл Фридрих Гаусс доказал конструктивность регулярного 17-угольник в 1796 году. Пятью годами позже он разработал теорию Гауссовские периоды в его Disquisitiones Arithmeticae. Эта теория позволила ему сформулировать достаточное условие для конструктивности правильных многоугольников:

Обычный п-угольник можно построить с помощью циркуля и линейки, если п является произведением степени двойки и любого количества различных Простые числа Ферма (в том числе ни одного).

(Простое число Ферма - это простое число формы ${\displaystyle 2^{(2^{n})}+1.}$) Гаусс без доказательства заявил, что это условие также необходимо, но никогда не публиковал свое доказательство. Полное доказательство необходимости было предоставлено Пьер Ванцель в 1837 году. Результат известен как Теорема Гаусса – Вантцеля..

Эквивалентно обычный п-gon можно построить тогда и только тогда, когда косинус ее общего угла - это конструктивное число - то есть может быть записано в терминах четырех основных арифметических операций и извлечения квадратных корней.

Правильные косые многоугольники

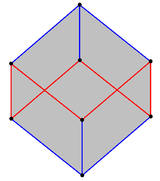В куб содержит перекос регулярный шестиугольник, видно как 6 красных краев, зигзагообразных между двумя плоскостями, перпендикулярными диагональной оси куба.

Зигзагообразные боковые края п-антипризма представляют собой правильный перекос 2п-угольник, как показано на этой 17-угольной антипризме.

А обычный наклонный многоугольник в 3-м пространстве можно рассматривать как неплоские пути, зигзагообразные между двумя параллельными плоскостями, определяемые как боковые края однородной антипризма. Все края и внутренние углы равны.

В Платоновы тела (в тетраэдр, куб, октаэдр, додекаэдр, и икосаэдр ) имеют многоугольники Петри, показанные здесь красным, со сторонами 4, 6, 6, 10 и 10 соответственно.

В более общем смысле правильные косые многоугольники можно определить в п-Космос. Примеры включают Полигоны Петри, многоугольные пути ребер, разделяющих правильный многогранник на две половины и выглядит как правильный многоугольник в ортогональной проекции.

В бесконечном пределе правильные косые многоугольники стать перекосом апейрогоны.

Правильные звездчатые многоугольники

Правильные звездчатые многоугольники

2 <2q gcd (p, q) = 1 {5/2} {7/2} {7/3}...
Символ Шлефли	{p / q}
Вершины и Края	п
Плотность	q
Диаграмма Кокстера
Группа симметрии	Двугранный (Dп)
Двойной многоугольник	Самодвойственный
Внутренний угол (градусы )	${\displaystyle {\frac {180(p-2q)}{p}}}$[21]

Невыпуклый правильный многоугольник - это правильный звездный многоугольник. Самый распространенный пример - это пентаграмма, имеющая те же вершины, что и пятиугольник, но соединяет чередующиеся вершины.

Для п-сторонний звездный многоугольник Символ Шлефли изменен, чтобы указать плотность или "звездность" м многоугольника, как {п/м}. Если м равно 2, например, каждая вторая точка присоединяется. Если м равно 3, то присоединяется каждая третья точка. Граница многоугольника огибает центр м раз.

(Невырожденные) правильные звезды с числом сторон до 12:

• Пентаграмма – {5/2}
• Гептаграмма - {7/2} и {7/3}
• Октаграмма – {8/3}
• Эннеаграмма - {9/2} и {9/4}
• Декаграмма – {10/3}
• Хендекаграмма - {11/2}, {11/3}, {11/4} и {11/5}
• Додекаграмма – {12/5}

м и п должно быть совмещать, иначе фигура выродится.

Вырожденные правильные звезды с числом сторон до 12:

• Тетрагон - {4/2}
• Шестиугольники - {6/2}, {6/3}
• Октагоны - {8/2}, {8/4}
• Эннеагон - {9/3}
• Декагоны - {10/2}, {10/4} и {10/5}
• Додекагоны - {12/2}, {12/3}, {12/4} и {12/6}

Две интерпретации {6/2}

Грюнбаум {6/2} или 2 {3}[22]	Coxeter 2{3} или {6} [2 {3}] {6}
Шестигранник с двойной обмоткой	Гексаграмма как соединение двух треугольников

В зависимости от точного происхождения символа Шлефли мнения разнятся относительно природы вырожденной фигуры. Например, {6/2} можно лечить одним из двух способов:

• На протяжении большей части 20-го века (см., Например, Кокстер (1948) ), мы обычно использовали / 2 для обозначения соединения каждой вершины выпуклого {6} с ее ближайшими соседями на расстоянии двух шагов, чтобы получить регулярный сложный двух треугольников, или гексаграмма.
  Кокстер поясняет это обычное соединение с помощью обозначения {kp} [k {p}] {kp} для соединения {p / k}, поэтому гексаграмма представлен как {6} [2 {3}] {6}.^[23] Более компактно Кокстер также пишет 2{n / 2}, нравится 2{3} для гексаграммы составной как чередования правильных четных многоугольников с курсивом по ведущему фактору, чтобы отличить его от совпадающей интерпретации.^[24]
• Многие современные геометры, такие как Грюнбаум (2003),^[22] считаю это неправильным. Они используют / 2 для обозначения перемещения на два места вокруг {6} на каждом шаге, получая треугольник "с двойной обмоткой", у которого две вершины наложены друг на друга в каждой угловой точке и два ребра вдоль каждого сегмента линии. Это не только лучше согласуется с современными теориями абстрактные многогранники, но он также более точно копирует способ, которым Пуансо (1809) создал свои звездные многоугольники - взяв один отрезок проволоки и согнув его в последовательных точках под тем же углом, пока фигура не сомкнется.

Двойственность правильных многоугольников

Смотрите также: Самодвойственные многогранники

Все правильные многоугольники самодвойственны для конгруэнтности, а для нечетных п они самодвойственны идентичности.

Кроме того, правильные звездные фигуры (соединения), состоящие из правильных многоугольников, также самодуальны.

Правильные многоугольники как грани многогранников

А равномерный многогранник имеет правильные многоугольники как грани, так что для каждых двух вершин существует изометрия отображение одного в другой (точно так же, как для правильного многоугольника).

А квазирегулярный многогранник представляет собой равномерный многогранник, у каждой вершины которого чередуются грани двух типов.

А правильный многогранник представляет собой равномерный многогранник с одной гранью.

Остальные (неоднородные) выпуклые многогранники с правильными лицами известны как Твердые тела Джонсона.

Многогранник с правильными треугольниками гранями называется многогранником. дельтаэдр.

Смотрите также

• Евклидовы мозаики выпуклыми правильными многоугольниками
• Платоново твердое тело
• Апейрогон - Многоугольник с бесконечными сторонами также может быть правильным, {∞}.
• Список правильных многогранников и соединений
• Равносторонний многоугольник
• Карлайл круг

Примечания

1. Парк, Пу-Сун. "Расстояния регулярных многогранников", Форум Geometricorum 16, 2016, 227-232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
2. Месхишвили, Мамука (2020). «Средние циклические правильные многоугольники и платоновы тела». Коммуникации в математике и приложениях. 11: 335–355.
3. Джонсон, Роджер А., Продвинутая евклидова геометрия, Dover Publ., 2007 (ориг. 1929 г.).
4. Пиковер, Клиффорд А, Книга по математике, Стерлинг, 2009: с. 150
5. Чен, Чжибо, и Лян, Тянь. «Обратное к теореме Вивиани», Математический журнал колледжа 37 (5), 2006, стр. 390–391.
6. Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
7. «Открытый справочник по математике». Получено 4 февраля 2014.
8. "Математические слова".
9. Результаты для р = 1 и а = 1, полученное с помощью Клен, используя определение функции:

   ж := proc (п)опции оператор, стрелка;[ [конвертировать(1/4*п*детская кроватка(число Пи/п), радикальный), конвертировать(1/4*п*детская кроватка(число Пи/п), плавать)], [конвертировать(1/2*п*грех(2*число Пи/п), радикальный), конвертировать(1/2*п*грех(2*число Пи/п), плавать), конвертировать(1/2*п*грех(2*число Пи/п)/число Пи, плавать)], [конвертировать(п*загар(число Пи/п), радикальный), конвертировать(п*загар(число Пи/п), плавать), конвертировать(п*загар(число Пи/п)/число Пи, плавать)]]конец proc

   Выражения для п= 16 получаются двойным применением формула касательного полуугла загорать (π / 4)

10. Тригонометрические функции
11. ${\displaystyle {\tfrac {15}{8}}\left({\sqrt {15}}+{\sqrt {3}}+{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right)}$
12. ${\displaystyle {\tfrac {15}{16}}\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)}$
13. ${\displaystyle {\tfrac {15}{2}}\left(3{\sqrt {3}}-{\sqrt {15}}-{\sqrt {2\left(25-11{\sqrt {5}}\right)}}\right)}$
14. ${\displaystyle 4\left(1+{\sqrt {2}}+{\sqrt {2\left(2+{\sqrt {2}}\right)}}\right)}$
15. ${\displaystyle 16\left(1+{\sqrt {2}}\right)\left({\sqrt {2\left(2-{\sqrt {2}}\right)}}-1\right)}$
16. ${\displaystyle 5\left(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {5}}}}\right)}$
17. ${\displaystyle {\tfrac {5}{2}}\left({\sqrt {5}}-1\right)}$
18. ${\displaystyle 20\left(1+{\sqrt {5}}-{\sqrt {5+2{\sqrt {5}}}}\right)}$
19. Чакериан Г.Д. "Искаженное представление о геометрии". Гл. 7 дюйм Математические сливы (Р. Хонсбергер, редактор). Вашингтон, округ Колумбия: Математическая ассоциация Америки, 1979: 147.
20. Смелый, Бенджамин. Известные задачи геометрии и способы их решения, Dover Publications, 1982 (начало 1969 г.).
21. Каппрафф, Джей (2002). За гранью: экскурсия по природе, мифам и числам. World Scientific. п. 258. ISBN  978-981-02-4702-7.
22. Ваши многогранники такие же, как мои многогранники? Бранко Грюнбаум (2003), рис.
23. Правильные многогранники, стр.95
24. Кокстер, Плотности правильных многогранников, II, 1932, стр.53.

Рекомендации

• Кокстер, H.S.M. (1948). «Правильные многогранники». Метуэн и Ко.
• Grünbaum, B .; Ваши многогранники такие же, как мои многогранники ?, Дискретный и вычислительный. geom: фестиваль Гудмана-Поллака, Ред. Аронов и др., Springer (2003), стр. 461–488.
• Пуансо, Л.; Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9 (1810), стр. 16–48.

внешняя ссылка

• Вайсштейн, Эрик В. "Правильный многоугольник". MathWorld.
• Описание регулярного многоугольника С интерактивной анимацией
• Вписанная окружность правильного многоугольника С интерактивной анимацией
• Площадь правильного многоугольника Три разные формулы с интерактивной анимацией
• Построения правильных многоугольников художниками эпохи Возрождения в Конвергенция

Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	Ап	Bп	я2(п) / Dп	E6 / E7 / E8 / F4 / грамм2	ЧАСп
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукруглый	132 • 231 • 321
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	142 • 241 • 421
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукруглый
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1k2 • 2k1 • k21	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений