Правильный додекаэдр - Regular dodecahedron

Правильный додекаэдр
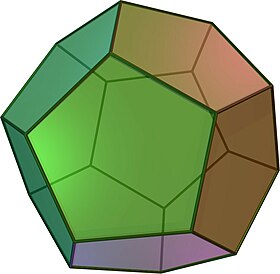(Нажмите здесь, чтобы повернуть модель)
Тип	Платоново твердое тело
Элементы	F = 12, E = 30 V = 20 (χ = 2)
Лица по сторонам	12{5}
Обозначение Конвея	D
Символы Шлефли	{5,3}
Конфигурация лица	V3.3.3.3.3
Символ Wythoff	3 | 2 5
Диаграмма Кокстера
Симметрия	ячас, H3, [5,3], (*532)
Группа вращения	я, [5,3]^+, (532)
Рекомендации	U23, C26, W5
Характеристики	обычный, выпуклый
Двугранный угол	116,56505 ° = arccos (-^1⁄√5)
5.5.5 (Фигура вершины )	Правильный икосаэдр (двойственный многогранник )
Сеть

Анимация складывания сетки правильного (пятиугольного) додекаэдра

3D модель правильного додекаэдра

А правильный додекаэдр или же пятиугольный додекаэдр это додекаэдр то есть обычный, который состоит из 12 обычный пятиугольник лица, по три встречи на каждом вершина. Это один из пяти Платоновы тела. У него 12 граней, 20 вершин, 30 ребер и 160 диагоналей (60 диагонали лица, 100 диагонали пространства ).^[1] Он представлен Символ Шлефли {5,3}.

Размеры

Если длина ребра правильного додекаэдра равна «${\displaystyle a}$”, радиус из ограниченная сфера (тот, который касается правильного додекаэдра во всех вершинах)

${\displaystyle r_{u}=a{\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\approx 1.401\,258\,538\cdot a}$ OEIS: A179296

и радиус вписанной сферы (касательная каждой из граней правильного додекаэдра)

${\displaystyle r_{i}=a{\frac {1}{2}}{\sqrt {{\frac {5}{2}}+{\frac {11}{10}}{\sqrt {5}}}}\approx 1.113\,516\,364\cdot a}$

в то время как средний радиус, который касается середины каждого края, равен

${\displaystyle r_{m}=a{\frac {1}{4}}\left(3+{\sqrt {5}}\right)\approx 1.309\,016\,994\cdot a}$

Эти количества также могут быть выражены как

${\displaystyle r_{u}=a\,{\frac {\sqrt {3}}{2}}\phi }$

${\displaystyle r_{i}=a\,{\frac {\phi ^{2}}{2{\sqrt {3-\phi }}}}}$

${\displaystyle r_{m}=a\,{\frac {\phi ^{2}}{2}}}$

куда ϕ это Золотое сечение.

Отметим, что для правильного додекаэдра с длиной ребра один, р_ты - радиус описывающей сферы вокруг куб длины кромки ϕ, и р_я это апофема правильного пятиугольника с длиной ребра ϕ.

Площадь и объем поверхности

В площадь поверхности А и объем V правильного додекаэдра реберной длины а находятся:

${\displaystyle {\displaystyle A=3{\sqrt {25+10{\sqrt {5}}}}a^{2}\approx 20.645\,728\,807a^{2}}}$

${\displaystyle V={\frac {1}{4}}(15+7{\sqrt {5}})a^{3}\approx 7.663\,118\,9606a^{3}}$

Кроме того, площадь поверхности и объем правильного додекаэдра связаны с величиной Золотое сечение. Додекаэдр с длиной ребра в одну единицу обладает свойствами:^[2]

${\displaystyle {\displaystyle A={\frac {15\varphi }{\sqrt {3-\varphi }}}}}$

${\displaystyle {\displaystyle V={\frac {5\varphi ^{3}}{6-2\varphi }}}}$

Двумерные проекции симметрии

В правильный додекаэдр имеет два специальных ортогональные проекции, по центру, на вершины и пятиугольные грани, соответствуют A₂ и H₂ Самолеты Кокстера.

Ортогональные проекции

В центре	Вершина	Край	Лицо
Изображение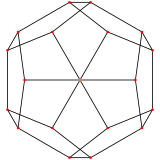
Проективный симметрия	[[3]] = [6]	[2]	[[5]] = [10]

В перспективная проекция Если смотреть на пятиугольную грань, правильный додекаэдр можно рассматривать как прямолинейный Диаграмма Шлегеля, или же стереографическая проекция как сферический многогранник. Эти проекции также используются для отображения четырехмерного 120 ячеек, правильный 4-мерный многогранник, построенный из 120 додекаэдров, проецируя его до 3-х измерений.

Проекция	Ортогональная проекция	Перспективная проекция
		Диаграмма Шлегеля	Стереографическая проекция
Правильный додекаэдр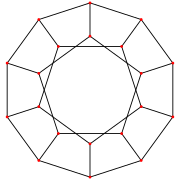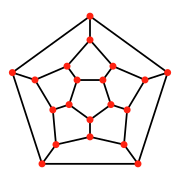
Додекаплекс (120 ячеек )

Сферическая черепица

Правильный додекаэдр также можно представить в виде сферическая черепица.

Ортографическая проекция	Стереографическая проекция

Декартовы координаты

Координаты вершины:
	Оранжевые вершины лежат в точках (± 1, ± 1, ± 1) и образуют куб (пунктирные линии).
	Зеленые вершины лежат в точках (0, ±ϕ, ±1/ϕ) и сформируйте прямоугольник на yz-самолет.
	Синие вершины лежат в точках (±1/ϕ, 0, ±ϕ) и сформируйте прямоугольник на xz-самолет.
	Розовые вершины лежат в точках (±ϕ, ±1/ϕ, 0) и образуют прямоугольник на ху-самолет.
Расстояние между соседними вершинами равно 2/ϕ, а расстояние от начала координат до любой вершины равно √3. ϕ = 1 + √5/2 это золотое сечение.

Следующее Декартовы координаты определите 20 вершин правильного додекаэдра с центром в начале координат, соответствующим масштабом и ориентацией:^[3]

(±1, ±1, ±1)

(0, ±ϕ, ±1/ϕ)

(±1/ϕ, 0, ±ϕ)

(±ϕ, ±1/ϕ, 0)

куда ϕ = 1 + √5/2 это Золотое сечение (также написано τ) ≈ 1,618. Длина кромки 2/ϕ = √5 − 1. В по окружности является√3.

Уравнения, определяющие грань

Подобно симметрии координат вершин, уравнения двенадцати граней правильного додекаэдра также демонстрируют симметрию своих коэффициентов:

Икс ± ϕy = ±ϕ²

у ± ϕz = ±ϕ²

z ± ϕx = ±ϕ²

Характеристики

• В двугранный угол правильного додекаэдра равно 2арктан (ϕ) или примерно 116.565° (где снова ϕ = 1 + √5/2, то Золотое сечение ). OEIS: A137218 Обратите внимание, что тангенс двугранного угла точно равен −2.
• Если исходный правильный додекаэдр имеет длину ребра 1, его двойственный икосаэдр имеет длину края ϕ.
• Если пять Платоновых тел имеют одинаковый объем, правильный додекаэдр имеет самые короткие края.
• Имеет 43380 сети.
• Число раскраски карты граней правильного додекаэдра равно 4.
• Расстояние между вершинами одной грани, не связанными ребром, равно ϕ умножить на длину края.
• Если два ребра имеют общую вершину, то середины этих ребер образуют треугольник 36-72-72 с центром тела.

Геометрические отношения

В правильный додекаэдр является третьим в бесконечном наборе усеченные трапецоэдры который может быть построен путем усечения двух осевых вершин пятиугольный трапецоэдр.

В звездчатые правильного додекаэдра составляют три из четырех Многогранники Кеплера – Пуансо.

А исправленный правильный додекаэдр образует икосододекаэдр.

Правильный додекаэдр имеет икосаэдрическая симметрия я_час, Группа Кокстера [5,3], порядок 120, с абстрактной групповой структурой А₅ × Z₂.

Отношение к правильному икосаэдру

Когда правильный додекаэдр вписан в сфера, он занимает больше объема сферы (66,49%), чем икосаэдр, вписанный в ту же сферу (60,55%).

Правильный додекаэдр с длиной ребра 1 имеет более чем в три с половиной раза объем икосаэдра с такой же длиной ребер (7,663 ... по сравнению с 2,181 ...), что примерно составляет 3.51246117975, или точнее: 3/5(3ϕ + 1) или же (1.8ϕ + 0.6).

У правильного додекаэдра 12 граней и 20 вершин, а у правильного икосаэдра 20 граней и 12 вершин. У обоих по 30 ребер.

Отношение к вложенному кубу

Куб может быть встроен в правильный додекаэдр, прикрепленный к восьми из его равноудаленных вершин в пяти различных положениях.^[4] Фактически, пять кубов могут перекрываться и блокироваться внутри правильного додекаэдра, что приводит к соединение пяти кубиков.

Отношение ребра правильного додекаэдра к ребру куба, вложенного внутрь такого правильного додекаэдра, равно 1:ϕ, или же (ϕ − 1) : 1.

Отношение объема правильного додекаэдра к объему куба, заключенного в такой правильный додекаэдр, равно 1:2/2 + ϕ, или же 1 + ϕ/2 : 1 или (5 +√5) : 4.

Например, встроенный куб объемом 64 (и длиной ребра 4) будет вложен в правильный додекаэдр объемом 64 + 32.ϕ (и длина кромки 4ϕ − 4).

Таким образом, разница в объеме между окружающим правильным додекаэдром и замкнутым кубом всегда составляет половину объема куба, умноженного наϕ.

Из этих соотношений выводятся простые формулы для объема правильного додекаэдра с длиной ребра а по золотой середине:

V = (aϕ)³ · 1/4(5 + √5)

V = 1/4(14ϕ + 8)а³

Отношение к золотому прямоугольнику

Золотые прямоугольники отношения (ϕ + 1): 1 и ϕ : 1 также идеально вписывается в правильный додекаэдр.^[5] Пропорционально этому золотому прямоугольнику край замкнутого куба равен ϕ, когда большая длина прямоугольника равна ϕ + 1 (или ϕ²), а короткая длина равна 1 (общее ребро с правильным додекаэдром).

Кроме того, в центре каждой грани правильного додекаэдра образуют три пересекающихся золотых прямоугольника.^[6]

Связь с 6-кубом и ромбическим триаконтаэдром

Проекция 6-полукуба на правильную додекаэдрическую огибающую

Его можно проецировать в 3D из 6-мерного 6-полукуб используя те же базисные векторы, которые образуют оболочку ромбический триаконтаэдр от 6-куб. Здесь показаны 12 внутренних вершин, которые не соединены внешними краями корпуса стандартной длины 6D. √2, сформировать правильный икосаэдр.

Базисные векторы трехмерной проекции [ты,v,ш] используются:

ты = (1, φ, 0, -1, φ, 0)

v = (φ, 0, 1, φ, 0, -1)

ш = (0, 1, φ, 0, -1, φ)

История и использование

Римский додекаэдр

Всенаправленный источник звука

Обычные додекаэдрические объекты нашли практическое применение, а также сыграли роль в изобразительном искусстве и философии.

Ямблих утверждает, что Гиппас, пифагорейец, погиб в море, потому что хвастался, что впервые открыл «сферу с двенадцатью пятиугольниками».^[7] В Theaetetus, диалог Платона, Платон смог доказать, что существует всего пять однородных правильных тел; позже они стали известны как платоновые тела. Тимей (ок. 360 г. до н. э.), как персонаж диалога Платона, связывает другие четыре платоновых тела с четырьмя классические элементы, добавив, что существует пятый сплошной узор, который, хотя обычно ассоциируется с правильным додекаэдром, никогда прямо не упоминается как таковой; «Этого Бог использовал при описании Вселенной».^[8] Аристотель также постулировал, что небеса состоят из пятого элемента, который он назвал aithêr (эфир на латыни, эфир на американском английском).

Обычные додекаэдры использовались как игральные кости и, вероятно, также как гадательные приспособления. Вовремя Эллинистическая эпоха, малая, полая бронза Римский додекаэдр были сделаны и были найдены в различных римских руинах в Европе. Их цель не ясна.

В Искусство 20 века, додекаэдры появляются в работе М. К. Эшер, например, его литографии Рептилии (1943) и Гравитация (1952). В Сальвадор Дали картина Таинство Тайной вечери (1955) помещение представляет собой полый правильный додекаэдр. Жерар Карис Основал все свое художественное творчество на правильном додекаэдре и пятиугольнике, который представлен как новое направление в искусстве, названное пентагонизмом.

Стена для скалолазания, состоящая из трех додекаэдров

В современном ролевые игры, правильный додекаэдр часто используется как двенадцатигранный кубик, один из наиболее распространенных многогранная игральная кость.

Иммерсивные СМИ Компания-производитель камер создала камеру Dodeca 2360, первую в мире камеру с полным движением на 360 °, которая снимает видео высокого разрешения со всех сторон одновременно со скоростью более 100 миллионов пикселей в секунду или 30 кадров в секунду.^{[рекламный язык ]} Он основан на правильном додекаэдре.^{[нужна цитата ]}

В Мегаминкс извилистая головоломка, наряду со своими аналогами большего и меньшего порядка, имеет форму правильного додекаэдра.

В детском романе Фантомная переговорная будка, правильный додекаэдр появляется как символ в стране математики. Каждое его лицо имеет различное выражение - например счастливый, сердитый, грустный - который он поворачивает вперед, чтобы соответствовать своему настроению.

В природе

Ископаемое кокколитофора

Ho-Mg-Zn квазикристалл

Ископаемое кокколитофора Braarudosphaera bigelowii (см. рисунок), одноклеточный прибрежный фитопланктонный водоросль, имеет оболочку из карбоната кальция с правильной додекаэдрической структурой около 10 микрометров в поперечнике.^[9]

Немного квазикристаллы имеют додекаэдрическую форму (см. рисунок). Некоторые обычные кристаллы, такие как гранат и алмаз также говорят, что демонстрируют "додекаэдр" привычка, но это утверждение фактически относится к ромбический додекаэдр форма.^[10]

Форма вселенной

Были предложены различные модели глобальной геометрии Вселенной. В добавок к примитивные геометрии эти предложения включают Додекаэдральное пространство Пуанкаре, положительно искривленное пространство, состоящее из правильного додекаэдра, противоположные грани которого соответствуют (с небольшим поворотом). Это было предложено Жан-Пьер Люмине и коллеги в 2003 г.,^[11][12] оптимальная ориентация модели на небе была оценена в 2008 году.^[13]

В Бертран Рассел В рассказе 1954 года «Кошмар математика: видение профессора Скверпунта» цифра 5 гласила: «Я - количество пальцев на руке. Я делаю пятиугольники и пентаграммы. И без меня додекаэдра не могло бы существовать; и, как всем известно, Вселенная - это додекаэдр. Так что, если бы не я, вселенной не могло быть ».

Заполнение пространства кубиком и билунабиротондами

Правильные додекаэдры заполняют пространство кубики и билунобиротонды (Джонсон солид 91) в соотношении 1: 1: 3.^[14][15] Только додекаэдры составляют решетку от края до края. пиритоэдры. Двунабиротунды заполняют ромбические промежутки. Каждый куб встречается с шестью билунабиротондами в трех ориентациях.

Блочная модель

Решетка додекаэдров

6 билунобиротондов вокруг куба

Связанные многогранники и мозаики

Правильный додекаэдр топологически связан с серией мозаик соотношением вершина фигуры п³.

*п32 изменения симметрии правильных мозаик: {п,3} v т е
Сферический				Евклидово	Компактная гиперболия.		Paraco.	Некомпактный гиперболический
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

Правильный додекаэдр можно преобразовать усечение последовательность в его двойной, икосаэдр:

Семейство однородных икосаэдрических многогранников
Симметрия: [5,3], (*532)							[5,3]^+, (532)
{5,3}	т {5,3}	г {5,3}	т {3,5}	{3,5}	рр {5,3}	tr {5,3}	ср {5,3}
Двойники к однородным многогранникам
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]^+ (432)	[1^+,4,3] = [3,3] (*332)		[3^+,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s2{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час2{4,3} т {3,3}	с {3,4} с {3^1,1}
		=	=	=				= или же	= или же	=
Двойники к однородным многогранникам
V4^3	V3.8^2	V (3,4)^2	V4.6^2	V3^4	V3.4^3	V4.6.8	V3^4.4	V3^3	V3.6^2	V3^5

Правильный додекаэдр является членом последовательности неоднородных многогранников и мозаик, состоящих из пятиугольников с конфигурации лица (V3.3.3.3.п). (За п > 6, последовательность состоит из мозаик гиперболической плоскости.) Эти лицо переходный цифры имеют (п32) rotational (вращательный) симметрия.

п32 мутации симметрии курносых плиток: 3.3.3.3.n
Симметрия п32	Сферический				Евклидово	Компактный гиперболический		Paracomp.
	232	332	432	532	632	732	832	∞32
Курносый цифры
Конфиг.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Гироскоп цифры
Конфиг.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Расположение вершин

Правильный додекаэдр разделяет расположение вершин с четырьмя невыпуклые равномерные многогранники и три однородные многогранники.

Пять кубики вписываются внутрь, их края являются диагоналями граней правильного додекаэдра, и вместе они составляют правильный полиэдрическое соединение из пяти кубиков. Поскольку два тетраэдра могут поместиться на чередующихся вершинах куба, пять и десять тетраэдров также могут поместиться в правильный додекаэдр.

Большой звездчатый додекаэдр	Малый дитригональный икосододекаэдр	Дитригональный додекадодекаэдр	Большой дитригональный икосододекаэдр
Соединение пяти кубиков	Соединение пяти тетраэдров	Соединение десяти тетраэдров

Звёздчатые

3 звездчатые правильного додекаэдра все правильные (невыпуклый ) многогранники: (Многогранники Кеплера – Пуансо )

	0	1	2	3
Звездчатость	Правильный додекаэдр	Малый звездчатый додекаэдр	Большой додекаэдр	Большой звездчатый додекаэдр
Диаграмма фасетов

Додекаэдрический граф

График регулярного додекаэдра
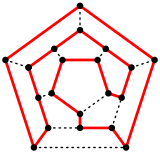А Гамильтонов цикл в додекаэдре.
Вершины	20
Края	30
Радиус	5
Диаметр	5
Обхват	5
Автоморфизмы	120 (А5 × Z2)[16]
Хроматическое число	3
Характеристики	Гамильтониан, обычный, симметричный, дистанционно-регулярный, дистанционно-переходный, 3-вершинно-связанный, планарный граф
Таблица графиков и параметров

В скелет додекаэдра (вершины и ребра) образуют график. Это один из 5 Платоновы графики, каждый - скелет своего Платоново твердое тело.

Этот граф также можно построить как обобщенный граф Петерсена грамм(10,2). Высокая степень симметрии многоугольника воспроизводится в свойствах этого графа, который дистанционно-переходный, дистанционно-регулярный, и симметричный. В группа автоморфизмов имеет порядок 120. Вершины могут быть цветной с 3 цветами, как и края, и диаметр 5.^[17]

Додекаэдрический граф Гамильтониан - есть цикл, содержащий все вершины. Действительно, это название происходит от математическая игра изобретен в 1857 г. Уильям Роуэн Гамильтон, то икозианская игра. Целью игры было найти Гамильтонов цикл по краям додекаэдра.

Ортогональная проекция

Смотрите также

• 120 ячеек, а регулярный полихорон (4-мерный многогранник, поверхность которого состоит из 120 додекаэдрических ячеек)
• Braarudosphaera bigelowii - в форме додекаэдра кокколитофора (а одноклеточный фитопланктон водоросли ).
• Додекаэдран (молекула)
• Додекаэдр пентакиса
• Курносый додекаэдр
• Усеченный додекаэдр

Рекомендации

1. Саттон, Дауд (2002), Платоновы и архимедовы тела, Wooden Books, Bloomsbury Publishing USA, стр. 55, ISBN  9780802713865.
2. Ливио, Марио (2003) [2002]. Золотое сечение: история Фи, самого удивительного числа в мире (Первая торговая книга в мягкой обложке, ред.). Нью-Йорк: Бродвей Книги. С. 70–1. ISBN  0-7679-0816-3.
3. Вайсштейн, Эрик В. «Икосаэдрическая группа». MathWorld.
4. http://mathworld.wolfram.com/images/eps-gif/DodecahedronCube_700.gif
5. http://davidf.faricy.net/polyhedra/images/dodecarect.gif
6. http://www.toshen.com/images/dodecahedronwithgoldrectang.gif
7. Флориан Каджори, История математики (1893)
8. Платон, Тимей, Перевод Джоветта [строка 1317–8]; греческое слово, переведенное как разграничение, диазографеинЖивопись в подобии жизни.
9. Хагино, К., Онума, Р., Кавачи, М. и Хоригучи, Т. (2013) «Открытие эндосимбиотической азотфиксирующей цианобактерии UCYN-A в Braarudosphaera bigelowii (Prymnesiophyceae) ". PLoS One, 8(12): e81749. Дои:10.1371 / journal.pone.0081749.
10. Додекаэдрический кристалл В архиве 12 апреля 2009 г. Wayback Machine
11. Дюме, Бель (8 октября 2003 г.). "Является ли Вселенная додекаэдром?". PhysicsWorld. Архивировано из оригинал на 2012-04-25.
12. Люмине, Жан-Пьер; Джефф Уикс; Ален Риазуэло; Роланд Лехук; Жан-Филипп Узан (09.10.2003). «Додекаэдрическая топология пространства как объяснение слабых широкоугольных температурных корреляций в космическом микроволновом фоне». Природа. 425 (6958): 593–5. arXiv:Astro-ph / 0310253. Bibcode:2003Натура.425..593л. Дои:10.1038 / природа01944. PMID  14534579. S2CID  4380713.
13. Рукема, Будевейн; Збигнев Булиньски; Агнешка Сзаневска; Николя Э. Годен (2008). «Проверка гипотезы топологии додекаэдрического пространства Пуанкаре с данными CMB WMAP». Астрономия и астрофизика. 482 (3): 747. arXiv:0801.0006. Bibcode:2008A & A ... 482..747L. Дои:10.1051/0004-6361:20078777. S2CID  1616362.
14. http://demonstrations.wolfram.com/DodecahedronAndBilunabirotunda/
15. http://www.lcv.ne.jp/~hhase/memo/m09_08b.html
16. Фрухт, Роберто (1936–1937), "Die gruppe des Petersen'schen Graphen und der Kantensysteme der Regären Polyeder", Комментарий. Математика. Helv., 9: 217–223, Дои:10.1007 / bf01258190, S2CID  121791222
17. Вайсштейн, Эрик В. «Додекаэдрический график». MathWorld.

внешняя ссылка

• Вайсштейн, Эрик В. «Правильный додекаэдр». MathWorld.
• Клитцинг, Ричард. "3D выпуклые равномерные многогранники o3o5x - лань".
• Редактируемая печатная сетка додекаэдра с интерактивным трехмерным изображением
• Равномерные многогранники
• Оригами Многогранники - Модели из модульного оригами
• Додекаэдр - 3-мерная модель, которая работает в вашем браузере
• Многогранники виртуальной реальности Энциклопедия многогранников
  • VRML #Правильный додекаэдр
• K.J.M. Маклин, Геометрический анализ пяти платоновых тел и других полурегулярных многогранников
• Додекаэдр 3D визуализация
• Стелла: многогранник-навигатор: Программное обеспечение, использованное для создания некоторых изображений на этой странице.
• Как сделать додекаэдр из пенополистирольного куба
• Греческий, индийский и китайский элементы - теория семи элементов

v т е Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	Ап	Bп	я2(п) / Dп	E6 / E7 / E8 / F4 / грамм2	ЧАСп
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукруглый	132 • 231 • 321
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	142 • 241 • 421
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукруглый
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1k2 • 2k1 • k21	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений