Усеченный октаэдр - Truncated octahedron

Усеченный октаэдр
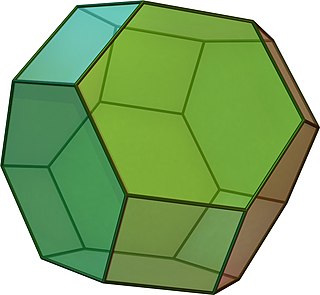(Нажмите здесь, чтобы повернуть модель)
Тип	Архимедово твердое тело Равномерный многогранник
Элементы	F = 14, E = 36, V = 24 (χ = 2)
Лица по сторонам	6{4}+8{6}
Обозначение Конвея	к bT
Символы Шлефли	т {3,4} tr {3,3} или ${\displaystyle t{\begin{Bmatrix}3\\3\end{Bmatrix}}}$
	т0,1{3,4} или т0,1,2{3,3}
Символ Wythoff	2 4 | 3 3 3 2 |
Диаграмма Кокстера
Группа симметрии	Очас, B3, [4,3], (* 432), порядок 48 Тчас, [3,3] и (* 332), порядок 24
Группа вращения	О, [4,3]^+, (432), заказ 24
Двугранный угол	4-6: arccos (-1/√3) = 125°15′51″ 6-6: arccos (-1/3) = 109°28′16″
Рекомендации	U08, C20, W7
Характеристики	Полурегулярный выпуклый параллелоэдр пермутоэдр
Цветные лица	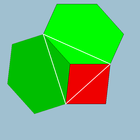4.6.6 (Фигура вершины )
Шестигранник Тетракис (двойственный многогранник )	Сеть

3D модель усеченного октаэдра

В геометрия, то усеченный октаэдр является Архимедово твердое тело. Имеет 14 граней (8 обычных шестиугольник и 6 квадрат ), 36 ребер и 24 вершины. Поскольку каждая его грань имеет точечная симметрия усеченный октаэдр - это зоноэдр. Это также Многогранник Гольдберга грамм_IV(1,1), содержащие квадратные и шестиугольные грани. Как и куб, он может разбивать (или «упаковывать») трехмерное пространство в виде пермутоэдр.

Усеченный октаэдр Бакминстер Фуллер назвал «меконом».^[1]

Его двойственный многогранник это тетракис шестигранник.

Если исходный усеченный октаэдр имеет единичную длину ребра, его двойственный куб тетракиса имеет длину кромки 9/8√2 и 3/2√2.

Строительство

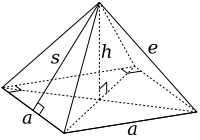Усеченный октаэдр строится из правильного октаэдр с длиной стороны 3а удалением шести правых квадратные пирамиды, по одному с каждой точки. Эти пирамиды имеют длину обеих сторон основания (а) и длина боковой стороны (е) из а, чтобы сформировать равносторонние треугольники. Тогда базовая площадь а². Обратите внимание, что эта форма в точности похожа на половину октаэдра или Джонсон солид J₁.

Из свойств квадратных пирамид теперь мы можем найти наклонную высоту, s, а высота, часпирамиды:

${\displaystyle {\begin{aligned}h&={\sqrt {e^{2}-{\tfrac {1}{2}}a^{2}}}&&={\tfrac {1}{\sqrt {2}}}a\\s&={\sqrt {h^{2}+{\tfrac {1}{4}}a^{2}}}&&={\sqrt {{\tfrac {1}{2}}a^{2}+{\tfrac {1}{4}}a^{2}}}&&={\tfrac {\sqrt {3}}{2}}a\end{aligned}}}$

Громкость, Vпирамиды определяется выражением:

${\displaystyle V={\tfrac {1}{3}}a^{2}h={\tfrac {\sqrt {2}}{6}}a^{3}}$

Поскольку шесть пирамид удаляются усечением, общий потерянный объем составляет √2а³.

Ортогональные проекции

В усеченный октаэдр имеет пять специальных ортогональные проекции, с центром, на вершине, на двух типах ребер и двух типах граней: шестиугольник и квадрат. Последние два соответствуют букве B₂ и А₂ Самолеты Кокстера.

Ортогональные проекции

В центре	Вершина	Край 4-6	Край 6-6	Лицо Квадрат	Лицо Шестиугольник
Твердый
Каркас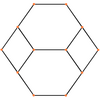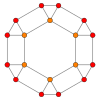
Двойной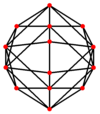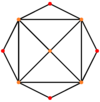
Проективный симметрия	[2]	[2]	[2]	[4]	[6]

Сферическая черепица

Усеченный октаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.

	квадрат -центрированный	шестиугольник -центрированный
Ортографическая проекция	Стереографические проекции

Координаты

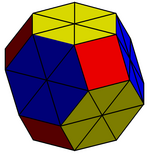Ортогональная проекция в Ограничительная рамка (±2,±2,±2)	Усеченный октаэдр, в котором шестиугольники заменены на 6 копланарных треугольников. Есть 8 новых вершин в: (± 1, ± 1, ± 1).	Усеченный октаэдр подразделяется на топологические ромбический триаконтаэдр

Все перестановки из (0, ± 1, ± 2) являются Декартовы координаты из вершины из усеченный октаэдр с длиной ребра a = √ 2 с центром в начале координат. Таким образом, вершины также являются углами 12 прямоугольников, длинные края которых параллельны осям координат.

В рёберные векторы иметь декартовы координаты (0, ±1, ±1) и их перестановки. Нормали граней (нормализованные перекрестные произведения ребер с общей вершиной) шести квадратных граней равны (0, 0, ±1), (0, ±1, 0) и (±1, 0, 0). Нормали восьми шестиугольных граней равны (±1/√3, ±1/√3, ±1/√3). Скалярное произведение между парами двух нормалей граней - это косинус двугранного угла между соседними гранями, либо -1/3 или -1/√3. Двугранный угол составляет приблизительно 1,9 · 10 633 радиана (109,471 ° OEIS: A156546) на краях, разделяемых двумя шестиугольниками, или 2,186276 радиан (125,263 ° OEIS: A195698) на ребрах, общих для шестиугольника и квадрата.

Рассечение

Усеченный октаэдр можно разрезать на центральный октаэдр, в окружении 8 треугольный купол на каждой грани и 6 квадратные пирамиды над вершинами.^[2]

Удаление центрального октаэдра и 2 или 4 треугольных куполов создает два Тороиды Стюарта, с двугранной и тетраэдрической симметрией:

Род 2	Род 3
D3D, [2^+, 6], (2 * 3), порядок 12	Тd, [3,3], (* 332), порядок 24

Пермутоэдр

Усеченный октаэдр также может быть представлен еще более симметричными координатами в четырех измерениях: все перестановки (1, 2, 3, 4) образуют вершины усеченного октаэдра в трехмерном подпространстве Икс + у + z + ш = 10. Следовательно, усеченный октаэдр - это пермутоэдр порядка 4: каждая вершина соответствует перестановке (1, 2, 3, 4), и каждое ребро представляет собой одну попарную замену двух элементов.

Площадь и объем

Площадь А и объем V усеченного октаэдра реберной длины а находятся:

${\displaystyle {\begin{aligned}A&=\left(6+12{\sqrt {3}}\right)a^{2}&&\approx 26.784\,6097a^{2}\\V&=8{\sqrt {2}}a^{3}&&\approx 11.313\,7085a^{3}.\end{aligned}}}$

Равномерная окраска

Есть два равномерные раскраски, с тетраэдрическая симметрия и октаэдрическая симметрия, и две 2-однородные раскраски с двугранная симметрия как усеченная треугольная антипризма. Каждому дано конструктивное название. Их Обозначения многогранника Конвея дан в скобках.

1-униформа		2-униформа
Очас, [4,3], (*432) Заказ 48	Тd, [3,3], (*332) Заказ 24	D4ч, [4,2], (*422) Заказ 16	D3D, [2^+,6], (2*3) Заказ 12
122 раскраски	123 раскраски	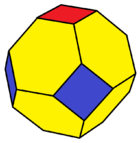122 и 322 раскраски	122 и 123 раскраски
Усеченный октаэдр (к)	Скошенный тетраэдр (бТ)	Усеченная квадратная бипирамида (tdP4)	Усеченная треугольная антипризма (tA3)

Химия

В усеченный октаэдр существует в структуре фожазит кристаллы.

Скрытие данных

В усеченный октаэдр (фактически, обобщенный усеченный октаэдр) появляется в анализе ошибок модуляции индекса квантования (QIM) в сочетании с кодированием с повторением.^[3]

Связанные многогранники

Усеченный октаэдр - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]^+ (432)	[1^+,4,3] = [3,3] (*332)		[3^+,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s2{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час2{4,3} т {3,3}	с {3,4} с {3^1,1}
		=	=	=				= или же	= или же	=
Двойники к однородным многогранникам
V4^3	V3.8^2	V (3,4)^2	V4.6^2	V3^4	V3.4^3	V4.6.8	V3^4.4	V3^3	V3.6^2	V3^5

Он также существует как полное усечение семейства тетраэдров:

Семейство равномерных тетраэдрических многогранников
Симметрия: [3,3], (*332)							[3,3]^+, (332)
{3,3}	т {3,3}	г {3,3}	т {3,3}	{3,3}	рр {3,3}	tr {3,3}	ср {3,3}
Двойники к однородным многогранникам
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Мутации симметрии

*п32 мутации симметрии полностью усеченных мозаик: 4.6.2n [ v т е ]
Сим. *п32 [п,3]	Сферический				Евклид.	Компактная гиперболия.		Paraco.	Некомпактный гиперболический
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]	[3i, 3]
Цифры
Конфиг.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Конфиг.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

*nn2 мутации симметрии полностью усеченных мозаик: 4.2п.2п [ v т е ]
Симметрия *nn2 [п, п]	Сферический		Евклидово	Компактный гиперболический				Paracomp.
	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Фигура
Конфиг.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Двойной
Конфиг.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Этот многогранник входит в последовательность однородных узоров с вершиной фигуры (4.6.2п) и Диаграмма Кокстера – Дынкина . За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры ), показанные ниже в виде сферических мозаик. За п > 6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.

Усеченный октаэдр топологически связан как часть последовательности однородных многогранников и мозаик с фигуры вершин п.6.6, продолжающийся в гиперболической плоскости:

*п32 мутации симметрии усеченных мозаик: п.6.6 [ v т е ]
Сим. *п42 [n, 3]	Сферический				Евклид.	Компактный		Parac.	Некомпактный гиперболический
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
Усеченный цифры
Конфиг.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
н-кис цифры
Конфиг.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Усеченный октаэдр топологически связан как часть последовательности однородных многогранников и мозаик с фигуры вершин 4.2п.2п, простирающаяся в гиперболическую плоскость:

*п42 мутации симметрии усеченных мозаик: 4,2п.2п [ v т е ]
Симметрия *п42 [n, 4]	Сферический		Евклидово	Компактный гиперболический				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Усеченный цифры
Конфиг.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
н-кис цифры
Конфиг.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Связанные многогранники

В усеченный октаэдр (усеченный битами куб), является первым в последовательности усеченных битов гиперкубы:

Битрорезанные гиперкубы

Изображение							...
Имя	Битусеченный куб	Обрезанный тессеракт	Обрезанный бит 5-куб	Bitruncated 6-куб	Bitruncated 7-cube	Обрезанный битами 8-куб
Coxeter
Фигура вершины	() v {}	{} v {}	{} v {3}	{} v {3,3}	{} v {3,3,3}	{} v {3,3,3,3}

Мозаики

Усеченный октаэдр существует в трех разных формах. выпуклые однородные соты (заполняющие пространство мозаики ):

Усеченный кубический	Усеченный кубический	Усеченная чередующаяся кубическая

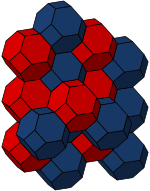В клеточно-транзитивный усеченные кубические соты также можно рассматривать как Мозаика Вороного из объемно-центрированная кубическая решетка. Усеченный октаэдр - один из пяти трехмерных первичных элементов. параллелоэдры.

Объекты

Детская игровая площадка сети часто включают усеченные октаэдры.

• 

  древние китайские кости

• 

  скульптура в Бонн

• 

  Кубик Рубика вариант

• 

  модель сделана из Полидрона конструктор

• 

  Пирит кристалл

Усеченный октаэдрический граф

Усеченный октаэдрический граф
3-х кратно симметричный Диаграмма Шлегеля
Вершины	24
Края	36
Автоморфизмы	48
Хроматическое число	2
Толщина книги	3
Номер очереди	2
Характеристики	Кубический, Гамильтониан, обычный, нулевой симметричный
Таблица графиков и параметров

в математический поле теория графов, а усеченный октаэдрический граф это граф вершин и ребер усеченного октаэдра, один из Архимедовы тела. Имеет 24 вершины и 36 ребер, и является кубический Архимедов граф.^[4] Она имеет толщина книги 3 и номер очереди 2.^[5]

Как Гамильтониан кубический граф, его можно представить как Обозначение LCF несколькими способами: [3, −7, 7, −3]⁶, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7]²и [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9 , 9, 7, −5, −7, 3].^[6]

Три разных гамильтоновых цикла, описываемые тремя разными Обозначения LCF для усеченного октаэдрического графа

Рекомендации

1. «Усеченный октаэдр». Вольфрам Mathworld.
2. Доски, Алекс. "Приключения среди тороидов - Глава 5 - Простейшие (R) (A) (Q) (T) Тороиды рода p = 1". www.doskey.com.
3. Perez-Gonzalez, F .; Balado, F .; Мартин, J.R.H. (2003). «Анализ производительности существующих и новых методов сокрытия данных с информацией об известных хостах в дополнительных каналах». Транзакции IEEE при обработке сигналов. 51 (4): 960–980. Дои:10.1109 / TSP.2003.809368.
4. Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269
5. Вольц, Джессика; Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
6. Вайсштейн, Эрик В. «Усеченный октаэдрический граф». MathWorld.

• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN  0-486-23729-X. (Раздел 3–9)
• Фрейтас, Роберт А. мл. «Равномерное заполнение пространства только усеченными октаэдрами». Рисунок 5.5 из Наномедицина, Том I: Основные возможности, Landes Bioscience, Джорджтаун, Техас, 1999 г.. Получено 2006-09-08. Внешняя ссылка в | publisher = (помощь)
• Гайха, П., Гуха, С.К. (1977). «Смежные вершины пермутоэдра». Журнал SIAM по прикладной математике. 32 (2): 323–327. Дои:10.1137/0132025.
• Харт, Джордж У. «VRML-модель усеченного октаэдра». Виртуальные многогранники: энциклопедия многогранников. Получено 2006-09-08. Внешняя ссылка в | publisher = (помощь)
• Мэдер, Роман. «Однородные многогранники: усеченный октаэдр». Получено 2006-09-08.
• Александров, А.Д. (1958). Konvexe Polyeder. Берлин: Springer. п. 539. ISBN  3-540-23158-7.
• Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN  0-521-55432-2.

внешняя ссылка

• Эрик В. Вайсштейн, Усеченный октаэдр (Архимедово твердое тело ) в MathWorld.
  • Вайсштейн, Эрик В. «Усеченный октаэдрический граф». MathWorld.
• Вайсштейн, Эрик В. «Пермутоэдр». MathWorld.
• Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3x4o - носок".
• Редактируемая печатная сетка усеченного октаэдра с интерактивным трехмерным изображением