Призматоид - Prismatoid

Призматоид с параллельными гранями A₁ и A₃, срединным поперечным сечением A₂ и высотой h

В геометрия, а призматоид это многогранник чей вершины все лежат в двух параллельных плоскостях. Его боковые грани могут быть трапециевидными или треугольными.^[1] Если обе плоскости имеют одинаковое количество вершин, а боковые грани либо параллелограммы или же трапеции, это называется призмоидный.^[2]

Объем

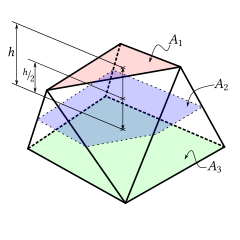
Если площади двух параллельных граней равны A₁ и А₃, площадь поперечного сечения пересечения призматоида с плоскостью посередине между двумя параллельными гранями равна A₂, а высота (расстояние между двумя параллельными гранями) равна h, тогда объем призматоида определяется выражением ${\displaystyle V={\frac {h(A_{1}+4A_{2}+A_{3})}{6}}}$^[3] или же ${\displaystyle V={\frac {nh(a^{2}+4b^{2}+c^{2})}{24\tan(180/n)}}}$(Из этой формулы сразу следует интеграция площадь, параллельную двум плоскостям вершин, на Правило Симпсона, поскольку это правило точно для интегрирования многочлены степени до 3, и в этом случае площадь не более квадратичная функция в высоту.)

Призматоидные семейства

Пирамиды	Клинья	Параллелепипеды	Призмы	Антипризмы			Купола	Фруста

Семейства призматоидов включают:

• Пирамиды, в которой одна плоскость содержит только одну точку;
• Клинья, в которой одна плоскость содержит только две точки;
• Призмы, многоугольники которого в каждой плоскости совпадают и соединены прямоугольниками или параллелограммами;
• Антипризмы, многоугольники которого в каждой плоскости совпадают и соединены чередующейся полосой треугольников;
• Звездные антипризмы;
• Купола, в котором многоугольник в одной плоскости содержит вдвое больше точек, чем другой, и соединен с ним чередующимися треугольниками и прямоугольниками;
• Фруста получено усечение пирамиды;
• Четырехугольник с лицом шестигранный призматоиды:
  1. Параллелепипеды - шесть параллелограмм лица
  2. Ромбоэдры - шесть ромб лица
  3. Тригональные трапецоэдры - шесть конгруэнтных граней ромба
  4. Кубоиды - шесть прямоугольных граней
  5. Четырехугольник усеченный - ан вершина -усеченный квадратная пирамида
  6. Куб - шесть квадратных граней

Высшие измерения

В целом многогранник призматоидален, если его вершины существуют в двух гиперплоскости. Например, в четырех измерениях два многогранника могут быть размещены в двух параллельных трехмерных пространствах и соединены многогранными сторонами.

Четырехгранно-кубооктаэдрический купол.

Рекомендации

1. Уильям Ф. Керн, Джеймс Р. Бланд, Твердое измерение с доказательствами, 1938, с.75
2. Клауди Альсина, Роджер Б. Нельсен: Математическая космическая одиссея: сплошная геометрия в 21 веке. Математическая ассоциация Америки, 2015 г., ISBN  9780883853580, стр. 85-89
3. Б. Э. Месерв, Р. Э. Пингри: Некоторые примечания к формуле призмоидальной оболочки. Учитель математики, Vol. 45, No. 4 (апрель 1952 г.), стр. 257-263

внешняя ссылка

• Вайсштейн, Эрик В. «Призматоид». MathWorld.