Bifrustum - Bifrustum

Набор бифруста
Пример шестиугольного двукрылка
Лица	2 n-угольники, 2н трапеции
Края	5н
Вершины	3n
Группа симметрии	Dнэ, [n, 2], (* n22)
Двойной многогранник	Удлиненные бипирамиды
Характеристики	выпуклый

An п-агональный двустворчатый это многогранник состоит из трех параллельных плоскостей п-агоны, причем средняя плоскость самая большая, а верхняя и нижняя обычно совпадают.

Его можно построить как два конгруэнтных фруста совмещены в плоскости симметрии, а также как бипирамида с усечением двух полярных вершин.

Они есть двойники семье удлиненные бипирамиды.

Формы

Три бифрустума двойники до трех Твердые тела Джонсона, J14-16. В целом n-агональный двустворчатый имеет 2n трапеций, 2 n-агона и двойственен удлиненные дипирамиды.

Двустворчатый треугольный	Двустворчатый квадратный	Пятиугольный двустворчатый
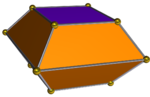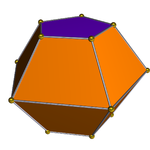6 трапеций, 2 треугольника. Двойной к удлиненная треугольная бипирамида, J14	8 трапеций, 2 квадрата. Двойной к удлиненная квадратная бипирамида, J15	10 трапеций, 2 пятиугольника. Двойной к удлиненная пятиугольная бипирамида, J16