Октаэдр - Octahedron

Правильный октаэдр
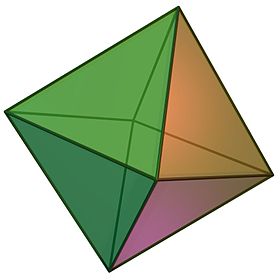(Нажмите здесь, чтобы повернуть модель)
Тип	Платоново твердое тело
Элементы	F = 8, E = 12 V = 6 (χ = 2)
Лица по сторонам	8{3}
Обозначение Конвея	О в
Символы Шлефли	{3,4}
Символы Шлефли	г {3,3} или ${displaystyle {egin {Bmatrix} 3 3end {Bmatrix}}}$
Конфигурация лица	V4.4.4
Символ Wythoff	4 \| 2 3
Диаграмма Кокстера
Симметрия	О_час, ДО Н.Э₃, [4,3], (*432)
Группа вращения	О, [4,3]⁺, (432)
Рекомендации	U₀₅, C₁₇, W₂
Характеристики	обычный, выпуклый дельтаэдр
Двугранный угол	109,47122 ° = arccos (-¹⁄₃)
3.3.3.3 (Фигура вершины )	Куб (двойственный многогранник )
Сеть

3D-модель правильного октаэдра.

В геометрия, октаэдр (множественное число: октаэдры) - это многогранник с восемью гранями, двенадцатью ребрами и шестью вершинами. Этот термин чаще всего используется для обозначения обычный октаэдр, а Платоново твердое тело состоит из восьми равносторонние треугольники, четыре из которых встречаются на каждом вершина.

Правильный октаэдр - это двойственный многогранник из куб. Это исправленный тетраэдр. Это квадрат бипирамида в любом из трех ортогональный ориентации. Это тоже треугольник антипризма в любой из четырех ориентаций.

Октаэдр - это трехмерный случай более общей концепции кросс-многогранник.

Правильный октаэдр - это 3 мяча в Манхэттен ( $ℓ$ ₁) метрика.

Правильный октаэдр

Размеры

Если длина ребра правильного октаэдра равна а, то радиус ограниченного сфера (тот, который касается октаэдра во всех вершинах)

{displaystyle r_ {u} = {frac {sqrt {2}} {2}} около 0,707cdot a}

и радиус вписанной сферы (касательная к каждой из граней октаэдра)

{displaystyle r_ {i} = {frac {sqrt {6}} {6}} около 0,408cdot a}

в то время как средний радиус, который касается середины каждого края, равен

{displaystyle r_ {m} = {frac {1} {2}} a = 0,5cdot a}

Ортогональные проекции

В октаэдр имеет четыре специальных ортогональные проекции, по центру, на ребре, вершине, грани и по нормали к грани. Второй и третий соответствуют букве B₂ и А₂ Самолеты Кокстера.

Ортогональные проекции
В центре	Край	Лицо Нормальный	Вершина	Лицо
Изображение
Проективный симметрия	[2]	[2]	[4]	[6]

Сферическая черепица

Октаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.

Ортографическая проекция	Стереографическая проекция

Декартовы координаты

Октаэдр с длиной ребра √2 может быть размещен с центром в начале координат и вершинами на осях координат; то Декартовы координаты вершин тогда

( ±1, 0, 0 );

( 0, ±1, 0 );

( 0, 0, ±1 ).

В Икс–у–z Декартова система координат, октаэдр с центром координаты (а, б, c) и радиус р - множество всех точек (Икс, у, z) такие, что

{displaystyle left | x-aight | + left | y-bight | + left | z-cight | = r.}

Площадь и объем

Площадь поверхности А и объем V правильного октаэдра реберной длины а находятся:

{displaystyle A = 2 {sqrt {3}} a ^ {2} приблизительно 3,464a ^ {2}}

{displaystyle V = {frac {1} {3}} {sqrt {2}} a ^ {3} примерно 0,471a ^ {3}}

Таким образом, объем в четыре раза больше, чем у обычного тетраэдр с одинаковой длиной ребра, а площадь поверхности в два раза (потому что у нас 8, а не 4 треугольника).

Если октаэдр был растянут так, что он подчиняется уравнению

{displaystyle left | {frac {x} {x_ {m}}} ight | + left | {frac {y} {y_ {m}}} ight | + left | {frac {z} {z_ {m}}} ight | = 1,}

формулы для площади поверхности и объема расширяются, чтобы стать

{displaystyle A = 4, x_ {m}, y_ {m}, z_ {m} imes {sqrt {{frac {1} {x_ {m} ^ {2}}} + {frac {1} {y_ {m}) } ^ {2}}} + {frac {1} {z_ {m} ^ {2}}}}},}

{displaystyle V = {frac {4} {3}}, x_ {m}, y_ {m}, z_ {m}.}

Кроме того, тензор инерции вытянутого октаэдра равен

{displaystyle I = {egin {bmatrix} {frac {1} {10}} m (y_ {m} ^ {2} + z_ {m} ^ {2}) & 0 & 0 0 & {frac {1} {10}} m (x_ {m} ^ {2} + z_ {m} ^ {2}) & 0 0 & 0 & {frac {1} {10}} m (x_ {m} ^ {2} -y_ {m} ^ {2 }) end {bmatrix}}.}

Они сводятся к уравнениям для правильного октаэдра, когда

{displaystyle x_ {m} = y_ {m} = z_ {m} = a, {frac {sqrt {2}} {2}}.}

Геометрические отношения

Октаэдр представляет собой центральное пересечение двух тетраэдров.

Интерьер сложный двух двойных тетраэдры октаэдр, и это соединение, называемое Stella Octangula, это его первая и единственная звездчатость. Соответственно, правильный октаэдр - это результат отсечения от правильного тетраэдра четырех правильных тетраэдров половинного линейного размера (т.е. исправление тетраэдр). Вершины октаэдра лежат в средних точках ребер тетраэдра, и в этом смысле он относится к тетраэдру так же, как кубооктаэдр и икосододекаэдр относятся к другим Платоновым телам. Также можно разделить ребра октаэдра в соотношении Золотая середина определить вершины икосаэдр. Это делается путем размещения векторов по краям октаэдра таким образом, чтобы каждая грань была ограничена циклом, а затем аналогичным образом разбивая каждое ребро на золотую середину в направлении его вектора. Есть пять октаэдров, которые определяют любой данный икосаэдр таким образом, и вместе они определяют регулярное соединение.

Октаэдры и тетраэдры можно чередовать, чтобы сформировать однородные по вершине, ребру и граням мозаика пространства, называется октет фермы к Бакминстер Фуллер. Это единственная такая мозаика, за исключением обычной мозаики кубики, и является одним из 28 выпуклые однородные соты. Другой - мозаика октаэдров и кубооктаэдр.

Октаэдр уникален среди Платоновых тел тем, что в каждой вершине встречается четное число граней. Следовательно, это единственный член этой группы, у которого есть зеркальные плоскости, которые не проходят ни через одну из граней.

Используя стандартную номенклатуру для Твердые тела Джонсона, октаэдр назовем квадратная бипирамида. Усечение двух противоположных вершин приводит к квадратный двустворчатый.

Октаэдр 4-связный, что означает, что нужно удалить четыре вершины, чтобы разъединить оставшиеся вершины. Это один из четырех 4-х соединенных симплициальный хорошо покрытый многогранники, что означает, что все максимальные независимые множества его вершин имеют одинаковый размер. Остальные три многогранника с этим свойством являются пятиугольная дипирамида, то курносый дисфеноид, и неправильный многогранник с 12 вершинами и 20 треугольными гранями.^[1]

Октаэдр также может быть сгенерирован как трехмерный суперэллипсоид со всеми значениями, установленными на 1.

Равномерная окраска и симметрия

Есть 3 равномерные раскраски октаэдра, названного цветами треугольных граней, окружающих каждую вершину: 1212, 1112, 1111.

Октаэдр группа симметрии это O_час, порядка 48, трехмерное гипероктаэдрическая группа. Эта группа подгруппы включить D_3D (порядок 12) группа симметрии треугольного антипризма; D_4ч (порядок 16) группа симметрии квадрата бипирамида; и т_d (порядок 24) группа симметрии выпрямленный тетраэдр. Эти симметрии можно подчеркнуть разной окраской лиц.

Имя	Октаэдр	Исправленный тетраэдр (Тетратетраэдр)	Треугольный антипризма	Квадрат бипирамида	Ромбический фузил
Изображение (Раскраска лица)	(1111)	(1212)	(1112)	(1111)	(1111)
Диаграмма Кокстера		=
Символ Шлефли	{3,4}	г {3,3}	с {2,6} ср {2,3}	фут {2,4} { } + {4}	ftr {2,2} { } + { } + { }
Символ Wythoff	4 \| 3 2	2 \| 4 3	2 \| 6 2 \| 2 3 2
Симметрия	О_час, [4,3], (*432)	Т_d, [3,3], (*332)	D_3D, [2⁺,6], (2*3) D₃, [2,3]⁺, (322)	D_4ч, [2,4], (*422)	D_2ч, [2,2], (*222)
Заказ	48	24	12 6	16	8

Сети

Он имеет одиннадцать аранжировок сети.

Двойной

Октаэдр - это двойственный многогранник к куб.

Если длина ребра октаэдра ${displaystyle = a}$ , то длина ребра двойственного куба ${displaystyle = {sqrt {2}} a}$ .

Огранка

Униформа тетрагемигексаэдр это тетраэдрическая симметрия огранка правильного октаэдра, разделяющего край и расположение вершин. У него четыре треугольных грани и три центральных квадрата.

Октаэдр	Тетрагемигексаэдр

Неправильные октаэдры

Следующие многогранники комбинаторно эквивалентны правильному многограннику. Все они имеют шесть вершин, восемь треугольных граней и двенадцать ребер, которые однозначно соответствуют характеристикам правильного октаэдра.

Треугольный антипризмы: Две грани равносторонние, лежат на параллельных плоскостях и имеют общую ось симметрии. Остальные шесть треугольников равнобедренные.
Тетрагональный бипирамиды, в котором хотя бы один из экваториальных четырехугольников лежит на плоскости. Правильный октаэдр - это частный случай, когда все три четырехугольника представляют собой плоские квадраты.
Многогранник Шёнхардта, невыпуклый многогранник, который нельзя разбить на тетраэдры без введения новых вершин.
Октаэдр Брикара, невыпуклый самопересечение гибкий многогранник

Другие выпуклые октаэдры

В более общем смысле, октаэдром может быть любой многогранник с восемью гранями. Правильный октаэдр имеет 6 вершин и 12 ребер, минимум для октаэдра; неправильные октаэдры могут иметь до 12 вершин и 18 ребер.^[2]Есть 257 топологически различных выпуклый октаэдры, исключая зеркальные изображения. Более конкретно, существует 2, 11, 42, 74, 76, 38, 14 для октаэдров с 6–12 вершинами соответственно.^[3]^[4] (Два многогранника являются «топологически разными», если они имеют внутренне различное расположение граней и вершин, так что невозможно преобразовать один в другой, просто изменяя длину ребер или углы между ребрами или гранями.)

Некоторые более известные неправильные октаэдры включают следующее:

Гексагональная призма: Две грани параллельны правильным шестиугольникам; шесть квадратов связывают соответствующие пары граней шестиугольника.
Семиугольный пирамида: Одно лицо - семиугольник (обычно правильный), а остальные семь граней - треугольники (обычно равнобедренные). Не все треугольные грани могут быть равносторонними.
Усеченный тетраэдр: Четыре грани тетраэдра усечены, чтобы стать правильными шестиугольниками, и есть еще четыре грани равностороннего треугольника, где каждая вершина тетраэдра была усечена.
Тетрагональный трапецоэдр: Восемь граней совпадают воздушные змеи.

Октаэдра в физическом мире

Октаэдра в природе

Флюорит октаэдр.

Природные кристаллы алмаз, квасцы или же флюорит обычно октаэдрические, так как заполняющие пространство четырехгранно-октаэдрические соты.
Плиты камасит сплав в октаэдрит метеориты расположены параллельно восьми граням октаэдра.
Многие ионы металлов координировать шесть лигандов в октаэдрической или искаженный октаэдрическая конфигурация.
Узоры Widmanstätten в никель -утюг кристаллы

Октаэдры в искусстве и культуре

Два идентично сформированных змеи рубика может аппроксимировать октаэдр.

Особенно в ролевые игры, это твердое тело известно как "d8", одно из наиболее распространенных многогранная игральная кость.
Если каждое ребро октаэдра заменить на одно-ом резистор, сопротивление между противоположными вершинами равно 1/2 ом, а между соседними вершинами 5/12 ом.^[5]
Шесть музыкальных нот могут быть расположены на вершинах октаэдра таким образом, что каждое ребро представляет диаду согласных, а каждая грань представляет собой триаду согласных; видеть гексани.

Тетраэдрическая ферма

Каркас из повторяющихся тетраэдров и октаэдров был изобретен Бакминстер Фуллер в 1950-х годах, известный как космический каркас, обычно считается самой сильной структурой для сопротивления консоль стрессы.

Связанные многогранники

Правильный октаэдр можно дополнить до тетраэдр добавлением 4 тетраэдров на чередующихся гранях. Добавление тетраэдров ко всем 8 граням создает звездчатый октаэдр.

тетраэдр	звездчатый октаэдр

Октаэдр - один из семейства однородных многогранников, связанных с кубом.

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s₂{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час₂{4,3} т {3,3}	с {3,4} с {3^1,1}

		=	=	=				= или же	= или же	=

Двойники к однородным многогранникам
V4³	V3.8²	V (3,4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Это также один из простейших примеров гиперсимплекс, многогранник, образованный некоторыми пересечениями гиперкуб с гиперплоскость.

Октаэдр топологически связан как часть последовательности правильных многогранников с Символы Шлефли {3,п}, переходя в гиперболическая плоскость.

*п32 изменения симметрии правильных мозаик: {3,п} [ v т е ]
Сферический				Евклид.	Компактный гипер.		Paraco.	Некомпактный гиперболический

3.3	3³	3⁴	3⁵	3⁶	3⁷	3⁸	3^∞	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

Тетратетраэдр

Правильный октаэдр тоже можно считать исправленный тетраэдр - и может быть назван тетратраэдр. Это можно показать на двухцветной модели лица. При такой раскраске октаэдр имеет тетраэдрическая симметрия.

Сравните эту последовательность усечения между тетраэдром и его двойником:

Семейство равномерных тетраэдрических многогранников
Симметрия: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	т {3,3}	г {3,3}	т {3,3}	{3,3}	рр {3,3}	tr {3,3}	ср {3,3}
Двойники к однородным многогранникам

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Вышеупомянутые формы также могут быть реализованы как срезы, ортогональные длинной диагонали тессеракт. Если эта диагональ ориентирована вертикально с высотой 1, то первые пять слоев выше расположены на высоте р, 3/8, 1/2, 5/8, и s, куда р любое число в диапазоне 0 < р ≤ 1/4, и s любое число в диапазоне 3/4 ≤ s < 1.

Октаэдр как тетратраэдр существует в последовательности симметрий квазирегулярных многогранников и мозаик с конфигурации вершин (3.п)², переходя от мозаики сферы к евклидовой плоскости и к гиперболической плоскости. С орбифолдная запись симметрия *п32 все эти мозаики Конструкции Wythoff в пределах фундаментальная область симметрии, с образующими точками в правом углу области.^[6]^[7]

*п32 орбифолдные симметрии квазирегулярных мозаик: (3.п)²
Строительство	Сферический			Евклидово	Гиперболический
Строительство	*332	*432	*532	*632	*732	*832...	*∞32
Квазирегулярный цифры
Вершина	(3.3)²	(3.4)²	(3.5)²	(3.6)²	(3.7)²	(3.8)²	(3.∞)²

Тригональная антипризма

Как тригональная антипризма октаэдр относится к семейству гексагональной диэдральной симметрии.

Однородные шестиугольные двугранные сферические многогранники
Симметрия: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	т {6,2}	г {6,2}	т {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	с {2,6}
Двойники к униформе

V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Семья униформы п-гональный антипризмы [ v т е ]
Изображение многогранника												...	Апейрогональная антипризма
Сферическое мозаичное изображение												Плоское мозаичное изображение
Конфигурация вершины п.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Квадратная бипирамида

«Обычное» правое (симметричное) п-гональный бипирамиды:
Имя	Дигональная бипирамида	Треугольная бипирамида (J₁₂)	Квадратная бипирамида (O)	Пятиугольная бипирамида (J₁₃)	Гексагональная бипирамида	Гептагональная бипирамида	Восьмиугольная бипирамида	Эннеагональная бипирамида	Десятиугольная бипирамида	...	Апейрогональная бипирамида
Многогранник изображение										...
Сферическая черепица изображение										Плоская черепица изображение
Конфигурация лица	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Диаграмма Кокстера										...

Смотрите также

внешняя ссылка

"Октаэдр". Британская энциклопедия. 19 (11-е изд.). 1911 г.
Вайсштейн, Эрик В. "Октаэдр". MathWorld.
Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3o4o - oct".
Редактируемая печатная сетка октаэдра с интерактивным трехмерным изображением
Бумажная модель октаэдра
K.J.M. Маклин, Геометрический анализ пяти платоновых тел и других полурегулярных многогранников
Равномерные многогранники
Многогранники виртуальной реальности Энциклопедия многогранников
- Обозначение Конвея для многогранников Попробуйте: dP4

Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / грамм₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукуб	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] Финбоу, Артур С .; Hartnell, Bert L .; Новаковски, Ричард Дж .; Пламмер, Майкл Д. (2010). «На хорошо покрытых триангуляциях. III». Дискретная прикладная математика. 158 (8): 894–912. Дои:10.1016 / j.dam.2009.08.002. МИСТЕР 2602814.

[2] «Архивная копия». Архивировано из оригинал 10 октября 2011 г.. Получено 2 мая 2006.CS1 maint: заархивированная копия как заголовок (связь)

[3] Подсчет многогранников

[4] «Архивная копия». Архивировано из оригинал 17 ноября 2014 г.. Получено 14 августа 2016.CS1 maint: заархивированная копия как заголовок (связь)

[5] Кляйн, Дуглас Дж. (2002). «Правила суммы сопротивления и дистанции» (PDF). Croatica Chemica Acta. 75 (2): 633–649. Архивировано из оригинал (PDF) 10 июня 2007 г.. Получено 30 сентября 2006.

[6] Coxeter Правильные многогранники, Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (Глава V: Калейдоскоп, Раздел: 5.7 Конструкция Витхоффа)

[7] Двумерные мутации симметрии Дэниел Хьюсон

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Многогранники
По количеству лиц
1–10 лиц	Моноэдр Дигедрон Трехгранник Тетраэдр Пентаэдр Шестигранник Гептаэдр Октаэдр Эннеэдр Декаэдр
11–20 лиц	Гендекаэдр Додекаэдр Тридекаэдр Тетрадекаэдр Пентадекаэдр Гексадекаэдр Гептадекаэдр Октадекаэдр Эннеадекаэдр Икосаэдр
> 21 лицо	Икоситетраэдр (24) Триаконтаэдр (30) Икосододекаэдр (32) Гексеконтаэдр (60) Эннаконтаэдр (90) Гектотриадиоэдр (132) Апейроэдр (∞)

Твердые тела Джонсона
Пирамиды, купола и ротонды	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Изменено пирамиды	удлиненная треугольная пирамида удлиненная квадратная пирамида удлиненная пятиугольная пирамида гировидная квадратная пирамида гировидная пятиугольная пирамида треугольная бипирамида квадратная бипирамида пятиугольная бипирамида удлиненная треугольная бипирамида удлиненная квадратная бипирамида удлиненная пятиугольная бипирамида гиродлинная квадратная бипирамида
Изменено купола и ротонды	удлиненный треугольный купол удлиненный квадратный купол удлиненный пятиугольный купол удлиненная пятиугольная ротонда гировидный треугольный купол гировидный квадратный купол гиродлинная пятиугольная куполка гировидная пятиугольная ротонда гиробифастигий треугольная ортобикупола квадратный ортобикупола квадратная гиробикупола пятиугольная ортобикупола пятиугольная гиробикупола пятиугольная орто-куполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда ортобикупола удлиненно-треугольной формы удлиненно-треугольная гиробикупола удлиненная квадратная гиробикупола удлиненные пятиугольные ортобикуполы удлиненная пятиугольная гиробикупола удлиненная пятиугольная орто-куполаротонда удлиненная пятиугольная гирокуполаротонда удлиненная пятиугольная ортобиротонда удлиненная пятиугольная гиробиротонда гиродлинно-треугольная двуполая гиродлинная квадратная двуполая гировидная пятиугольная двуполая гировидная пятиугольная куполаротонда гировидная пятиугольная биротонда
Дополненный призмы	увеличенная треугольная призма двуугловая треугольная призма трехугольная призма увеличенная пятиугольная призма двуугловая пятиугольная призма увеличенная шестиугольная призма парабиаугментированная шестиугольная призма метабиауглеродная шестиугольная призма трехкратная шестиугольная призма
Изменено Платоновы тела	расширенный додекаэдр парабиаугментированный додекаэдр метабиауглеродный додекаэдр триаугментированный додекаэдр икосаэдр с уменьшенным метабидом трехуменьшенный икосаэдр трижды уменьшенный икосаэдр
Изменено Архимедовы тела	расширенный усеченный тетраэдр увеличенный усеченный куб двунаправленный усеченный куб дополненный усеченный додекаэдр парабиаугментированный усеченный додекаэдр усеченный метабиауглеродный додекаэдр усеченный додекаэдр спиральный ромбикосододекаэдр парабигиратный ромбикосододекаэдр метабигиратный ромбикосододекаэдр трехгранный ромбикосододекаэдр уменьшенный ромбикосододекаэдр парагират уменьшенный ромбикосододекаэдр метагират уменьшенный ромбикосододекаэдр бигират уменьшенный ромбикосододекаэдр парабидоусиленный ромбоикосододекаэдр метабидоусиленный ромбикосододекаэдр вращающийся двумерный ромбикосододекаэдр трехкоординатный ромбоикосододекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона увеличенная сфенокорона сфеномегакорона Hebesphenomegacorona дифеноцингулум билунабиротонда треугольная гебесфеноротунда
(Смотрите также Список твердых тел Джонсона, сортируемая таблица)