Купол (геометрия) - Cupola (geometry)

Для использования в других целях см. Купол (значения).

Набор куполов

Пятиугольный купол (пример)
Символ Шлефли	{п} || t {п}
Лица	п треугольники, п квадраты, 1 п-угольник, 1 2п-угольник
Края	5п
Вершины	3п
Группа симметрии	Cпv, [1,п], (*nn), порядок 2n
Группа вращения	Cп, [1,п]^+, (nn), заказ n
Двойной	?
Свойства	выпуклый

В геометрия, а купол твердое тело, образованное соединением двух полигоны, одно (основание) с вдвое большим количеством ребер, чем другое, чередующейся полосой равнобедренных треугольники и прямоугольники. Если треугольники равносторонний а прямоугольники квадраты, а основание и его противоположная грань - правильные многоугольники, то треугольный, квадрат, и пятиугольник все купола относятся к Твердые тела Джонсона, и может быть сформирован путем взятия участков кубооктаэдр, ромбокубооктаэдр, и ромбоикосододекаэдр соответственно.

Купол можно рассматривать как призма где один из полигонов был свернут пополам путем слияния чередующихся вершин.

Купол можно придать расширенному Символ Шлефли {п} || t {п}, представляющий правильный многоугольник {n}, соединенный параллелью своих усечение, t {n} или {2n}.

Купола являются подклассом призматоиды.

Его двойник имеет форму, которая представляет собой сварной шов между половиной п-сторонний трапецоэдр и 2n-сторонний пирамида.

Примеры

Семейство выпуклых купола

[

• v
• т
• е

]

п	2	3	4	5	6
имя	{2} || т {2}	{3} || т {3}	{4} || т {4}	{5} || т {5}	{6} || т {6}
Купол	Дигональный купол	Треугольный купол	Квадратный купол	Пятиугольный купол	Шестиугольный купол (Плоский)
Связанный униформа многогранники	Треугольная призма	Кубокта- эдр	Ромбовидный кубокта- эдр	Ромб- икосидодека эдр	Ромбовидный трехгексагональный черепица

Самолет "шестиугольник купола »в ромбитогексагональная черепица

Вышеупомянутые три многогранника - единственные нетривиальные выпуклые купола с правильными гранями: "шестиугольник купол »- плоская фигура, а треугольная призма можно рассматривать как «купол» степени 2 (купол отрезка и квадрата). Однако купола многоугольников более высокой степени могут быть построены с помощью нерегулярный треугольные и прямоугольные грани.

Координаты вершин

У 40-гранного купола 40 равнобедренных треугольников (синие), 40 прямоугольников (желтые), верхний правильный 40-угольник (красный) и нижний обычный 80-угольник (скрыто).

Определение купола не требует, чтобы основание (или сторона, противоположная основанию, которую можно назвать вершиной), было правильным многоугольником, но удобно рассмотреть случай, когда купол имеет максимальную симметрию, C_пv. В этом случае верх - обычный п-угольник, а база либо обычная 2п-угольник или 2п-угольник с двумя чередующимися сторонами разной длины и такими же углами, как у обычного 2п-гон. Систему координат удобно закрепить так, чтобы основание лежало в ху-плоскость с вершиной в плоскости, параллельной плоскости ху-самолет. В zось - это пось складывания, а плоскости зеркал проходят через z-оси и разделите пополам стороны основания. Они также либо делят пополам стороны или углы верхнего многоугольника, либо и то, и другое. (Если п ровно, половина зеркальных плоскостей делит пополам стороны верхнего многоугольника и половину пополам углы, а если п нечетно, каждая зеркальная плоскость делит пополам одну сторону и один угол верхнего многоугольника.) Вершины основания можно обозначить как V₁ через V_2п, а вершины верхнего многоугольника обозначим V_2п+1 через V_3п. С этими соглашениями координаты вершин можно записать как:

• V_2j−1: (р_б cos [2π (j − 1) / п + α], р_б грех [2π (j − 1) / п + α], 0)
• V_2j: (р_б cos (2πj / п - α), р_б грех (2πj / п - α), 0)
• V_2п+j: (р_т cos (πj / п), р_т грех (πj / п), час)

где j = 1, 2, ..., п.

Поскольку многоугольники V₁V₂V_2п+2V_2п+1и т. д. являются прямоугольниками, это накладывает ограничение на значения р_б, р_т, и α. Расстояние V₁V₂ равно

р_б{[cos (2π / п - α) - cos α]² + [sin (2π / п - α) - sin α]²}^1/2

= р_б{[cos²(2π / п - α) - 2cos (2π / п - α) cos α + cos² α] + [грех²(2π / п - α) - 2sin (2π / п - α) грех α + грех² α]}^1/2

= р_б{2 [1 - cos (2π / п - α) cos α - sin (2π / п - α) грех α]}^1/2

= р_б{2 [1 - cos (2π / п - 2α)]}^1/2

в то время как расстояние V_2п+1V_2п+2 равно

р_т{[cos (π / п) − 1]² + грех²(π / п)}^1/2

= р_т{[cos²(π / п) - 2cos (π / п) + 1] + грех²(π / п)}^1/2

= р_т{2 [1 - cos (π / п)]}^1/2.

Они должны быть равны, и если это общее ребро обозначить s,

р_б = s / {2 [1 - cos (2π / n - 2α)]}^1/2

р_т = s / {2 [1 - cos (π / п)]}^1/2

Эти значения должны быть вставлены в выражения для координат вершин, приведенные ранее.

Звезда-купола

Семья звездные купола

п / d	4	5	7	8
3	{4/3}	{5/3}	{7/3}	{8/3}
5	—	—	{7/5}	{8/5}

Семейство звездчатых куплоидов

​п⁄d	3	5	7
2	Перекрещенный треугольный куплоид	Пентаграмматический куплоид	Гептаграмматический куплоид
4	—	Перекрещенный пятиугольный куплоид	Скрещенный гептаграммный куплоид

Звездные купола существуют для всех баз {п/d} где ⁶/₅ < ^п/_d <6 и d странно. В пределах границ купола сжимаются в плоские фигуры: вне пределов треугольники и квадраты больше не могут перекрывать расстояние между двумя многоугольниками. Когда d четное, нижнее основание {2п/d} становится вырожденным: мы можем сформировать куплоид или полукупола убрав это выродившееся лицо и позволив треугольникам и квадратам соединиться здесь друг с другом. В частности, тетрагемигексаэдр можно рассматривать как {3/2} -куплоид. Купола все ориентируемый, а все куплоиды неориентируемы. Когда п/d > 2 в куплоиде треугольники и квадраты не покрывают все основание, а в основании остается небольшая мембрана, которая просто закрывает пустое пространство. Следовательно, куплоиды {5/2} и {7/2}, изображенные выше, имеют мембраны (незаполненные), а куплоиды {5/4} и {7/4}, изображенные выше, не имеют.

Высота час из {п/d} -купола или куплоид определяется по формуле${\displaystyle h={\sqrt {1-{\frac {1}{4\sin ^{2}({\frac {\pi d}{n}})}}}}}$. Особенно, час = 0 в пределах п/d = 6 и п/d = 6/5, и час максимизируется на п/d = 2 (треугольная призма, где треугольники расположены вертикально).^[1][2]

На изображениях выше звездные купола имеют последовательную цветовую схему, чтобы помочь идентифицировать их лица: основание п/d-угольник красный, основание 2n/d-угольник желтый, квадраты синие, а треугольники зеленые. Куплоиды имеют основу п/d-угольник красный, квадраты желтые и треугольники синие, так как другая база была удалена.

Антикупола

Набор антикупол

Пятиугольный пример
Символ Шлефли	s {п} || t {п}
Лица	3п треугольники 1 п-угольник, 1 2п-угольник
Края	6п
Вершины	3п
Группа симметрии	Cпv, [1,п], (*nn), порядок 2п
Группа вращения	Cп, [1,п]^+, (nn), порядок п
Двойной	?
Свойства	выпуклый

An п-гональный антикупола строится из регулярных 2п-огональная база, 3п треугольников двух типов, а обычный п-кональный верх. Для п = 2, верхняя грань двуугольника сводится к единственному ребру. Вершины верхнего многоугольника выровнены с вершинами нижнего многоугольника. Симметрия C_пv, порядок 2п.

Антикупола не может быть построена со всеми правильными гранями,^{[нужна цитата ]} хотя некоторые можно сделать штатными. Если верх п-угольник и треугольники правильные, основание 2п-гон не может быть планарным и правильным. В таком случае, п= 6 образует правильный шестиугольник и окружающие равносторонние треугольники плоская шестиугольная черепица, который может быть замкнут в многоугольник нулевого объема с основанием в виде симметричного 12-угольника в форме большего шестиугольника, имеющего смежные пары коллинеарный края.

Две антикуполы могут быть увеличены вместе на их основе как биантикупола.

Семейство выпуклых антикупол

п	2	3	4	5	6...
имя	с {2} || т {2}	с {3} || т {3}	с {4} || т {4}	с {5} || т {5}	с {6} || т {6}
Образ	Дигональный	Треугольная	Квадрат	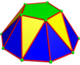Пятиугольник	Шестиугольный
Прозрачный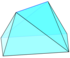
Сеть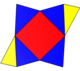

Hypercupolae

В гиперкупола или многогранные купола представляют собой семейство выпуклых неоднородных полихор (здесь четырехмерных фигур), аналогичных куполам. Каждая база - это Платоново твердое тело и это расширение.^[3]

имя	Тетраэдрический купол		Кубический купол		Восьмигранный купол		Додекаэдрический купол		Купол из шестиугольной черепицы
Символ Шлефли	{3,3} || рр {3,3}		{4,3} || рр {4,3}		{3,4} || рр {3,4}		{5,3} || рр {5,3}		{6,3} || рр {6,3}
Сегментохора показатель[3]	K4.23		K4.71		K4.107		K4.152
по окружности	1		sqrt ((3 + sqrt (2)) / 2) = 1.485634		sqrt (2 + sqrt (2)) = 1.847759		3 + sqrt (5) = 5.236068
Образ
Клетки крышки
Вершины	16		32		30		80		∞
Края	42		84		84		210		∞
Лица	42	24 {3} + 18 {4}	80	32 {3} + 48 {4}	82	40 {3} + 42 {4}	194	80 {3} + 90 {4} + 24 {5}	∞
Клетки	16	1 тетраэдр 4 треугольные призмы 6 треугольные призмы 4 треугольные пирамиды 1 кубооктаэдр	28	1 куб  6 квадратные призмы 12 треугольные призмы  8 треугольные пирамиды  1 ромбокубооктаэдр	28	1 октаэдр  8 треугольные призмы 12 треугольные призмы  6 квадратные пирамиды 1 ромбокубооктаэдр	64	1 додекаэдр 12 пятиугольные призмы 30 треугольные призмы 20 треугольные пирамиды  1 ромбикосододекаэдр	∞	1 шестиугольная плитка ∞ шестиугольные призмы ∞ треугольных призм ∞ треугольных пирамид 1 ромбогексагональная черепица
Связанный униформа полихора	5-клеточный		беглый тессеракт		беглый 24-элементный		беглый 120-клеточный		многослойная шестиугольная черепица с сотовой структурой

Смотрите также

• Ортобикупола
• Гиробикупола
• Ротонда

использованная литература

1. "купола". www.orchidpalms.com. Получено 21 апреля 2018.
2. "полукупола". www.orchidpalms.com. Получено 21 апреля 2018.
3. Выпуклый сегментохора Д-р Ричард Клитцинг, Симметрия: культура и наука, Vol. 11, №№ 1–4, 139–181, 2000 г.

• Джонсон, Н.В. Выпуклые многогранники с правильными гранями. Мочь. J. Math. 18, 169–200, 1966.

внешние ссылки

• Вайсштейн, Эрик В. "Купол". MathWorld.
• Сегментотопы