Скрещенный квадратный купол - Crossed square cupola
| Скрещенный квадратный купол | |
|---|---|
 | |
| Тип | Джонсон изоморф Купол |
| Лица | 4 треугольники 1+4 квадраты 1 октаграмма |
| Края | 20 |
| Вершины | 12 |
| Конфигурация вершины | 4+4(3.4.8/3) 4(3/2.43) |
| Символ Шлефли | {4/3} || т {4/3} |
| Группа симметрии | C4в, [4], (*44) |
| Группа вращения | C4, [4]+, (44) |
| Двойной многогранник | - |
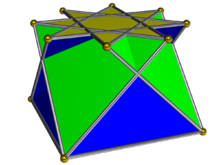
В геометрия, то скрещенный квадратный купол один из невыпуклых Твердые изоморфы Джонсона, топологически тождественная выпуклой квадратный купол. Его можно получить как кусок невыпуклый большой ромбокубооктаэдр или квазиромбокубооктаэдр. Как и во всех купола, база многоугольник вдвое больше края и вершины как верхний; в этом случае базовый многоугольник является октаграмма.
Его можно рассматривать как купол с ретроградным квадратным основанием, так что квадраты и треугольники соединяются через основания противоположно квадратному куполу, следовательно, пересекаются друг с другом.
Связанные многогранники
| п / d | 4 | 5 | 7 | 8 |
|---|---|---|---|---|
| 3 |  {4/3} |  {5/3} |  {7/3} |  {8/3} |
| 5 | — | — |  {7/5} |  {8/5} |
Перекрещенный квадратный купол можно рассматривать как часть неких однородных многогранников. Например, большой кубокубооктаэдр можно рассматривать как шесть скрещенных квадратных куполов, соединенных своими треугольными гранями, в то время как невыпуклый большой ромбокубооктаэдр можно рассматривать как смесь шести куполов. Кроме того, невыпуклый большой ромбокубооктаэдр можно рассматривать как восьмиугольная призма с октаграммами, выкопанными с перекрещенными квадратными куполами, подобно тому, как ромбокубооктаэдр можно рассматривать как восьмиугольная призма с восьмиугольниками, дополненными квадратными куполами. Вращение одного из куполов в этой конструкции приводит к псевдо-большой ромбокубооктаэдр. К этому можно добавить большой ромбогексаэдр, как исключение или всех трех из этих октаграммных призм, которые могут быть использованы для построения невыпуклого большого ромбокубооктаэдра.
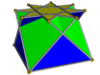 Скрещенный квадратный купол |  Невыпуклый большой ромбокубооктаэдр |  Псевдо-большой ромбокубооктаэдр |  Большой кубокубооктаэдр |  Большой ромбогексаэдр |
На фотографиях ниже показаны раскопки октаграмматической призмы со скрещенными квадратными куполами, происходившие шаг за шагом. Перекрещенные квадратные купола всегда красного цвета, в то время как квадратные стороны восьмиугольной призмы - другого цвета. Все изображения ориентированы примерно одинаково для наглядности.
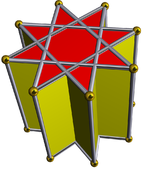 Октаграммная призма (окрашена D8ч симметрия) ... | 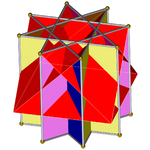 ... с выкопанной одной из октаграмм (здесь верхняя) с перекрещенным квадратным куполом. Это можно назвать ретро-удлиненный скрещенный квадратный купол или же увеличенная октаграммная призма, и изоморфен Джонсону удлиненный квадратный купол. | 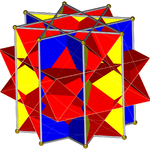 Есть два варианта ориентации другого перекрещенного квадратного купола. Один совмещает соответствующие грани (треугольники с треугольниками, квадраты с квадратами) и дает невыпуклый большой ромбокубооктаэдр. Эта конструкция имеет D4ч симметрии, хотя невыпуклый большой ромбокубооктаэдр имеет полный октаэдрическая симметрия. | 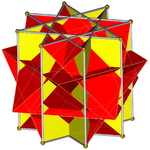 Другой выбор выравнивает несовпадающие грани (треугольники с квадратами) и создает псевдо-большой ромбокубооктаэдр (или псевдоквазиромбокубооктаэдр). Эта конструкция имеет D4d симметрия. |
Эту серию раскопок легко сравнить с соответствующей серией увеличений восьмиугольной призмы:
 Восьмиугольная призма (окрашена D8ч симметрия) ... | 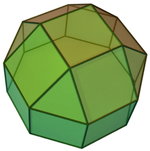 ... с одним из восьмиугольников, дополненным квадратным куполом. |  Есть два варианта ориентации другого перекрещенного квадратного купола. Один совмещает соответствующие грани (треугольники с треугольниками, квадраты с квадратами) и дает ромбокубооктаэдр. Эта конструкция имеет D4ч симметрия, хотя ромбокубооктаэдр имеет полную октаэдрическую симметрию. | 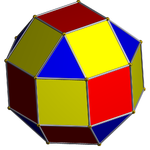 Другой выбор выравнивает несоответствующие грани (треугольники с квадратами) и производит псевдоромбокубооктаэдр. Эта конструкция имеет D4d симметрия. |
Двойной многогранник
Двойной скрещенный квадратный купол имеет 8 треугольных и 4 лица змея:

За счет проходящих близко к центру граней скрещенного квадратного купола этот дуал очень остроконечный по внешнему виду. Это также происходит для двойственных однородных многогранников, известных как додекаэдр большой пентаки (DU58) и средний перевернутый пятиугольный шестигранник (DU60).
Рекомендации
- Джим Макнил, Купол ИЛИ Семикупола
- Джим Макнил, Связь куполов с однородными многогранниками.
