Равномерный многогранник - Uniform polyhedron

Платоново твердое тело: Тетраэдр

Равномерный звездный многогранник: Курносый додекадодекаэдр

А униформа многогранник имеет правильные многоугольники в качестве лица и является вершинно-транзитивный (т.е. существует изометрия отображение любой вершины на любую другую). Отсюда следует, что все вершины конгруэнтный.

Униформа многогранники могут быть обычный (если также грань и ребро транзитивны), квазирегулярный (если также ребро транзитивно, но не грань транзитивно), или полурегулярный (если ни ребро, ни грань не транзитивны). Грани и вершины не обязательно выпуклый, поэтому многие однородные многогранники тоже звездные многогранники.

Есть два бесконечных класса однородных многогранников вместе с 75 другими многогранниками:

• Бесконечные классы:
  • призмы,
  • антипризмы.
• Выпуклые исключительные:
  • 5 Платоновы тела: правильные выпуклые многогранники,
  • 13 Архимедовы тела: 2 квазирегулярный и 11 полуправильный выпуклые многогранники.
• Звездочка (невыпуклая) исключительная:
  • 4 Многогранники Кеплера – Пуансо: правильные невыпуклые многогранники,
  • 53 однородные звездные многогранники: 5 квазирегулярный и 48 полурегулярных.

Следовательно, 5 + 13 + 4 + 53 = 75.

Есть также много вырожденных однородных многогранников с совпадающими парами ребер, в том числе один, найденный Джоном Скиллингом и названный большой дизнуб диргомбидодекаэдр (Фигура Скиллинга).

Двойные многогранники однородным многогранникам лицо переходный (равногранный) и имеют регулярные фигуры вершин, и обычно классифицируются параллельно их двойственному (однородному) многограннику. Двойственный к правильному многограннику является правильным, а двойственный к архимедовому телу - Каталонский твердый.

Понятие равномерного многогранника является частным случаем понятия равномерный многогранник, что также применимо к фигурам в многомерном (или низкоразмерном) пространстве.

Определение

Первородный грех в теории многогранников восходит к Евклиду, и через Кеплера, Пуансо, Коши и многих других продолжает поражать все работы по этой теме (включая работу автора настоящей статьи). Это происходит из-за того, что традиционное использование термина «правильные многогранники» противоречило и остается вопреки синтаксису и логике: эти слова, кажется, подразумевают, что мы имеем дело среди объектов, которые мы называем «многогранники», с теми особенными те, которые заслуживают называться «обычными». Но на каждом этапе - Евклид, Кеплер, Пуансо, Гесс, Брюкнер… - авторам не удавалось определить, что такое «многогранники», среди которых они находят «правильные».

(Бранко Грюнбаум1994 )

Коксетер, Лонге-Хиггинс и Миллер (1954) Определим однородные многогранники как вершинно-транзитивные многогранники с правильными гранями. Они определяют многогранник как конечный набор многоугольников, так что каждая сторона многоугольника является стороной только одного другого многоугольника, так что ни одно непустое собственное подмножество многоугольников не обладает таким же свойством. Под многоугольником они неявно подразумевают многоугольник в трехмерном евклидовом пространстве; они могут быть невыпуклыми и пересекать друг друга.

Есть некоторые обобщения понятия равномерного многогранника. Если отказаться от предположения о связности, то мы получим однородные соединения, которые можно разбить как объединение многогранников, например, соединение пяти кубиков. Если отказаться от условия невырожденности реализации многогранника, мы получим так называемые вырожденные однородные многогранники. Это требует более общего определения многогранников. Грюнбаум (1994) дал довольно сложное определение многограннику, а Макмаллен и Шульте (2002) дали более простое и общее определение многогранника: в их терминологии многогранник - это двумерный абстрактный многогранник с невырожденной 3-мерной реализацией. Здесь абстрактный многогранник - это совокупность его «граней», удовлетворяющих различным условиям, реализация - это функция от ее вершин до некоторого пространства, и реализация называется невырожденной, если любые две различные грани абстрактного многогранника имеют различные реализации. Вот некоторые из способов, которыми они могут быть вырождены:

• Скрытые лица. Некоторые многогранники имеют скрытые грани в том смысле, что их внутренние части не видны снаружи. Обычно они не считаются однородными многогранниками.
• Вырожденные соединения. Некоторые многогранники имеют несколько ребер, и их грани являются гранями двух или более многогранников, хотя они не являются составными в предыдущем смысле, поскольку многогранники имеют общие ребра.
• Двойные крышки. Существуют неориентируемые многогранники с двойными покрытиями, удовлетворяющие определению равномерного многогранника. У двойных крышек двойные грани, ребра и вершины. Обычно они не считаются однородными многогранниками.
• Двойные лица. Есть несколько многогранников с удвоенными гранями, образованных конструкцией Витхоффа. Большинство авторов не допускают сдвоения граней и убирают их как часть конструкции.
• Двойные края. Фигура Скиллинга имеет двойные ребра (как в вырожденных однородных многогранниках), но ее грани нельзя записать как объединение двух однородных многогранников.

История

Правильные выпуклые многогранники

• В Платоновы тела восходят к классическим грекам и изучались Пифагорейцы, Платон (ок. 424 - 348 г. до н.э.), Theaetetus (ок. 417 г. до н.э. - 369 г. до н.э.), Тимей Локровский (ок. 420–380 до н. э.) и Евклид (эт. 300 г. до н. э.). В Этруски открыл правильный додекаэдр до 500 г. до н.э.^[1]

Неправильные равномерные выпуклые многогранники

• В кубооктаэдр был известен Платон.
• Архимед (287 г. до н.э. - 212 г. до н.э.) открыл все 13 Архимедовы тела. Его оригинальная книга по этому вопросу была утеряна, но Папп Александрийский (ок. 290 - ок. 350 н. э.) упомянул, что Архимед перечислил 13 многогранников.
• Пьеро делла Франческа (1415 - 1492) заново открыл пять усеченных Платоновых тел: усеченный тетраэдр, усеченный октаэдр, усеченный куб, усеченный додекаэдр и усеченный икосаэдр, и включил в свою книгу иллюстрации и расчеты их метрических свойств. De quinque corporibus regularibus. Он также обсуждал кубооктаэдр в другой книге.^[2]
• Лука Пачоли плагиатом работы Франчески в De Divina пропорционально в 1509 г., добавив ромбокубооктаэдр, называя это икосигексаэдр для его 26 граней, которые были нарисованы Леонардо да Винчи.
• Иоганн Кеплер (1571–1630) был первым, кто опубликовал полный список Архимедовы тела, в 1619 г., а также выявили бесконечные семейства униформ призмы и антипризмы.

Правильные звездные многогранники

• Кеплер (1619) открыл два регулярных Многогранники Кеплера – Пуансо и Луи Пуансо (1809) открыл два других. Набор из четырех был доказан Огюстен Коши (1789 - 1857) и назван Артур Кэли (1821 – 1895).

Другие 53 нерегулярных звездных многогранника

• Из оставшихся 53, Эдмунд Гесс (1878) открыл два, Альберт Бадуро (1881) открыл еще 36, а Питч (1881) независимо открыл 18, из которых 3 ранее не были обнаружены. Вместе они дали 41 многогранник.
• Геометр H.S.M. Coxeter обнаружил оставшиеся двенадцать в сотрудничестве с Дж. С. П. Миллер (1930–1932), но не публиковал. РС. Лонге-Хиггинс и H.C. Лонге-Хиггинс независимо обнаружил одиннадцать из них. Пятеро из них были заново открыты Лесавром и Мерсье в 1947 году.
• Коксетер, Лонге-Хиггинс и Миллер (1954) опубликовал список равномерных многогранников.
• Сопов (1970) доказали свою гипотезу о том, что список был полным.
• В 1974 г. Магнус Веннингер опубликовал свою книгу Модели многогранников, в котором перечислены все 75 непризматических однородных многогранников со многими ранее неопубликованными именами, данными им Норман Джонсон.
• Мастерство (1975) независимо доказал полноту и показал, что если определение равномерного многогранника ослабить, чтобы рёбра совпадали, то есть только одна дополнительная возможность.
• В 1987 г. Эдмонд Бонан нарисовал все однородные многогранники и их двойники в 3D с помощью программы Turbo Pascal под названием Полика: почти из них были показаны во время Международного конгресса стереоскопического союза, который проходил в Конгресс-театре, Истборн, Великобритания.^{[нужна цитата ]}.^[3]
• В 1993 году Цви Хар'Эль произвел полное калейдоскопическое построение однородных многогранников и двойников с помощью компьютерной программы под названием Калейдо, и резюмировано в статье Равномерное решение для равномерных многогранников., считая цифры 1-80.^[4]
• Также в 1993 году Р. Мадер перенес это решение Kaleido на Mathematica с немного другой системой индексации.^[5]
• В 2002 году Питер В. Мессер открыл минимальный набор выражений в замкнутой форме для определения основных комбинаторных и метрических величин любого однородного многогранника (и двойственного к нему), учитывая только его Символ Wythoff.^[6]

Однородные звездные многогранники

Основная статья: Равномерный звездный многогранник

Большой диромбикосододекаэдр, единственный однородный многогранник, не относящийся к Витоффу.

57 непризматических невыпуклых форм, за исключением большой диромбикосододекаэдр, компилируются конструкциями Wythoff в Треугольники Шварца.

Выпуклые формы по конструкции Wythoff

Выпуклые равномерные многогранники можно назвать Строительство Wythoff операции по обычной форме.

Более подробно выпуклые однородные многогранники приведены ниже по их конструкции Уайтхоффа в каждой группе симметрии.

В конструкции Wythoff есть повторения, созданные формами более низкой симметрии. Куб - это правильный многогранник и квадратная призма. В октаэдр - правильный многогранник и треугольная антипризма. В октаэдр также выпрямленный тетраэдр. Многие многогранники повторяются из разных источников построения и окрашиваются по-разному.

Конструкция Wythoff одинаково применима к однородным многогранникам и однородные мозаики на поверхности сферы, поэтому даны изображения обоих. Сферические мозаики, включающие множество осоэдры и дигедры которые являются вырожденными многогранниками.

Эти группы симметрии образуются из отражающих группы точек в трех измерениях, каждый из которых представлен фундаментальным треугольником (п q р), куда п > 1, q > 1, р > 1 и 1/п + 1/q + 1/р < 1.

• Тетраэдрическая симметрия (3 3 2) - заказ 24
• Октаэдрическая симметрия (4 3 2) - заказ 48
• Икосаэдрическая симметрия (5 3 2) - заказ 120
• Двугранная симметрия (п 2 2), для п = 3,4,5, ... - порядок 4п

Остальные неотражающие формы строятся чередование операции над многогранниками с четным числом сторон.

Наряду с призмами и их двугранная симметрия, процесс построения сферической Wythoff добавляет два обычный классы, которые становятся вырожденными как многогранники: дигедра и Hosohedra, у первого только две грани, а у второго - только две вершины. Усечение регулярного Hosohedra создает призмы.

Ниже выпуклые однородные многогранники имеют номера 1–18 для непризматических форм, как они представлены в таблицах по форме симметрии.

Для бесконечного множества призматических форм они разделены на четыре семейства:

1. Хосоэдра ЧАС_2... (только как сферические мозаики)
2. Дигедра D_2... (только как сферические мозаики)
3. Призмы п_3... (усеченные осоэдры)
4. Антипризмы А_3... (курносые призмы)

Сводные таблицы

Джонсон имя	Родитель	Усеченный	Исправленный	Bitruncated (тр. двойной)	Двунаправленный (двойной)	Собранный	Усеченный (усеченный)	Курносый
Диаграмма Кокстера
Расширенный Символ Шлефли	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$
	{p, q}	т {р, д}	г {р, д}	2t {p, q}	2r {p, q}	рр {р, q}	tr {p, q}	sr {p, q}
	т0{p, q}	т0,1{p, q}	т1{p, q}	т1,2{p, q}	т2{p, q}	т0,2{p, q}	т0,1,2{p, q}	ht0,1,2{p, q}
Символ Wythoff (p q 2)	q | п 2	2 q | п	2 | p q	2 п | q	p | q 2	p q | 2	p q 2 |	| p q 2
Фигура вершины	п^q	q.2p.2p	(p.q)^2	p.2q.2q	q^п	стр.4.q.4	4.2p.2q	3.3.p.3.q
Тетраэдр (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
Восьмигранный (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
Икосаэдр (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

И пример двугранной симметрии:

(Сфера не разрезается, разрезается только мозаика.) (На сфере ребро - это дуга большого круга, кратчайшего пути между двумя его вершинами. Следовательно, двуугольник, вершины которого не полярно-противоположны, называется плоский: похоже на край.)

(стр 2 2)	Родитель	Усеченный	Исправленный	Bitruncated (тр. двойной)	Двунаправленный (двойной)	Собранный	Усеченный (усеченный)	Курносый
Диаграмма Кокстера
Расширенный Символ Шлефли	${\displaystyle {\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\2\end{Bmatrix}}}$
	{p, 2}	т {р, 2}	г {р, 2}	2t {p, 2}	2р {п, 2}	рр {р, 2}	tr {p, 2}	ст {р, 2}
	т0{p, 2}	т0,1{p, 2}	т1{p, 2}	т1,2{p, 2}	т2{p, 2}	т0,2{p, 2}	т0,1,2{p, 2}	ht0,1,2{p, 2}
Символ Wythoff	2 | п 2	2 2 | п	2 | п 2	2 п | 2	p | 2 2	п 2 | 2	п 2 2 |	| стр 2 2
Фигура вершины	п^2	2.2п. 2п	п.2.п.2	п.4.4	2^п	п.4.2.4	4.2p.4	3.3.3.p
Двугранный (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
Двугранный (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	4.4.6	3.3.3.3
Двугранный (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	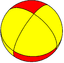3.3.3.4
Двугранный (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	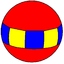4.4.10	3.3.3.5
Двугранный (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

(3 3 2) т_d тетраэдрическая симметрия

В тетраэдрическая симметрия сферы образует 5 однородных многогранников и 6-ю форму с помощью операции курноса.

Тетраэдрическая симметрия представлена ​​фундаментальным треугольником с одной вершиной с двумя зеркалами и двумя вершинами с тремя зеркалами, представленными символом (3 3 2). Он также может быть представлен Группа Коксетера А₂ или [3,3], а также Диаграмма Кокстера: .

24 треугольника, видимых на гранях тетракис шестигранник, и в треугольниках на сфере чередования цветов:

#	Имя	График А3	График А2	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
								Поз. 2 [3] (4)	Поз. 1 [2] (6)	Поз. 0 [3] (4)	Лица	Края	Вершины
1	Тетраэдр						{3,3}	{3}			4	6	4
[1]	Двунаправленный тетраэдр (такой же как тетраэдр )						т2{3,3}={3,3}			{3}	4	6	4
2	Выпрямленный тетраэдр Тетратетраэдр (такой же как октаэдр )						т1{3,3} = r {3,3}	{3}		{3}	8	12	6
3	Усеченный тетраэдр						т0,1{3,3} = t {3,3}	{6}		{3}	8	18	12
[3]	Усеченный тетраэдр (такой же как усеченный тетраэдр )						т1,2{3,3} = t {3,3}	{3}		{6}	8	18	12
4	Кантеллированный тетраэдр Ромбитратратраэдр (такой же как кубооктаэдр )						т0,2{3,3} = rr {3,3}	{3}	{4}	{3}	14	24	12
5	Омнитусеченный тетраэдр Усеченный тетратетраэдр (такой же как усеченный октаэдр )						т0,1,2{3,3} = tr {3,3}	{6}	{4}	{6}	14	36	24
6	Курносый тетратетраэдр (такой же как икосаэдр )		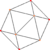				ср {3,3}	{3}	2 {3}	{3}	20	30	12

(4 3 2) O_час октаэдрическая симметрия

В октаэдрическая симметрия сферы образует 7 однородных многогранников и еще 7 путем чередования. Шесть из этих форм повторяются из таблицы симметрии тетраэдра выше.

Октаэдрическая симметрия представлена ​​фундаментальным треугольником (4 3 2), в каждой вершине которого считаются зеркала. Он также может быть представлен Группа Коксетера B₂ или [4,3], а также Диаграмма Кокстера: .

48 треугольников, видимых на гранях disdyakis додекаэдр, а также в треугольниках на сфере чередования цветов:

#	Имя	График B3	График B2	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
								Поз. 2 [4] (6)	Поз. 1 [2] (12)	Поз. 0 [3] (8)	Лица	Края	Вершины
7	Куб						{4,3}	{4}			6	12	8
[2]	Октаэдр						{3,4}			{3}	8	12	6
[4]	Ректифицированный куб Выпрямленный октаэдр (Кубооктаэдр )						{4,3}	{4}		{3}	14	24	12
8	Усеченный куб						т0,1{4,3} = t {4,3}	{8}		{3}	14	36	24
[5]	Усеченный октаэдр						т0,1{3,4} = t {3,4}	{4}		{6}	14	36	24
9	Собранный куб Кантеллированный октаэдр Ромбокубооктаэдр						т0,2{4,3} = rr {4,3}	{4}	{4}	{3}	26	48	24
10	Омниусеченный куб Омнитусеченный октаэдр Усеченный кубооктаэдр						т0,1,2{4,3} = tr {4,3}	{8}	{4}	{6}	26	72	48
[6]	Курносый октаэдр (такой же как Икосаэдр )						= s {3,4} = sr {3,3}		{3}	{3}	20	30	12
[1]	Половина куба (такой же как Тетраэдр )						= ч {4,3} = {3,3}	^1/2 {3}			4	6	4
[2]	Кантик куб (такой же как Усеченный тетраэдр )						= час2{4,3} = t {3,3}	^1/2 {6}		^1/2 {3}	8	18	12
[4]	(такой же как Кубооктаэдр )						= рр {3,3}				14	24	12
[5]	(такой же как Усеченный октаэдр )						= tr {3,3}				14	36	24
[9]	Кантик курносый октаэдр (такой же как Ромбокубооктаэдр )						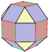s2{3,4} = rr {3,4}				26	48	24
11	Курносый кубооктаэдр						sr {4,3}	{4}	2 {3}	{3}	38	60	24

(5 3 2) Я_час икосаэдрическая симметрия

В икосаэдрическая симметрия сферы образуют 7 однородных многогранников и еще 1 путем чередования. Только один повторяется из таблицы симметрии тетраэдра и октаэдра выше.

Симметрия икосаэдра представлена ​​фундаментальным треугольником (5 3 2), в каждой вершине которого есть зеркала. Он также может быть представлен Группа Коксетера грамм₂ или [5,3], а также Диаграмма Кокстера: .

120 треугольников, видимых на гранях дисьякис триаконтаэдр, и в треугольниках на сфере чередования цветов:

#	Имя	График (А2) [6]	График (ЧАС3) [10]	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
								Поз. 2 [5] (12)	Поз. 1 [2] (30)	Поз. 0 [3] (20)	Лица	Края	Вершины
12	Додекаэдр						{5,3}	{5}			12	30	20
[6]	Икосаэдр						{3,5}			{3}	20	30	12
13	Выпрямленный додекаэдр Исправленный икосаэдр Икосододекаэдр						т1{5,3} = r {5,3}	{5}		{3}	32	60	30
14	Усеченный додекаэдр						т0,1{5,3} = t {5,3}	{10}		{3}	32	90	60
15	Усеченный икосаэдр		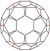				т0,1{3,5} = t {3,5}	{5}		{6}	32	90	60
16	Собранный додекаэдр Скошенный икосаэдр Ромбикосододекаэдр						т0,2{5,3} = rr {5,3}	{5}	{4}	{3}	62	120	60
17	Омниусеченный додекаэдр Омноусеченный икосаэдр Усеченный икосододекаэдр						т0,1,2{5,3} = tr {5,3}	{10}	{4}	{6}	62	180	120
18	Курносый икосододекаэдр						ср {5,3}	{5}	2 {3}	{3}	92	150	60

(p 2 2) Призматический [p, 2], I₂(p) семья (D_пчас двугранная симметрия)

Основная статья: Призматический однородный многогранник

В двугранная симметрия сферы порождает два бесконечных набора однородных многогранников, призм и антипризм, и еще два бесконечных набора вырожденных многогранников, хозоэдров и диэдров, которые существуют как мозаики на сфере.

Двугранная симметрия представлена ​​фундаментальным треугольником (p 2 2) с учетом зеркал в каждой вершине. Он также может быть представлен Группа Коксетера я₂(p) или [n, 2], а также призматический Диаграмма Кокстера: .

Ниже приведены первые пять двугранных симметрий: D₂ ... D₆. Диэдральная симметрия D_п есть заказ 4n, представляли лица бипирамида, а на сфере - линия экватора по долготе и n равноотстоящих линий долготы.

(2 2 2) Двугранная симметрия

На гранях треугольника видно 8 основных треугольников. квадратная бипирамида (Октаэдр) и попеременно раскрашенные треугольники на сфере:

#	Имя	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
						Поз. 2 [2] (2)	Поз. 1 [2] (2)	Поз. 0 [2] (2)	Лица	Края	Вершины
D2 ЧАС2	Дигональный диэдр, двуглавый осоэдр				{2,2}	{2}			2	2	2
D4	Усеченный двугранный двугранник (такой же как квадратный диэдр )				т {2,2} = {4,2}	{4}			2	4	4
п4 [7]	Омнитусеченный двугранный диэдр (такой же как куб )				т0,1,2{2,2} = tr {2,2}	{4}	{4}	{4}	6	12	8
А2 [1]	Курносый двугранный диэдр (такой же как тетраэдр )				ср {2,2}		2 {3}		4	6	4

(3 2 2) D_3ч двугранная симметрия

Есть 12 основных треугольников, видимых на гранях шестиугольная бипирамида и попеременно раскрашенные треугольники на сфере:

#	Имя	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
						Поз. 2 [3] (2)	Поз. 1 [2] (3)	Поз. 0 [2] (3)	Лица	Края	Вершины
D3	Тригональный диэдр				{3,2}	{3}			2	3	3
ЧАС3	Тригональный осоэдр				{2,3}			{2}	3	3	2
D6	Усеченный треугольный диэдр (такой же как шестиугольный диэдр )				т {3,2}	{6}			2	6	6
п3	Усеченный треугольный осоэдр (Треугольная призма )				т {2,3}	{3}	{4}		5	9	6
п6	Омноусеченный трехугольный диэдр (Гексагональная призма )				т0,1,2{2,3} = tr {2,3}	{6}	{4}	{4}	8	18	12
А3 [2]	Курносый тригональный диэдр (такой же как Треугольная антипризма ) (такой же как октаэдр )				ср {2,3}	{3}	2 {3}		8	12	6
п3	Кантик курносый тригональный диэдр (Треугольная призма )				s2{2,3} = t {2,3}				5	9	6

(4 2 2) D_4ч двугранная симметрия

Есть 16 основных треугольников, видимых на гранях восьмиугольная бипирамида и попеременно раскрашенные треугольники на сфере:

#	Имя	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
						Поз. 2 [4] (2)	Поз. 1 [2] (4)	Поз. 0 [2] (4)	Лица	Края	Вершины
D4	квадратный диэдр				{4,2}	{4}			2	4	4
ЧАС4	квадратный осоэдр				{2,4}			{2}	4	4	2
D8	Усеченный квадратный диэдр (такой же как восьмиугольный диэдр )				т {4,2}	{8}			2	8	8
п4 [7]	Усеченный квадратный осоэдр (Куб )				т {2,4}	{4}	{4}		6	12	8
D8	Омнитусеченный квадратный диэдр (Восьмиугольная призма )				т0,1,2{2,4} = tr {2,4}	{8}	{4}	{4}	10	24	16
А4	Плоский квадратный диэдр (Квадратная антипризма )				sr {2,4}	{4}	2 {3}		10	16	8
п4 [7]	Кантик курносый квадратный диэдр (Куб )				s2{4,2} = t {2,4}				6	12	8
А2 [1]	Курносый квадратный осоэдр (Дигональная антипризма ) (Тетраэдр )				s {2,4} = sr {2,2}				4	6	4

(5 2 2) D_5ч двугранная симметрия

Есть 20 основных треугольников, видимых на гранях десятиугольная бипирамида и попеременно раскрашенные треугольники на сфере:

#	Имя	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
						Поз. 2 [5] (2)	Поз. 1 [2] (5)	Поз. 0 [2] (5)	Лица	Края	Вершины
D5	Пятиугольный диэдр				{5,2}	{5}			2	5	5
ЧАС5	Пятиугольный осоэдр				{2,5}			{2}	5	5	2
D10	Усеченный пятиугольный диэдр (такой же как десятиугольный диэдр )				т {5,2}	{10}			2	10	10
п5	Усеченный пятиугольный осоэдр (такой же как пятиугольная призма )				т {2,5}	{5}	{4}		7	15	10
п10	Омнитусеченный пятиугольный диэдр (Десятиугольная призма )				т0,1,2{2,5} = tr {2,5}	{10}	{4}	{4}	12	30	20
А5	Плоский пятиугольный диэдр (Пятиугольная антипризма )				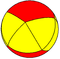ср {2,5}	{5}	2 {3}		12	20	10
п5	Кантик курносый пятиугольный диэдр (Пятиугольная призма )				s2{5,2} = t {2,5}				7	15	10

(6 2 2) D_6ч двугранная симметрия

Есть 24 фундаментальных треугольника, видимых на гранях двенадцатигранная бипирамида и попеременно раскрашенные треугольники на сфере.

#	Имя	Рисунок	Плитка	Вершина фигура	Coxeter и Schläfli символы	Подсчет лиц по положению			Количество элементов
						Поз. 2 [6] (2)	Поз. 1 [2] (6)	Поз. 0 [2] (6)	Лица	Края	Вершины
D6	Шестиугольный диэдр				{6,2}	{6}			2	6	6
ЧАС6	Шестиугольный осоэдр				{2,6}			{2}	6	6	2
D12	Усеченный шестиугольный диэдр (такой же как додекагональный диэдр )				т {6,2}	{12}			2	12	12
ЧАС6	Усеченный шестиугольный осоэдр (такой же как шестиугольная призма )				т {2,6}	{6}	{4}		8	18	12
п12	Омнитусеченный шестиугольный диэдр (Додекагональная призма )				т0,1,2{2,6} = tr {2,6}	{12}	{4}	{4}	14	36	24
А6	Плоский шестиугольный диэдр (Шестиугольная антипризма )				ср {2,6}	{6}	2 {3}		14	24	12
п3	Кантический шестиугольный диэдр (Треугольная призма )				= час2{6,2} = t {2,3}				5	9	6
п6	Кантик курносый шестиугольный диэдр (Гексагональная призма )				s2{6,2} = t {2,6}				8	18	12
А3 [2]	Курносый шестиугольный осоэдр (такой же как Треугольная антипризма ) (такой же как октаэдр )				s {2,6} = sr {2,3}				8	12	6

Строительные операторы Wythoff

Операция	Символ	Coxeter диаграмма	Описание
Родитель	{p, q} т0{p, q}		Любой правильный многогранник или мозаика
Исправленный (р)	г {р, д} т1{p, q}		Края полностью обрезаются на отдельные точки. Теперь у многогранника совмещены грани родительского и двойственного. Многогранники названы по количеству сторон двух правильных форм: {p, q} и {q, p}, как кубооктаэдр для r {4,3} между кубом и октаэдром.
Двунаправленный (2r) (также двойной )	2r {p, q} т2{p, q}		Двунаправленная (дуальная) - это дальнейшее усечение, при котором исходные грани превращаются в точки. Под каждой родительской вершиной формируются новые грани. Количество ребер не изменилось и повернуто на 90 градусов. Биректификацию можно рассматривать как двойственную.
Усеченный (т)	т {р, д} т0,1{p, q}		Каждая исходная вершина обрезается, и пробел заполняется новой гранью. Усечение имеет степень свободы, одно решение которой создает однородный усеченный многогранник. Многогранник имеет свои исходные грани, двойные по сторонам, и содержит грани двойственного.
Bitruncated (2t) (также усеченный двойной)	2t {p, q} т1,2{p, q}		Bitruncation можно рассматривать как усечение двойного. Битусеченный куб - усеченный октаэдр.
Собранный (рр) (Также расширенный )	рр {р, q}		В дополнение к усечению вершин каждое исходное ребро скошенный на их месте появляются новые прямоугольные грани. Единая песня находится на полпути между родительской и дуальной формами. Угловой многогранник называется ромб-r {p, q}, как ромбокубооктаэдр для rr {4,3}.
Cantitruncated (tr) (Также всесторонне усеченный )	tr {p, q} т0,1,2{p, q}		Операции усечения и канелляции применяются вместе, чтобы создать полностью усеченную форму, в которой грани родительского элемента удвоены по сторонам, грани двойника удвоены по сторонам и квадраты, где существовали исходные края.

Чередование операций

Операция	Символ	Coxeter диаграмма	Описание
Курносый ректификованный (SR)	sr {p, q}		Альтернативное песнопение усеченное. Все исходные грани имеют вдвое меньше сторон, а квадраты превращаются в ребра. Так как полностью усеченные формы имеют 3 грани на вершину, формируются новые треугольники. Обычно эти чередующиеся формы огранки после этого слегка деформируются, чтобы снова заканчиваться однородными многогранниками. Возможность последней вариации зависит от степени свободы.
Курносый (ы)	s {p, 2q}		Альтернативное усечение
Кантик пренебрежительный (s2)	s2{p, 2q}
Чередование раскоса (hrr)	чрр {2p, 2q}		Возможно только в однородных мозаиках (бесконечных многогранниках), чередование Например,
Половина (ч)	h {2p, q}		Чередование из , такой же как
Кантик (ч2)	час2{2p, q}		Такой же как
Половинное выпрямление (час)	ч. {2p, 2q}		Возможно только в однородных мозаиках (бесконечных многогранниках), чередование , такой же как или же Например, = или же
Квартал (q)	q {2p, 2q}		Возможно только в однородных мозаиках (бесконечных многогранниках), как и Например, = или же

Смотрите также

• Многогранник
  • Правильный многогранник
  • Квазирегулярный многогранник
  • Полуправильный многогранник
• Список равномерных многогранников
  • Список равномерных многогранников по фигуре вершины
  • Список однородных многогранников по символу Wythoff
  • Список равномерных многогранников треугольником Шварца
• Список твердых тел Джонсона
• Список моделей многогранников Веннингера
• Модель многогранника
• Равномерная черепица
• Равномерные мозаики в гиперболической плоскости
• Псевдо-однородный многогранник
• Список фигур

Примечания

1. Правильные многогранники, стр.13
2. Многогранники Пьеро делла Франческа
3. "Stéréo-Club Français - Галерея: Полиэдр".
4. Хар'Эль, З. Равномерное решение для равномерных многогранников., Geometriae Dedicata 47, 57-110, 1993. Цви Хар'Эль, Программное обеспечение Kaleido, Изображений, двойные изображения
5. Мэдер, Р. Э. Однородные многогранники. Mathematica J. 3, 48-57, 1993. [1]
6. Выражения в замкнутой форме для однородных многогранников и двойников к ним, Питер В. Мессер, Discrete Comput Geom 27: 353–375 (2002).^{[мертвая ссылка ]}

Рекомендации

• Брюкнер, М. Vielecke und vielflache. Theorie und geschichte.. Лейпциг, Германия: Teubner, 1900. [2]
• Кокстер, Гарольд Скотт Макдональд; Лонге-Хиггинс, М.С.; Миллер, Дж. С. П. (1954). «Равномерные многогранники» (PDF). Философские труды Королевского общества A. 246 (916): 401–450. Дои:10.1098 / рста.1954.0003. ISSN  0080-4614. JSTOR  91532. МИСТЕР  0062446.
• Грюнбаум, Б. (1994), «Многогранники с полыми гранями», у Тибора Бистрички; Питер Макмаллен; Рольф Шнайдер; и другие. (ред.), Труды Института перспективных исследований многогранников НАТО: абстрактные, выпуклые и вычислительные, Springer, стр. 43–70, Дои:10.1007/978-94-011-0924-6_3, ISBN  978-94-010-4398-4
• Макмаллен, Питер; Шульте, Эгон (2002), Абстрактные правильные многогранники, Издательство Cambride University Press
• Скиллинг, Дж. (1975). «Комплект однородных многогранников». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки.. 278 (1278): 111–135. Дои:10.1098 / рста.1975.0022. ISSN  0080-4614. JSTOR  74475. МИСТЕР  0365333.
• Сопов, С. П. (1970). «Доказательство полноты списка элементарных однородных многогранников». Украинский Геометрический Сборник (8): 139–156. МИСТЕР  0326550.
• Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN  978-0-521-09859-5.

внешняя ссылка

• Вайсштейн, Эрик В. «Равномерный многогранник». MathWorld.
• Равномерное решение для равномерных многогранников.
• Равномерные многогранники
• Виртуальные многогранники Однородные многогранники
• Галерея однородных многогранников
• Равномерный многогранник - от Wolfram MathWorld Имеет наглядную диаграмму всех 75

Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	Ап	Bп	я2(п) / Dп	E6 / E7 / E8 / F4 / грамм2	ЧАСп
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукуб	132 • 231 • 321
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	142 • 241 • 421
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1k2 • 2k1 • k21	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений