Равномерный 6-многогранник - Uniform 6-polytope
В шестимерный геометрия, а равномерный полипетон[1][2] (или же униформа 6-многогранник) является шестимерным равномерный многогранник. Равномерный полипетон - это вершинно-транзитивный, и все грани находятся равномерные 5-многогранники.
Полный комплект выпуклая однородная полипета не было определено, но большинство из них можно сделать как Конструкции Wythoff из небольшого набора группы симметрии. Эти строительные работы представлены перестановки из кольца из Диаграммы Кокстера-Дынкина. Каждая комбинация хотя бы одного кольца на каждой связанной группе узлов на диаграмме дает равномерный 6-многогранник.
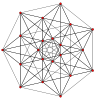
Самыми простыми однородными полипетами являются правильные многогранники: the 6-симплекс {3,3,3,3,3}, 6-куб (шестигранник) {4,3,3,3,3}, а 6-ортоплекс (гексакросс) {3,3,3,3,4}.
История открытия
- Правильные многогранники: (выпуклые грани)
- 1852: Людвиг Шлефли доказано в его рукописи Theorie der vielfachen Kontinuität что есть ровно 3 правильных многогранника в 5 или более размеры.
- Выпуклый полуправильные многогранники: (Различные определения до Кокстера униформа категория)
- 1900: Торольд Госсет перечислил список непризматических полуправильных выпуклых многогранников с правильными фасетами (выпуклые правильные многогранники) в своей публикации О регулярных и полурегулярных фигурах в пространстве n измерений.[3]
- Выпуклые равномерные многогранники:
- 1940: Поиск был систематически расширен H.S.M. Coxeter в своей публикации Правильные и полурегулярные многогранники.
- Неправильные однородные звездные многогранники: (аналогично невыпуклые равномерные многогранники )
- Непрерывный: Известны тысячи невыпуклых однородных полипет, но большинство из них не опубликовано. Предполагается, что список неполный, и нет никакой оценки того, как долго будет полный список, хотя в настоящее время известно более 10000 выпуклых и невыпуклых однородных полипет, в частности 923 с 6-симплексной симметрией. В число участвующих исследователей входят Джонатан Бауэрс, Ричард Клитцинг и Норман Джонсон.[4]
Равномерные 6-многогранники фундаментальными группами Кокстера
Равномерные 6-многогранники с отражательной симметрией могут быть порождены этими четырьмя группами Кокстера, представленными перестановками колец Диаграммы Кокстера-Дынкина.
Есть четыре фундаментальные группы отражающей симметрии, которые порождают 153 уникальных однородных 6-многогранников.
| # | Группа Кокстера | Диаграмма Кокстера-Дынкина | |
|---|---|---|---|
| 1 | А6 | [3,3,3,3,3] | |
| 2 | B6 | [3,3,3,3,4] | |
| 3 | D6 | [3,3,3,31,1] | |
| 4 | E6 | [32,2,1] | |
| [3,32,2] | |||
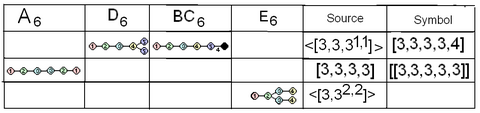 Соответствия диаграмм Кокстера-Дынкина между семействами и высшая симметрия внутри диаграмм. Узлы одного цвета в каждом ряду представляют собой одинаковые зеркала. Черные узлы в переписке не активны. |
Однородные призматические семейства
Равномерная призма
Всего 6 категориальных униформа призмы на основе равномерные 5-многогранники.
| # | Группа Кокстера | Примечания | ||
|---|---|---|---|---|
| 1 | А5А1 | [3,3,3,3,2] | Семейство призм на основе 5-симплекс | |
| 2 | B5А1 | [4,3,3,3,2] | Семейство призм на основе 5-куб | |
| 3а | D5А1 | [32,1,1,2] | Семейство призм на основе 5-полукуб | |
| # | Группа Кокстера | Примечания | ||
|---|---|---|---|---|
| 4 | А3я2(p) А1 | [3,3,2, п, 2] | Семейство призм на основе четырехгранный -p-gonal дуопризма | |
| 5 | B3я2(p) А1 | [4,3,2, п, 2] | Семейство призм на основе кубический -p-gonal дуопризма | |
| 6 | ЧАС3я2(p) А1 | [5,3,2, п, 2] | Семейство призм на основе додекаэдр -p-gonal дуопризма | |
Равномерная дуопризма
Всего 11 категориальных униформа дуопризматический семейства многогранников на основе Декартовы произведения однородных многогранников меньшей размерности. Пять образуются как продукт равномерный 4-многогранник с правильный многоугольник, а шесть образованы произведением двух равномерные многогранники:
| # | Группа Кокстера | Примечания | ||
|---|---|---|---|---|
| 1 | А4я2(п) | [3,3,3,2, p] | Семья на основе 5-элементный -p-гональные дуопризмы. | |
| 2 | B4я2(п) | [4,3,3,2, p] | Семья на основе тессеракт -p-гональные дуопризмы. | |
| 3 | F4я2(п) | [3,4,3,2, п] | Семья на основе 24-элементный -p-гональные дуопризмы. | |
| 4 | ЧАС4я2(п) | [5,3,3,2, p] | Семья на основе 120 ячеек -p-гональные дуопризмы. | |
| 5 | D4я2(п) | [31,1,1, 2, п] | Семья на основе demitesseract -p-гональные дуопризмы. | |
| # | Группа Кокстера | Примечания | ||
|---|---|---|---|---|
| 6 | А32 | [3,3,2,3,3] | Семья на основе четырехгранный дуопризмы. | |
| 7 | А3B3 | [3,3,2,4,3] | Семья на основе четырехгранный -кубический дуопризмы. | |
| 8 | А3ЧАС3 | [3,3,2,5,3] | Семья на основе четырехгранный -додекаэдр дуопризмы. | |
| 9 | B32 | [4,3,2,4,3] | Семья на основе кубический дуопризмы. | |
| 10 | B3ЧАС3 | [4,3,2,5,3] | Семья на основе кубический -додекаэдр дуопризмы. | |
| 11 | ЧАС32 | [5,3,2,5,3] | Семья на основе додекаэдр дуопризмы. | |
Равномерная триапризма
Есть одна бесконечная семья униформа триапризматический семейства многогранников, построенные как Декартовы произведения из трех правильных многоугольников. Каждая комбинация хотя бы одного кольца на каждой связной группе дает однородный призматический 6-многогранник.
| # | Группа Кокстера | Примечания | ||
|---|---|---|---|---|
| 1 | я2(число Пи2(q) Я2(р) | [p, 2, q, 2, r] | Семейство на основе p, q, r-угольных трипризм | |
Перечисление выпуклых равномерных 6-многогранников
- Симплекс семья: A6 [34] -











- 35 равномерных 6-многогранников как перестановок колец в групповой диаграмме, включая один регулярный:
- {34} - 6-симплекс -











- {34} - 6-симплекс -
- 35 равномерных 6-многогранников как перестановок колец в групповой диаграмме, включая один регулярный:
- Гиперкуб /ортоплекс семья: B6 [4,34] -











- 63 равномерных 6-многогранников как перестановки колец в групповой диаграмме, включая две регулярные формы:
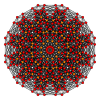
- {4,33} — 6-куб (шестиугольник) -











- {33,4} — 6-ортоплекс, (гексакросс) -











- {4,33} — 6-куб (шестиугольник) -
- 63 равномерных 6-многогранников как перестановки колец в групповой диаграмме, включая две регулярные формы:
- Демигиперкуб D6 семья: [33,1,1] -









- 47 равномерных 6-многогранников (16 уникальных) как перестановки колец в групповой диаграмме, в том числе:
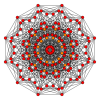
- {3,32,1}, 121 6-полукуб (демигексеракт) -








 ; также как h {4,33},
; также как h {4,33}, 










- {3,3,31,1}, 211 6-ортоплекс -








 , полусимметричная форма
, полусимметричная форма 









 .
.
- {3,32,1}, 121 6-полукуб (демигексеракт) -
- 47 равномерных 6-многогранников (16 уникальных) как перестановки колец в групповой диаграмме, в том числе:
- E6 семья: [33,1,1] -









Эти фундаментальные семейства порождают 153 непризматических выпуклых однородных полипета.
Кроме того, имеется 105 однородных 6-многогранных конструкций на основе призм равномерные 5-многогранники: [3,3,3,3,2], [4,3,3,3,2], [5,3,3,3,2], [32,1,1,2].
Кроме того, существует бесконечно много равномерных 6-многогранников, основанных на:
- Семейства двойных призм: [3,3,2, p, 2], [4,3,2, p, 2], [5,3,2, p, 2].
- Семейства дуопризм: [3,3,3,2, p], [4,3,3,2, p], [5,3,3,2, p].
- Семейство триапризмы: [p, 2, q, 2, r].
А6 семья
Существует 32 + 4−1 = 35 форм, полученных путем маркировки одного или нескольких узлов Диаграмма Кокстера-Дынкина. Все 35 перечислены ниже. Они названы Норман Джонсон из операций построения Wythoff на регулярном 6-симплексе (гептапетон). Названия акронимов в стиле Bowers приведены в скобках для перекрестных ссылок.
А6 семейство имеет симметрию порядка 5040 (7 факториал ).
Координаты однородных 6-многогранников с 6-симплексной симметрией могут быть сгенерированы как перестановки простых целых чисел в 7-пространстве, все в гиперплоскостях с нормальный вектор (1,1,1,1,1,1,1).
| # | Кокстер-Дынкин | Джонсон система именования Имя Bowers и (аббревиатура) | Базовая точка | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | 0 | ||||
| 1 | 6-симплекс гептапетон (хмель) | (0,0,0,0,0,0,1) | 7 | 21 | 35 | 35 | 21 | 7 | |
| 2 | Ректифицированный 6-симплексный ректификованный гептапетон (рил) | (0,0,0,0,0,1,1) | 14 | 63 | 140 | 175 | 105 | 21 | |
| 3 | Усеченный 6-симплексный усеченный гептапетон (тил) | (0,0,0,0,0,1,2) | 14 | 63 | 140 | 175 | 126 | 42 | |
| 4 | Биректифицированный 6-симплексный биректифицированный гептапетон (брил) | (0,0,0,0,1,1,1) | 14 | 84 | 245 | 350 | 210 | 35 | |
| 5 | Сквозной 6-симплексный малый ромбовидный гептапетон (срил) | (0,0,0,0,1,1,2) | 35 | 210 | 560 | 805 | 525 | 105 | |
| 6 | Bitruncated 6-симплексный усеченный гептапетон (батал) | (0,0,0,0,1,2,2) | 14 | 84 | 245 | 385 | 315 | 105 | |
| 7 | Cantitruncated 6-симплекс большой ромбовидный гептапетон (гриль) | (0,0,0,0,1,2,3) | 35 | 210 | 560 | 805 | 630 | 210 | |
| 8 | Ранцинированный 6-симплексный мелкопризматический гептапетон (спил) | (0,0,0,1,1,1,2) | 70 | 455 | 1330 | 1610 | 840 | 140 | |
| 9 | Бикантеллированный 6-симплексный малый биомбированный гептапетон (сабрил) | (0,0,0,1,1,2,2) | 70 | 455 | 1295 | 1610 | 840 | 140 | |
| 10 | Runcitruncated 6-симплекс призматический, усеченный гептапетон (патал) | (0,0,0,1,1,2,3) | 70 | 560 | 1820 | 2800 | 1890 | 420 | |
| 11 | Усеченный 6-симплекс тетрадекапетон (fe) | (0,0,0,1,2,2,2) | 14 | 84 | 280 | 490 | 420 | 140 | |
| 12 | Runcicantellated 6-симплекс призматический гептапетон (прил) | (0,0,0,1,2,2,3) | 70 | 455 | 1295 | 1960 | 1470 | 420 | |
| 13 | Бикантитроусеченный 6-симплекс большой биомбированный гептапетон (габрил) | (0,0,0,1,2,3,3) | 49 | 329 | 980 | 1540 | 1260 | 420 | |
| 14 | Runcicantitruncated 6-симплекс большой призматический гептапетон (гапил) | (0,0,0,1,2,3,4) | 70 | 560 | 1820 | 3010 | 2520 | 840 | |
| 15 | Стерилизованный 6-симплексный мелкоклеточный гептапетон (скальп) | (0,0,1,1,1,1,2) | 105 | 700 | 1470 | 1400 | 630 | 105 | |
| 16 | Бирунцинированный 6-симплекс малый бипризмато-тетрадекапетон (сибпоф) | (0,0,1,1,1,2,2) | 84 | 714 | 2100 | 2520 | 1260 | 210 | |
| 17 | Стеритоусеченный 6-симплекс клетки: усеченный гептапетон (катал) | (0,0,1,1,1,2,3) | 105 | 945 | 2940 | 3780 | 2100 | 420 | |
| 18 | Стерикантеллированный 6-симплекс Cellirhombated гептапетон (крал) | (0,0,1,1,2,2,3) | 105 | 1050 | 3465 | 5040 | 3150 | 630 | |
| 19 | Бирунсусеченный 6-симплекс бипризматический гептапетон (баприл) | (0,0,1,1,2,3,3) | 84 | 714 | 2310 | 3570 | 2520 | 630 | |
| 20 | Стериканитусеченный 6-симплекс клетчатка, хомбированный гептапетон (каграл) | (0,0,1,1,2,3,4) | 105 | 1155 | 4410 | 7140 | 5040 | 1260 | |
| 21 | Стерирунированный 6-симплекс целлипризматический гептапетон (копал) | (0,0,1,2,2,2,3) | 105 | 700 | 1995 | 2660 | 1680 | 420 | |
| 22 | Стерино-усеченный 6-симплексный клеткапризматотрезанный гептапетон (каптал) | (0,0,1,2,2,3,4) | 105 | 945 | 3360 | 5670 | 4410 | 1260 | |
| 23 | Стерируксантеллированный 6-симплексный гуммированный гептапетон (коприл) | (0,0,1,2,3,3,4) | 105 | 1050 | 3675 | 5880 | 4410 | 1260 | |
| 24 | Biruncicantitruncated 6-симплекс большой бипризмато-тетрадекапетон (гибпоф) | (0,0,1,2,3,4,4) | 84 | 714 | 2520 | 4410 | 3780 | 1260 | |
| 25 | Стерильный усеченный 6-симплекс большой клеточный гептапетон (гакал) | (0,0,1,2,3,4,5) | 105 | 1155 | 4620 | 8610 | 7560 | 2520 | |
| 26 | Пятисторонний 6-симплексный малый тери-тетрадекапетон (посох) | (0,1,1,1,1,1,2) | 126 | 434 | 630 | 490 | 210 | 42 | |
| 27 | Пятиусеченный 6-симплекс терацеллированный гептапетон (токал) | (0,1,1,1,1,2,3) | 126 | 826 | 1785 | 1820 | 945 | 210 | |
| 28 | Пятисветвленный 6-симплекс терипризматический гептапетон (топал) | (0,1,1,1,2,2,3) | 126 | 1246 | 3570 | 4340 | 2310 | 420 | |
| 29 | Penticantitruncated 6-симплекс Гептапетон (тограл) | (0,1,1,1,2,3,4) | 126 | 1351 | 4095 | 5390 | 3360 | 840 | |
| 30 | Пятиусеченное усеченное 6-симплексное терицелл, комбинированный гептапетон (токрал) | (0,1,1,2,2,3,4) | 126 | 1491 | 5565 | 8610 | 5670 | 1260 | |
| 31 | Пятизубчатые 6-симплексные терипризматор, гомби-тетрадекапетон (тапорф) | (0,1,1,2,3,3,4) | 126 | 1596 | 5250 | 7560 | 5040 | 1260 | |
| 32 | Пятиусеченный усеченный 6-симплексный теригреатопризматический гептапетон (тагопал) | (0,1,1,2,3,4,5) | 126 | 1701 | 6825 | 11550 | 8820 | 2520 | |
| 33 | Пентистеритусеченный 6-симплекс терицелллитрунки-тетрадекапетон (тактаф) | (0,1,2,2,2,3,4) | 126 | 1176 | 3780 | 5250 | 3360 | 840 | |
| 34 | Пентистерикантитусеченный 6-симплексный терицеллигреаторомбированный гептапетон (такограл) | (0,1,2,2,3,4,5) | 126 | 1596 | 6510 | 11340 | 8820 | 2520 | |
| 35 | Омнитусеченный 6-симплекс великий тери-тетрадекапетон (готаф) | (0,1,2,3,4,5,6) | 126 | 1806 | 8400 | 16800 | 15120 | 5040 | |
B6 семья
Всего существует 63 формы, основанные на всех перестановках Диаграммы Кокстера-Дынкина с одним или несколькими кольцами.
B6 семейство имеет симметрию порядка 46080 (6 факториал х 26).
Они названы Норман Джонсон из операций построения Wythoff над правильным 6-кубом и 6-ортоплексом. Имена Bowers и аббревиатуры даны для перекрестных ссылок.
| # | Диаграмма Кокстера-Дынкина | Символ Шлефли | Имена | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | 0 | ||||
| 36 | т0{3,3,3,3,4} | 6-ортоплекс Hexacontatetrapeton (ну и дела) | 64 | 192 | 240 | 160 | 60 | 12 | |
| 37 | т1{3,3,3,3,4} | Ректифицированный 6-ортоплекс Ректифицированный гексаконатетрапетон (тряпка) | 76 | 576 | 1200 | 1120 | 480 | 60 | |
| 38 | т2{3,3,3,3,4} | Биректифицированный 6-ортоплекс Биректифицированный гексаконатетрапетон (хвастовство) | 76 | 636 | 2160 | 2880 | 1440 | 160 | |
| 39 | т2{4,3,3,3,3} | Биректифицированный 6-куб Двунаправленный гексеракт (брокс) | 76 | 636 | 2080 | 3200 | 1920 | 240 | |
| 40 | т1{4,3,3,3,3} | Ректифицированный 6-куб Исправленный гексеракт (rax) | 76 | 444 | 1120 | 1520 | 960 | 192 | |
| 41 | т0{4,3,3,3,3} | 6-куб Гексеракт (топор) | 12 | 60 | 160 | 240 | 192 | 64 | |
| 42 | т0,1{3,3,3,3,4} | Усеченный 6-ортоплекс Усеченный гексаконатетрапетон (метка) | 76 | 576 | 1200 | 1120 | 540 | 120 | |
| 43 | т0,2{3,3,3,3,4} | Сквозной 6-ортоплекс Гексаконатетрапетон малый ромбовидный (srog) | 136 | 1656 | 5040 | 6400 | 3360 | 480 | |
| 44 | т1,2{3,3,3,3,4} | Усеченный 6-ортоплекс Bitruncated hexacontatetrapeton (ботаг) | 1920 | 480 | |||||
| 45 | т0,3{3,3,3,3,4} | Ранцинированный 6-ортоплекс Гексаконаттрапетон малый призматический (зубчатый) | 7200 | 960 | |||||
| 46 | т1,3{3,3,3,3,4} | Бикантеллированный 6-ортоплекс Гексаконатетрапетон малый биомбированный (сиборг) | 8640 | 1440 | |||||
| 47 | т2,3{4,3,3,3,3} | Треусеченный 6-куб Гексерактигексаконтитетрапетон (xog) | 3360 | 960 | |||||
| 48 | т0,4{3,3,3,3,4} | Стерилизованный 6-ортоплекс Гексаконтатетрапетон малоклеточный (скэг) | 5760 | 960 | |||||
| 49 | т1,4{4,3,3,3,3} | Бирунцинированный 6-куб Малый бипризмато-гексерактигексаконтетрапетон (собпоксог) | 11520 | 1920 | |||||
| 50 | т1,3{4,3,3,3,3} | Двухслойный 6-куб Малый биомбированный гексеракт (саборкс) | 9600 | 1920 | |||||
| 51 | т1,2{4,3,3,3,3} | Обрезанный битом 6-куб Bitruncated hexeract (ботокс) | 2880 | 960 | |||||
| 52 | т0,5{4,3,3,3,3} | Пятиугольный 6-куб Малый тери-гексерактигексаконтитетрапетон (стоксог) | 1920 | 384 | |||||
| 53 | т0,4{4,3,3,3,3} | Стерилизованный 6 кубов Гексеракт малый клетчатый (scox) | 5760 | 960 | |||||
| 54 | т0,3{4,3,3,3,3} | Бегущий 6-куб Малый призматический шестигранник (спокс) | 7680 | 1280 | |||||
| 55 | т0,2{4,3,3,3,3} | Скошенный 6-куб Малый ромбовидный гексеракт (srox) | 4800 | 960 | |||||
| 56 | т0,1{4,3,3,3,3} | Усеченный 6-куб Усеченный гексеракт (tox) | 76 | 444 | 1120 | 1520 | 1152 | 384 | |
| 57 | т0,1,2{3,3,3,3,4} | Усеченный 6-ортоплекс Гексаконатетрапетон большой ромбовидный (грог) | 3840 | 960 | |||||
| 58 | т0,1,3{3,3,3,3,4} | Усеченный 6-ортоплекс Призматоусеченный гексаконатетрапетон (потаг) | 15840 | 2880 | |||||
| 59 | т0,2,3{3,3,3,3,4} | Runcicantellated 6-ортоплекс Гексаконтатрапетон с призматической головкой (прог) | 11520 | 2880 | |||||
| 60 | т1,2,3{3,3,3,3,4} | Бикантитно усеченный 6-ортоплекс Большой биомбированный гексаконатетрапетон (габорг) | 10080 | 2880 | |||||
| 61 | т0,1,4{3,3,3,3,4} | Стеритоусеченный 6-ортоплекс Целлитусеченный гексаконатетрапетон (катог) | 19200 | 3840 | |||||
| 62 | т0,2,4{3,3,3,3,4} | Стерикантеллированный 6-ортоплекс Cellirhombated hexacontatetrapeton (скала) | 28800 | 5760 | |||||
| 63 | т1,2,4{3,3,3,3,4} | Бирунцитусеченный 6-ортоплекс Бипризматоусеченный гексаконатетрапетон (бопракс) | 23040 | 5760 | |||||
| 64 | т0,3,4{3,3,3,3,4} | Стерирунцинированный 6-ортоплекс Целлипризматический гексаконатетрапетон (копог) | 15360 | 3840 | |||||
| 65 | т1,2,4{4,3,3,3,3} | Бирунциркулированный 6-куб Бипризматоусеченный шестигранник (бопраг) | 23040 | 5760 | |||||
| 66 | т1,2,3{4,3,3,3,3} | Двукратноусеченный 6-куб Большой биомбированный гексеракт (габоркс) | 11520 | 3840 | |||||
| 67 | т0,1,5{3,3,3,3,4} | Пятиусеченный 6-ортоплекс Теритусеченный гексаконатетрапетон (такокс) | 8640 | 1920 | |||||
| 68 | т0,2,5{3,3,3,3,4} | Пятисветвленный 6-ортоплекс Terirhombated hexacontatetrapeton (тапокс) | 21120 | 3840 | |||||
| 69 | т0,3,4{4,3,3,3,3} | Стерирунированный 6-куб Целлипризматический гексеракт (копокс) | 15360 | 3840 | |||||
| 70 | т0,2,5{4,3,3,3,3} | Пятиугольник 6-куб Гомбированный гексеракт (топаг) | 21120 | 3840 | |||||
| 71 | т0,2,4{4,3,3,3,3} | Стерикантеллированный 6-куб Cellirhombated hexeract (трещина) | 28800 | 5760 | |||||
| 72 | т0,2,3{4,3,3,3,3} | Runcicantellated 6-куб Призматический гексеракт (прокс) | 13440 | 3840 | |||||
| 73 | т0,1,5{4,3,3,3,3} | Пятиусеченный 6-куб Теритусеченный гексеракт (таког) | 8640 | 1920 | |||||
| 74 | т0,1,4{4,3,3,3,3} | Стеритоусеченный 6-кубик Целочисленный гексеракт (катакс) | 19200 | 3840 | |||||
| 75 | т0,1,3{4,3,3,3,3} | Беги усеченный 6-куб Призматоусеченный шестигранник (потакс) | 17280 | 3840 | |||||
| 76 | т0,1,2{4,3,3,3,3} | Усеченный 6-куб Большой ромбовидный гексеракт (грокс) | 5760 | 1920 | |||||
| 77 | т0,1,2,3{3,3,3,3,4} | Рукоусеченный 6-ортоплекс Большой призматический гексаконатетрапетон (гопог) | 20160 | 5760 | |||||
| 78 | т0,1,2,4{3,3,3,3,4} | Стериканитусеченный 6-ортоплекс Celligreatorhombated hexacontatetrapeton (кагорг) | 46080 | 11520 | |||||
| 79 | т0,1,3,4{3,3,3,3,4} | Стериро-усеченный 6-ортоплекс Celliprismatotruncated hexacontatetrapeton (captog) | 40320 | 11520 | |||||
| 80 | т0,2,3,4{3,3,3,3,4} | Стерируксантеллированный 6-ортоплекс Гексаконтаттрапетон (копраг) | 40320 | 11520 | |||||
| 81 | т1,2,3,4{4,3,3,3,3} | Усеченный 6-куб Грейт бипризмато-гексерактигексаконтетрапетон (гобпоксог) | 34560 | 11520 | |||||
| 82 | т0,1,2,5{3,3,3,3,4} | Пентикоусеченный 6-ортоплекс Terigreatorhombated hexacontatetrapeton (тогриг) | 30720 | 7680 | |||||
| 83 | т0,1,3,5{3,3,3,3,4} | Пятиусеченный 6-ортоплекс Терипризматот усеченный гексаконат трапетон (токракс) | 51840 | 11520 | |||||
| 84 | т0,2,3,5{4,3,3,3,3} | Пятизубчатый 6-куб Терипризматорhombi-hexeractihexacontitetrapeton (типриксог) | 46080 | 11520 | |||||
| 85 | т0,2,3,4{4,3,3,3,3} | Стерируксусный 6-куб Гомбинированный гексеракт (коприкс) | 40320 | 11520 | |||||
| 86 | т0,1,4,5{4,3,3,3,3} | Пентистеритусеченный 6-куб Теричелли-гексерактигексаконтитетрапетон (тактаксог) | 30720 | 7680 | |||||
| 87 | т0,1,3,5{4,3,3,3,3} | Пятизубчатый усеченный 6-куб Терипризматотрезанный шестигранник (токарк) | 51840 | 11520 | |||||
| 88 | т0,1,3,4{4,3,3,3,3} | Стерино-усеченный 6-куб Целлипризматотрезанный шестигранник (каптикс) | 40320 | 11520 | |||||
| 89 | т0,1,2,5{4,3,3,3,3} | Пентикоусеченный 6-куб Теригреат или гомомбированный гексеракт (тогрикс) | 30720 | 7680 | |||||
| 90 | т0,1,2,4{4,3,3,3,3} | Стерикантитроусеченный 6-куб Celligreatorhombated hexeract (кагоркс) | 46080 | 11520 | |||||
| 91 | т0,1,2,3{4,3,3,3,3} | Рукоятокусеченный 6-куб Большой призматический шестигранник (гиппокс) | 23040 | 7680 | |||||
| 92 | т0,1,2,3,4{3,3,3,3,4} | Стерируксусный 6-ортоплекс Большой клетчатый гексаконатетрапетон (гочог) | 69120 | 23040 | |||||
| 93 | т0,1,2,3,5{3,3,3,3,4} | Пятизубец усеченный 6-ортоплекс Теригреатопризматический гексаконтатрапетон (tagpog) | 80640 | 23040 | |||||
| 94 | т0,1,2,4,5{3,3,3,3,4} | Пентистерикантитусеченный 6-ортоплекс Теричеллигреат или гексаконат трапетон (текагорг) | 80640 | 23040 | |||||
| 95 | т0,1,2,4,5{4,3,3,3,3} | Пентистерикантитроусеченный 6-куб Теричеллигреат или гомофобный гексеракт (токагракс) | 80640 | 23040 | |||||
| 96 | т0,1,2,3,5{4,3,3,3,3} | Пентирунцианитусеченный 6-куб Теригреатопризматический гексеракт (tagpox) | 80640 | 23040 | |||||
| 97 | т0,1,2,3,4{4,3,3,3,3} | Усеченный 6-куб Большой клеточный гексеракт (gocax) | 69120 | 23040 | |||||
| 98 | т0,1,2,3,4,5{4,3,3,3,3} | Омниусеченный 6-куб Великий тери-гексерактигексаконтитетрапетон (готаксог) | 138240 | 46080 | |||||
D6 семья
D6 семейство имеет симметрию порядка 23040 (6 факториал х 25).
Это семейство имеет 3 × 16−1 = 47 однородных многогранников Витоффа, созданных пометкой одного или нескольких узлов D6 Диаграмма Кокстера-Дынкина. Из них 31 (2 × 16−1) повторяются из B6 семья и 16 уникальны для этой семьи. Ниже перечислены 16 уникальных форм. Аббревиатуры в стиле Bowers даны для перекрестных ссылок.
| # | Диаграмма Кокстера | Имена | Базовая точка (Альтернативно подписано) | Количество элементов | Circumrad | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 99 | 6-полукуб Хемигексеракт (хакс) | (1,1,1,1,1,1) | 44 | 252 | 640 | 640 | 240 | 32 | 0.8660254 | |
| 100 | Кантик 6-куб Усеченный полугексеракт (thax) | (1,1,3,3,3,3) | 76 | 636 | 2080 | 3200 | 2160 | 480 | 2.1794493 | |
| 101 | Рунический 6-куб Малый ромбовидный полугексеракт (сирхакс) | (1,1,1,3,3,3) | 3840 | 640 | 1.9364916 | |||||
| 102 | Стерический 6-куб Малый призматический полугексеракт (софакс) | (1,1,1,1,3,3) | 3360 | 480 | 1.6583123 | |||||
| 103 | Пентичный 6-куб Малоклеточный полугексеракт (сошакс) | (1,1,1,1,1,3) | 1440 | 192 | 1.3228756 | |||||
| 104 | Runcicantic 6-куб Большой ромбовидный гемигексеракт (гирхакс) | (1,1,3,5,5,5) | 5760 | 1920 | 3.2787192 | |||||
| 105 | Стерикантический 6-куб Призмато-усеченный полугексеракт (питакс) | (1,1,3,3,5,5) | 12960 | 2880 | 2.95804 | |||||
| 106 | Steriruncic 6-кубик Призматический полугексеракт (прохакс) | (1,1,1,3,5,5) | 7680 | 1920 | 2.7838821 | |||||
| 107 | Пентикантический 6-куб Целочисленный полугексеракт (катикс) | (1,1,3,3,3,5) | 9600 | 1920 | 2.5980761 | |||||
| 108 | Пентирункский 6-куб Cellirhombated гемигексеракт (крохакс) | (1,1,1,3,3,5) | 10560 | 1920 | 2.3979158 | |||||
| 109 | Пентистерический 6-куб Целлипризматический полугексеракт (кофикс) | (1,1,1,1,3,5) | 5280 | 960 | 2.1794496 | |||||
| 110 | Стерилункикантический 6-куб Большой призматический полугексеракт (гофакс) | (1,1,3,5,7,7) | 17280 | 5760 | 4.0926762 | |||||
| 111 | Пентируслантический 6-куб Celligreatorhombated гемигексеракт (cagrohax) | (1,1,3,5,5,7) | 20160 | 5760 | 3.7080991 | |||||
| 112 | Пентистерикантический 6-куб Целлипризматотрезанный полугексеракт (каптикс) | (1,1,3,3,5,7) | 23040 | 5760 | 3.4278274 | |||||
| 113 | Pentisteriruncic 6-кубик Гомбинированный гемигексеракт (капрогакс) | (1,1,1,3,5,7) | 15360 | 3840 | 3.2787192 | |||||
| 114 | Pentisteriruncicantic 6-куб Большой клеточный полугексеракт (гочакс) | (1,1,3,5,7,9) | 34560 | 11520 | 4.5552168 | |||||
E6 семья
Существует 39 форм, основанных на всех перестановках Диаграммы Кокстера-Дынкина с одним или несколькими кольцами. Аббревиатуры в стиле Bowers даны для перекрестных ссылок. В E6 семья имеет симметрию порядка 51 840.
| # | Диаграмма Кокстера | Имена | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|
| 5 лиц | 4 лица | Клетки | Лица | Края | Вершины | |||
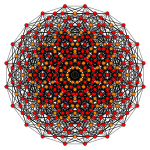
| 115 | 221 Икозигептахептаконтидипетон (як) | 99 | 648 | 1080 | 720 | 216 | 27 | |
| 116 | Ректифицированный 221 Ректифицированный икозигептагептаконтидипетон (роджак) | 126 | 1350 | 4320 | 5040 | 2160 | 216 | |
| 117 | Усеченный 221 Усеченный икозигептагептаконтидипетон (тояк) | 126 | 1350 | 4320 | 5040 | 2376 | 432 | |
| 118 | Собор 221 Икозигептахептаконтидипетон малый ромбовидный (сирджак) | 342 | 3942 | 15120 | 24480 | 15120 | 2160 | |
| 119 | Бегущий 221 Малый демипризматический икосигептагептаконтидипетон (шопжак) | 342 | 4662 | 16200 | 19440 | 8640 | 1080 | |
| 120 | Демифицированный икосигептагептаконтидипетон (хеджак) | 342 | 2430 | 7200 | 7920 | 3240 | 432 | |
| 121 | Bitruncated 221 Усеченный икосигептахептаконтидипетон (ботаджик) | 2160 | ||||||
| 122 | Демиректифицированный икозигептахептаконтидипетон (харджак) | 1080 | ||||||
| 123 | Cantitruncated 221 Икозигептахептаконтидипетон большой ромбовидный (гирджак) | 4320 | ||||||
| 124 | Runcitruncated 221 Демипризматотрезанный икосигептагептаконтидипетон (гопитжак) | 4320 | ||||||
| 125 | Steritruncated 221 Усеченный икозигептагептаконтидипетон (катжак) | 2160 | ||||||
| 126 | Демитусеченный икозигептахептаконтидипетон (хотжак) | 2160 | ||||||
| 127 | Runcicantellated 221 Комбинированный икосигептагептаконтидипетон (хапрояк) | 6480 | ||||||
| 128 | Малый демиромбированный икосигептахептаконтидипетон (шоржак) | 4320 | ||||||
| 129 | Икозигептахептаконтидипетон призматический малый (спояк) | 4320 | ||||||
| 130 | Икозигептахептаконтидипетон (титаяк) усеченный | 4320 | ||||||
| 131 | Runcicantitruncated 221 Великий демипризматический икосигептахептаконтидипетон (гхопжак) | 12960 | ||||||
| 132 | Stericantitruncated 221 Celligreator комбинированный икозигептагептаконтидипетон (cograjik) | 12960 | ||||||
| 133 | Большой демиромбированный икосигептахептаконтидипетон (горжак) | 8640 | ||||||
| 134 | Призмато-усеченный икозигептагептаконтидипетон (потяк) | 12960 | ||||||
| 135 | Демицеллит усеченный икозигептагептаконтидипетон (иктиджик) | 8640 | ||||||
| 136 | Икозигептагептаконтидипетон (прояк) с призмой | 12960 | ||||||
| 137 | Большой призматический икосигептахептаконтидипетон (гапжак) | 25920 | ||||||
| 138 | Демицеллигреат или гомомбированный икосигептагептаконтидипетон (хочгарджик) | 25920 | ||||||
| # | Диаграмма Кокстера | Имена | Количество элементов | |||||
|---|---|---|---|---|---|---|---|---|
| 5 лиц | 4 лица | Клетки | Лица | Края | Вершины | |||
| 139 | 122 Пентаконтатетрапетон (мес.) | 54 | 702 | 2160 | 2160 | 720 | 72 | |
| 140 | Исправленный 122 Ректифицированный пентаконтатетрапетон (баран) | 126 | 1566 | 6480 | 10800 | 6480 | 720 | |
| 141 | Двунаправленный 122 Биректифицированный пентаконтатетрапетон (барм) | 126 | 2286 | 10800 | 19440 | 12960 | 2160 | |
| 142 | Триректифицированный 122 Триректифицированный пентаконтатетрапетон (обрезка) | 558 | 4608 | 8640 | 6480 | 2160 | 270 | |
| 143 | Усеченный 122 Усеченный пентаконтатетрапетон (тим) | 13680 | 1440 | |||||
| 144 | Bitruncated 122 Усеченный пентаконтатетрапетон (битем) | 6480 | ||||||
| 145 | Tritruncated 122 Tritruncated пентаконтатетрапетон (титам) | 8640 | ||||||
| 146 | Квантовый 122 Маленький ромбовидный пентаконтатетрапетон (срам) | 6480 | ||||||
| 147 | Cantitruncated 122 Пентаконтатетрапетон большой ромбовидный (грамм) | 12960 | ||||||
| 148 | Беглый 122 Малый призматический пентаконтатетрапетон (спам) | 2160 | ||||||
| 149 | Двусторонний 122 Малый birhombated pentacontatetrapeton (sabrim) | 6480 | ||||||
| 150 | Двукратно-усеченный 122 Большой birhombated pentacontatetrapeton (gabrim) | 12960 | ||||||
| 151 | Runcitruncated 122 Призмато-усеченный пентаконтатетрапетон (патом) | 12960 | ||||||
| 152 | Runcicantellated 122 Призматический пентаконтат трапетон (пром) | 25920 | ||||||
| 153 | Усеченный 122 Большой призматический пентаконтатетрапетон (гопам) | 51840 | ||||||
Невитхоффовы 6-многогранники
В шести измерениях и выше существует бесконечное количество невыпуклых невитхоффовских однородные многогранники как Декартово произведение из Великая антипризма в 4-х измерениях и правильный многоугольник в 2-х измерениях. Еще не доказано, есть ли больше.
Обычные и однородные соты

Есть четыре основных аффинных Группы Кокстера и 27 призматических групп, которые генерируют регулярные и однородные мозаики в 5-пространственном пространстве:
| # | Группа Кокстера | Диаграмма Кокстера | Формы | |
|---|---|---|---|---|
| 1 | [3[6]] | 12 | ||
| 2 | [4,33,4] | 35 | ||
| 3 | [4,3,31,1] [4,33,4,1+] | 47 (16 новых) | ||
| 4 | [31,1,3,31,1] [1+,4,33,4,1+] | 20 (3 новых) | ||
Обычные и однородные соты включают:
- Всего существует 12 уникальных однородных сот, в том числе:
- Есть 35 однородных сот, в том числе:
- Обычный гиперкубические соты евклидова 5-мерного пространства 5-кубовые соты, с символами {4,33,4},










 =
= 








- Обычный гиперкубические соты евклидова 5-мерного пространства 5-кубовые соты, с символами {4,33,4},
- В наличии 47 однородных сот, 16 новых, в том числе:
- Униформа чередующиеся гиперкубические соты, 5-полукубические соты, с символами h {4,33,4},










 =
= 







 =
= 






- Униформа чередующиеся гиперкубические соты, 5-полукубические соты, с символами h {4,33,4},
- , [31,1,3,31,1]: Есть 20 уникальных перестановок в кольцах и 3 новых. Коксетер называет первую четверть 5 куб. соты, с символами q {4,33,4},






 =
= 









 . Два других новых
. Два других новых 





 =
= 









 ,
, 





 =
= 









 .
.
| # | Группа Кокстера | Диаграмма Кокстера-Дынкина | |
|---|---|---|---|
| 1 | Икс | [3[5],2,∞] | |
| 2 | Икс | [4,3,31,1,2,∞] | |
| 3 | Икс | [4,3,3,4,2,∞] | |
| 4 | Икс | [31,1,1,1,2,∞] | |
| 5 | Икс | [3,4,3,3,2,∞] | |
| 6 | ИксИкс | [4,3,4,2,∞,2,∞] | |
| 7 | ИксИкс | [4,31,1,2,∞,2,∞] | |
| 8 | ИксИкс | [3[4],2,∞,2,∞] | |
| 9 | ИксИксИкс | [4,4,2,∞,2,∞,2,∞] | |
| 10 | ИксИксИкс | [6,3,2,∞,2,∞,2,∞] | |
| 11 | ИксИксИкс | [3[3],2,∞,2,∞,2,∞] | |
| 12 | ИксИксИксИкс | [∞,2,∞,2,∞,2,∞,2,∞] | |
| 13 | ИксИкс | [3[3],2,3[3],2,∞] | |
| 14 | ИксИкс | [3[3],2,4,4,2,∞] | |
| 15 | ИксИкс | [3[3],2,6,3,2,∞] | |
| 16 | ИксИкс | [4,4,2,4,4,2,∞] | |
| 17 | ИксИкс | [4,4,2,6,3,2,∞] | |
| 18 | ИксИкс | [6,3,2,6,3,2,∞] | |
| 19 | Икс | [3[4],2,3[3]] | |
| 20 | Икс | [4,31,1,2,3[3]] | |
| 21 | Икс | [4,3,4,2,3[3]] | |
| 22 | Икс | [3[4],2,4,4] | |
| 23 | Икс | [4,31,1,2,4,4] | |
| 24 | Икс | [4,3,4,2,4,4] | |
| 25 | Икс | [3[4],2,6,3] | |
| 26 | Икс | [4,31,1,2,6,3] | |
| 27 | Икс | [4,3,4,2,6,3] | |
Регулярные и однородные гиперболические соты
Не существует компактных гиперболических групп Кокстера ранга 6, групп, которые могут порождать соты со всеми конечными гранями, и конечных вершина фигуры. Однако есть 12 некомпактных гиперболических групп Кокстера ранга 6, каждая из которых порождает однородные соты в 5-пространстве как перестановки колец диаграмм Кокстера.
= [3,3[5]]: = [(3,3,4,3,3,4)]: | = [4,3,32,1]: | = [3,3,3,4,3]: | = [32,1,1,1]: = [4,3,31,1,1]: |
Замечания о конструкции Витхофа для равномерных 6-многогранников
Конструкция световозвращающей 6-мерной однородные многогранники выполняются через Строительство Wythoff процесс и представлен через Диаграмма Кокстера-Дынкина, где каждый узел представляет собой зеркало. Узлы обведены кружком, чтобы обозначить, какие зеркала активны. Сгенерированный полный набор однородных многогранников основан на уникальных перестановках кольцевых узлов. Равномерные 6-многогранники названы в соответствии с правильные многогранники в каждой семье. У некоторых семейств есть два обычных конструктора, поэтому их можно назвать двумя способами.
Вот основные операторы, доступные для построения и именования однородных 6-многогранников.
Призматические формы и бифуркационные графы могут использовать ту же нотацию индексации усечения, но для ясности требуют явной системы нумерации узлов.
| Операция | Расширенный Символ Шлефли | Кокстер- Дынкин диаграмма | Описание |
|---|---|---|---|
| Родитель | т0{p, q, r, s, t} | Любой правильный 6-многогранник | |
| Исправленный | т1{p, q, r, s, t} | Края полностью обрезаются на отдельные точки. Теперь у 6-многогранника совмещены грани родительского и двойственного. | |
| Двунаправленный | т2{p, q, r, s, t} | Биректификация снижает клетки к их двойники. | |
| Усеченный | т0,1{p, q, r, s, t} | Каждая исходная вершина обрезается, и пробел заполняется новой гранью. Усечение имеет степень свободы, которая имеет одно решение, создающее однородный усеченный 6-многогранник. 6-многогранник имеет свои исходные грани, удвоенные по сторонам, и содержит грани двойственного. | |
| Bitruncated | т1,2{p, q, r, s, t} | Bitrunction преобразует ячейки в их двойное усечение. | |
| Усеченный | т2,3{p, q, r, s, t} | Tritruncation преобразует 4-грани в их двойное усечение. | |
| Собранный | т0,2{p, q, r, s, t} | В дополнение к усечению вершин каждое исходное ребро скошенный на их месте появляются новые прямоугольные грани. Единая песня находится на полпути между родительской и дуальной формами. | |
| Двухслойный | т1,3{p, q, r, s, t} | В дополнение к усечению вершин каждое исходное ребро скошенный на их месте появляются новые прямоугольные грани. Единая песня находится на полпути между родительской и дуальной формами. | |
| Runcinated | т0,3{p, q, r, s, t} | Runcination уменьшает ячейки и создает новые ячейки в вершинах и краях. | |
| Бирунцинированный | т1,4{p, q, r, s, t} | Runcination уменьшает ячейки и создает новые ячейки в вершинах и краях. | |
| Стерилизованный | т0,4{p, q, r, s, t} | Стерилизация уменьшает 4-грани и создает новые 4-грани на вершинах, ребрах и гранях в зазорах. | |
| Пятиугольник | т0,5{p, q, r, s, t} | Pentellation уменьшает 5 граней и создает новые 5 граней в вершинах, ребрах, гранях и ячейках в зазорах. (расширение операция по поводу полипета) | |
| Усеченный | т0,1,2,3,4,5{p, q, r, s, t} | Применяются все пять операторов: усечение, кантелляция, ранцинирование, стерилизация и пентелляция. |
Смотрите также
Примечания
- ^ А предложенное имя полипетон (множественное число: полипета) был защищен от Греческий корень поли- означает "многие", сокращенное пента - означает «пять», и суффикс -на. «Пятерка» относится к размерности 5-многогранника. грани.
- ^ Дитела, многогранники и диады
- ^ Т. Госсет: О регулярных и полурегулярных фигурах в пространстве n измерений, Вестник математики, Macmillan, 1900 г.
- ^ Однородные полипеты и другие шестимерные формы
Рекомендации
- Т. Госсет: О регулярных и полурегулярных фигурах в пространстве n измерений, Посланник математики, Макмиллан, 1900 г.
- А. Буль Стотт: Геометрическое выведение полуправильных из правильных многогранников и заполнения пространств, Верханделинген академии Конинклийке van Wetenschappen, ширина единицы Амстердам, Eerste Sectie 11,1, Амстердам, 1910 г.
- H.S.M. Coxeter:
- H.S.M. Кокстер, М. Longuet-Higgins und J.C.P. Миллер: Однородные многогранники, Философские труды Лондонского королевского общества, Лондон, 1954 г.
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- Клитцинг, Ричард. «6D однородные многогранники (полипеты)».
- Клитцинг, Ричард. «Операторы усечения однородных многогранников».
внешняя ссылка
- Имена многогранников
- Многогранники разной размерности, Джонатан Бауэрс
- Многомерный глоссарий
- Глоссарий по гиперпространству, Георгий Ольшевский.
Фундаментальный выпуклый обычный и однородные соты в размерах 2-9 | ||||||
|---|---|---|---|---|---|---|
| Космос | Семья | / / | ||||
| E2 | Равномерная черепица | {3[3]} | δ3 | hδ3 | qδ3 | Шестиугольный |
| E3 | Равномерно выпуклые соты | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Равномерные 4-соты | {3[5]} | δ5 | hδ5 | qδ5 | 24-ячеечные соты |
| E5 | Равномерные 5-соты | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Равномерные 6-соты | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Равномерные 7-соты | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Равномерные 8-соты | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Равномерные 9-соты | {3[10]} | δ10 | hδ10 | qδ10 | |
| Eп-1 | Униформа (п-1)-соты | {3[n]} | δп | hδп | qδп | 1k2 • 2k1 • k21 |