Измерение - Dimension

| Геометрия | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||
Четыре - / другое измерение | ||||||||||
| Геометры | ||||||||||
по имени | ||||||||||
по периоду
| ||||||||||
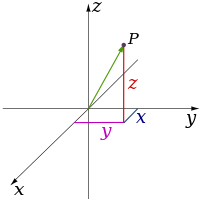
В физика и математика, то измерение из математическое пространство (или объект) неофициально определяется как минимальное количество координаты необходимо указать любые точка внутри.[1][2] Таким образом линия имеет размер, равный единице (1D), потому что для определения точки на нем нужна только одна координата - например, точка 5 на числовой прямой. А поверхность например, самолет или поверхность цилиндр или же сфера имеет измерение двух (2D), потому что для определения точки на нем необходимы две координаты - например, обе широта и долгота требуются, чтобы найти точку на поверхности сферы. Внутри куб, цилиндр или сфера трехмерный (3D), потому что для определения точки в этих пространствах необходимы три координаты.
В классическая механика, Космос и время являются разными категориями и относятся к абсолютное пространство и время. Эта концепция мира - это четырехмерное пространство но не тот, который сочли необходимым описать электромагнетизм. Четыре измерения (4D) пространство-время состоит из События которые не определены абсолютно пространственно и временно, а скорее известны относительно движения наблюдатель. Пространство Минковского приближается к Вселенной без сила тяжести; то псевдоримановы многообразия из общая теория относительности описывать пространство-время с помощью материи и гравитации. 10 размеров используются для описания теория суперструн (6D гиперпространство + 4D), 11 размеров могут описать супергравитация и М-теория (7D гиперпространство + 4D), а пространство состояний квантовая механика является бесконечномерным функциональное пространство.
Концепция измерения не ограничивается физическими объектами. Пространство высокой размерностиs часто встречаются в математике и естественных науках. Они могут быть пространства параметров или же конфигурационные пространства например, в Лагранжиан или же Гамильтонова механика; это абстрактные пробелы, независимо от физического Космос мы живем в.
По математике
В математике размер объекта - это, грубо говоря, количество степени свободы точки, которая движется по этому объекту. Другими словами, размерность - это количество независимых параметры или же координаты которые необходимы для определения положения точки, которая должна находиться на объекте. Например, размер точки равен нулю; размер линия единица, поскольку точка может двигаться по линии только в одном направлении (или в противоположном); размер самолет два и т. д.
Размерность - это внутреннее свойство объекта, в том смысле, что оно не зависит от измерения пространства, в которое объект находится или может быть встроен. Например, изгиб, например круг имеет размер один, потому что положение точки на кривой определяется расстоянием со знаком вдоль кривой до фиксированной точки на кривой. Это не зависит от того факта, что кривую нельзя вложить в Евклидово пространство размерности меньше двух, если это не линия.
Размер Евклидово п-Космос Eпявляется п. Пытаясь обобщить на другие типы пространств, возникает вопрос «что делает Eп п-размерный? "Один из ответов - чтобы покрыть фиксированный мяч в Eп маленькими шарами радиуса ε, нужно порядка ε−п такие маленькие шарики. Это наблюдение приводит к определению Минковского измерение и его более сложный вариант, Хаусдорфово измерение, но есть и другие ответы на этот вопрос. Например, граница шара в Eп выглядит локально как Eп-1 и это приводит к понятию индуктивный размер. Хотя эти понятия согласуются Eп, они оказываются разными, если смотреть на более общие пространства.
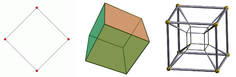
А тессеракт является примером четырехмерного объекта. В то время как за пределами математики термин «измерение» используется так: «Тессеракт имеет четыре измерения", математики обычно выражают это так:" Тессеракт имеет размерность 4", или:" Размер тессеракта является 4 дюйма или: 4D.
Хотя понятие высших измерений восходит к Рене Декарт, существенное развитие многомерной геометрии началось только в 19 веке благодаря работам Артур Кэли, Уильям Роуэн Гамильтон, Людвиг Шлефли и Бернхард Риманн. Римана 1854 г. Хабилитация, 1852 год Шлефли Theorie der vielfachen Kontinuität, и открытие Гамильтоном кватернионы и Джон Т. Грейвс 'открытие октонионы в 1843 г. положил начало геометрии более высоких измерений.
Остальная часть этого раздела исследует некоторые из наиболее важных математических определений размерности.
Векторные пространства
Размерность векторное пространство это количество векторов в любом основа для пробела, то есть количество координат, необходимых для задания любого вектора. Это понятие размерности ( мощность основы) часто называют Измерение Гамеля или же алгебраическая размерность чтобы отличить его от других понятий измерения.
Для не-свободный случае, это обобщает понятие длина модуля.
Коллекторы
Однозначно определенное измерение каждого связаны топологический многообразие можно рассчитать. Связное топологическое многообразие - это локально гомеоморфный к евклидову п-пространство, в котором число п - размерность многообразия.
Для подключенных дифференцируемые многообразия, размер также является измерением касательное векторное пространство в любой момент.
В геометрическая топология, теория многообразий характеризуется относительной элементарностью размерностей 1 и 2, многомерный случаи п > 4 упрощены за счет наличия дополнительного пространства для «работы»; и дела п = 3 и 4 в каком-то смысле самые сложные. Такое положение дел было особенно заметно в различных случаях Гипотеза Пуанкаре, где применяются четыре различных метода доказательства.
Комплексное измерение
Размерность многообразия зависит от базового поля, относительно которого определено евклидово пространство. В то время как анализ обычно предполагает, что коллектор превышает действительные числа, иногда полезно при изучении комплексные многообразия и алгебраические многообразия работать над сложные числа вместо. Комплексное число (Икс + иу) имеет реальная часть Икс и мнимая часть у, где x и y - действительные числа; следовательно, комплексное измерение составляет половину реального измерения.
И наоборот, в алгебраически неограниченных контекстах единственная комплексная система координат может применяться к объекту, имеющему два реальных измерения. Например, обычный двумерный сферическая поверхность, когда задана комплексная метрика, становится Сфера Римана одного сложного измерения.[3]
Разновидности
Размер алгебраическое многообразие могут быть определены различными эквивалентными способами. Вероятно, самый интуитивный способ - это измерение касательное пространство в любом Регулярная точка алгебраического многообразия. Другой интуитивно понятный способ - определить размер как количество гиперплоскости которые необходимы для того, чтобы иметь пересечение с многообразием, которое сводится к конечному числу точек (размерность ноль). Это определение основано на том факте, что пересечение многообразия с гиперплоскостью уменьшает размерность на единицу, если только гиперплоскость не содержит многообразия.
An алгебраический набор будучи конечным объединением алгебраических многообразий, его размерность равна максимуму размерностей его компонентов. Он равен максимальной длине цепочек подмногообразий данного алгебраического множества (длина такой цепочки равна количеству "").
Каждый сорт можно рассматривать как алгебраический стек, и его размерность как разновидность согласуется с размером стека. Однако есть много стопок, которые не соответствуют разновидностям, и некоторые из них имеют отрицательный размер. В частности, если V это разнообразие измерений м и грамм является алгебраическая группа измерения п действующий на V, то стек частных [V/грамм] имеет измерение м − п.[4]
Измерение Крулля
В Измерение Крулля из коммутативное кольцо - максимальная длина цепочек главные идеалы в нем цепочка длиной п являясь последовательностью простых идеалов, связанных включением. Оно сильно связано с размерностью алгебраического многообразия из-за естественного соответствия между подмногообразиями и простыми идеалами кольца многочленов на многообразии.
Для алгебра над полем, размерность как векторное пространство конечно тогда и только тогда, когда его размерность Крулля равна 0.
Топологические пространства
Для любого нормальное топологическое пространство Икс, то Размер покрытия Лебега из Икс определяется как наименьший целое число п для которого справедливо: любое открытая крышка имеет открытое уточнение (вторая открытая крышка, где каждый элемент является подмножеством элемента в первой обложке), так что ни одна точка не включается более чем в п + 1 элементы. В этом случае тусклый Икс = п. За Икс многообразие, это совпадает с указанной выше размерностью. Если такого целого нет п существует, то размерность Икс называется бесконечным, и пишут тусклый Икс = ∞. Более того, Икс имеет размерность −1, т.е. dim Икс = −1 если и только если Икс пусто. Это определение покрывающей размерности может быть расширено с класса нормальных пространств на все Тихоновские пространства просто заменив в определении термин «открытый» на термин «функционально открытый".
An индуктивный размер можно определить индуктивно следующее. Рассмотрим дискретный набор точек (например, конечный набор точек) быть 0-мерными. Перетаскивая 0-мерный объект в каком-либо направлении, можно получить одномерный объект. Перетаскивая одномерный объект в новое направление, получается двумерный объект. В общем случае получается (п + 1) -мерный объект путем перетаскивания п-мерный объект в новый направление. Индуктивная размерность топологического пространства может относиться к малый индуктивный размер или большой индуктивный размер, и основан на аналогии, что в случае метрических пространств (п + 1) -мерный шары есть п-размерный границы, позволяя индуктивное определение, основанное на размерности границ открытых множеств. Более того, граница дискретного набора точек - это пустое множество, и поэтому можно считать, что пустое множество имеет размерность -1.[5]
Аналогично для класса Комплексы CW, размер объекта самый большой п для чего п-скелет нетривиально. Интуитивно это можно описать так: если исходное пространство можно непрерывно деформированный в коллекцию многомерные треугольники соединенные своими гранями со сложной поверхностью, то размер объекта равен размеру этих треугольников.[нужна цитата ]
Хаусдорфово измерение
В Хаусдорфово измерение полезен для изучения структурно сложных множеств, особенно фракталы. Размерность Хаусдорфа определена для всех метрические пространства и, в отличие от размеров, рассмотренных выше, также может иметь нецелые действительные значения.[6] В размер коробки или же Минковского измерение это вариант той же идеи. В общем, существует больше определений фрактальные измерения которые работают для очень нерегулярных множеств и достигают нецелочисленных положительных вещественных значений. Было обнаружено, что фракталы полезны для описания многих природных объектов и явлений.[7][страница нужна ][8][страница нужна ]
Гильбертовы пространства
Каждый Гильбертово пространство признает ортонормированный базис, и любые две такие базы для определенного пространства имеют одинаковые мощность. Эта мощность называется размерностью гильбертова пространства. Это измерение конечно тогда и только тогда, когда пространство Измерение Гамеля конечно, и в этом случае два измерения совпадают.
В физике
Пространственные размеры
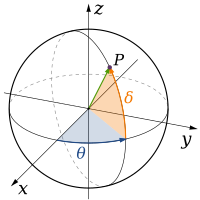
Теории классической физики описывают три физические размеры: из определенной точки в Космос, основные направления, в которых мы можем двигаться, - это вверх / вниз, влево / вправо и вперед / назад. Движение в любом другом направлении можно выразить в терминах этих трех. Движение вниз - то же самое, что движение вверх на отрицательное расстояние. Движение по диагонали вверх и вперед - это то же самое, что и название направления; т.е., двигаясь в линейная комбинация вверх и вперед. В простейшей форме: линия описывает одно измерение, плоскость описывает два измерения, а куб описывает три измерения. (Видеть Космос и Декартова система координат.)
Количество размеры | Примеры систем координат | |||
|---|---|---|---|---|
| 1 |
| |||
| 2 |
| |||
| 3 |
|
Время
А временное измерение, или же измерение времени, это измерение времени. Время часто называют "четвертое измерение "по этой причине, но это не означает, что это пространственное измерение. Временное измерение - это один из способов измерения физических изменений. Оно воспринимается иначе, чем три пространственных измерения, поскольку существует только одно из них, и что мы не может свободно перемещаться во времени, но субъективно двигаться в одном направлении.
Уравнения, используемые в физике для моделирования реальности, не трактуют время так, как его обычно воспринимают люди. Уравнения классическая механика находятся симметричный по времени, а уравнения квантовой механики обычно симметричны, если и время, и другие величины (например, обвинять и паритет ) перевернуты. В этих моделях восприятие времени, текущего в одном направлении, является артефактом законы термодинамики (мы воспринимаем время как текущее в направлении увеличения энтропия ).
Самая известная трактовка времени как измерения: Пуанкаре и Эйнштейн с специальная теория относительности (и продлен до общая теория относительности ), который рассматривает воспринимаемое пространство и время как компоненты четырехмерного многообразие, известный как пространство-время, а в частном, плоском - как Пространство Минковского.
Дополнительные размеры
В физике общепринятой нормой являются три измерения пространства и одно временное. Однако есть теории, которые пытаются объединить четыре фундаментальные силы путем введения дополнительные размеры /гиперпространство. В частности, теория суперструн требует 10 измерений пространства-времени, и происходит от более фундаментальной 11-мерной теории, предварительно названной М-теория который включает пять ранее отличавшихся теорий суперструн. Теория супергравитации также продвигает 11D пространство-время = 7D гиперпространство + 4 общих измерения. На сегодняшний день нет прямых экспериментальных или наблюдательных данных, подтверждающих существование этих дополнительных измерений. Если гиперпространство существует, оно должно быть скрыто от нас каким-то физическим механизмом. Одна хорошо изученная возможность состоит в том, что дополнительные измерения могут быть «свернуты» в таких крошечных масштабах, что будут фактически невидимы для текущих экспериментов. Ограничения на размер и другие свойства дополнительных измерений устанавливаются экспериментами с частицами.[требуется разъяснение ] например, в Большой адронный коллайдер.[9]
В 1921 г. Теория Калуцы-Клейна представлены 5D, включая дополнительное измерение пространства. На уровне квантовая теория поля, Теория Калуцы – Клейна объединяет сила тяжести с измерять взаимодействия, основанные на осознании того, что гравитация, распространяющаяся в небольших, компактных дополнительных измерениях, эквивалентна калибровочным взаимодействиям на больших расстояниях. В частности, когда геометрия дополнительных измерений тривиальна, она воспроизводит электромагнетизм. Однако при достаточно высоких энергиях или коротких расстояниях эта установка по-прежнему страдает теми же патологиями, которые, как известно, препятствуют прямым попыткам описать квантовая гравитация. Поэтому для этих моделей по-прежнему требуется УФ завершение того типа, который предназначена предоставить теория струн. В частности, теория суперструн требует шести компактных измерений (6D гиперпространство), образующих Многообразие Калаби – Яу. Таким образом, теорию Калуцы-Клейна можно рассматривать либо как неполное описание само по себе, либо как подмножество построения модели теории струн.
В дополнение к маленьким и свернутым дополнительным измерениям могут быть дополнительные измерения, которые вместо этого не очевидны, потому что материя, связанная с нашей видимой Вселенной, локализована на (3 + 1) -мерный подпространство. Таким образом, дополнительные размеры не обязательно должны быть маленькими и компактными, но могут быть большие дополнительные размеры. D-браны представляют собой динамические протяженные объекты различной размерности, предсказанные теорией струн, которые могут играть эту роль. Они обладают тем свойством, что возбуждения открытой струны, связанные с калибровочными взаимодействиями, ограничены брана их конечными точками, в то время как замкнутые струны, которые опосредуют гравитационное взаимодействие, могут свободно распространяться во все пространство-время или «балку». Это может быть связано с тем, почему гравитация экспоненциально слабее, чем другие силы, поскольку она эффективно растворяется, когда распространяется в объем более высокого измерения.
Некоторые аспекты физики браны были применены к космология. Например, космология газа на бране[10][11] пытается объяснить, почему существует три измерения пространства, используя топологические и термодинамические соображения. Согласно этой идее, это было бы потому, что три - это наибольшее количество пространственных измерений, где струны могут пересекаться. Если изначально существует много витков струн вокруг компактных размеров, пространство может расшириться до макроскопических размеров только после того, как эти обмотки будут устранены, что требует, чтобы струны противоположно намотаны, чтобы найти друг друга и аннигилировать. Но струны могут найти друг друга только для того, чтобы аннигилировать со значимой скоростью в трех измерениях, поэтому следует, что только три измерения пространства могут увеличиваться в размерах при такой начальной конфигурации.
Дополнительные размеры называются универсальный если все поля могут одинаково свободно распространяться внутри них.
В компьютерной графике и пространственных данных
Несколько типов цифровых систем основаны на хранении, анализе и визуализации геометрических фигур, в том числе программное обеспечение для иллюстраций, Системы автоматизированного проектирования, и Географические информационные системы. В различных векторных системах используется широкий спектр структур данных для представления фигур, но почти все они в основном основаны на наборе геометрические примитивы соответствующие пространственным размерам: [12]
- Точка (0-мерный), единственная координата в Декартова система координат.
- Линия или же Ломаная линия (1-мерный), обычно представленный в виде упорядоченного списка точек, взятых из непрерывной линии, после чего ожидается, что программное обеспечение интерполировать промежуточная форма линии в виде прямых или изогнутых отрезков.
- Многоугольник (2-мерный), обычно представляемый в виде линии, которая замыкается в своих конечных точках, представляя границу двухмерной области. Ожидается, что программное обеспечение будет использовать эту границу для разделения двухмерного пространства на внутреннее и внешнее.
- Поверхность (3-мерный), представленный с использованием различных стратегий, таких как многогранник состоящий из соединенных граней многоугольника. Ожидается, что программное обеспечение будет использовать эту поверхность для разделения трехмерного пространства на внутреннее и внешнее.
Часто в этих системах, особенно в ГИС и Картография, представление явлений реального мира может иметь другое (обычно более низкое) измерение, чем представляемое явление. Например, город (двухмерный регион) может быть представлен как точка, или дорога (трехмерный объем материала) может быть представлена как линия. Этот размерное обобщение коррелирует с тенденциями в пространственном познании. Например, вопрос о расстоянии между двумя городами предполагает концептуальную модель городов в виде точек, а указание направлений, включающих движение «вверх», «вниз» или «вдоль» дороги, подразумевает одномерную концептуальную модель. Это часто делается в целях эффективности данных, визуальной простоты или когнитивной эффективности и приемлемо, если различие между представлением и представленным понятно, но может вызвать путаницу, если пользователи информации предполагают, что цифровая форма является идеальным представлением реальности. (т.е. веря, что дороги на самом деле являются линиями).
Сети и измерение
Некоторые сложные сети характеризуются фрактальные измерения.[13] Концепция измерения может быть обобщена на сети, встроенные в пространство.[14] Размерность характеризует их пространственные ограничения.
В литературе
Научная фантастика в текстах часто упоминается понятие «измерение», когда речь идет о параллельные или альтернативные вселенные или другое воображаемое планы существования. Это использование происходит из идеи, что для путешествия в параллельные / альтернативные вселенные / планы существования нужно путешествовать в направлении / измерении помимо стандартных. Фактически, другие вселенные / планы находятся на небольшом расстоянии от нашей, но это расстояние находится в четвертом (или более высоком) пространственном (или непространственном) измерении, а не в стандартных.
Одна из самых известных научно-фантастических историй об истинной геометрической размерности, которую часто рекомендуют в качестве отправной точки для тех, кто только начинает исследовать такие вопросы, - это повесть 1884 года. Плоская земля Эдвин А. Эбботт. Исаак Азимов в своем предисловии к изданию Signet Classics 1984 г. Плоская земля как «Лучшее введение в способ восприятия измерений».
Идея других измерений была включена во многие ранние научно-фантастические рассказы, которые, например, занимали видное место в Майлз Дж. Брейер с Аппендикс и очки (1928) и Мюррей Ленстер с Катапульта пятого измерения (1931); и нерегулярно появлялся в научной фантастике к 1940-м годам. Классические истории с участием других измерений включают Роберт А. Хайнлайн с - И он построил кривой дом (1941), в котором калифорнийский архитектор проектирует дом на основе трехмерной проекции тессеракта; и Алан Э. Норс с Тигр за хвост и Вселенная между (оба 1951 г.). Еще одна ссылка Мадлен Л'Энгль роман Морщинка во времени (1962), который использует пятое измерение как способ «тессерации Вселенной» или «складывания» пространства для быстрого перемещения по нему. Четвертое и пятое измерения также являются ключевым компонентом книги. Мальчик, который полностью изменился к Уильям Слейтор.
В философии
Иммануил Кант в 1783 г. писал: «Всюду пространство (которое само не является границей другого пространства) имеет три измерения и что пространство в целом не может иметь больше измерений, основано на предположении, что не более трех линий могут пересекаться под прямым углом в один момент. Это утверждение вообще невозможно показать из понятий, оно непосредственно опирается на интуицию и даже на чистую интуицию. априори потому что это аподиктически (очевидно) определенно ".[15]
«Пространство имеет четыре измерения» - это рассказ, опубликованный в 1846 году немецким философом и экспериментальный психолог Густав Фехнер под псевдоним «Доктор Мизес». Главный герой сказки - тень, которая знает о других тенях и способна общаться с ними, но застряла на двухмерной поверхности. Согласно Фехнеру, этот «человек-тень» воспринимает третье измерение как измерение времени.[16] История очень похожа на "Аллегория пещеры "представлены в Платон с Республика (c. 380 г. до н.э.).
Саймон Ньюкомб написал статью для Бюллетень Американского математического общества в 1898 году под названием «Философия гиперпространства».[17] Линда Дэлримпл Хендерсон придумал термин «философия гиперпространства», используемый для описания письма, которое использует более высокие измерения для исследования метафизический Темы в своей диссертации 1983 года о четвертом измерении в искусстве начала двадцатого века.[18] Примеры «философов гиперпространства» включают Чарльз Ховард Хинтон, первый писатель в 1888 году, употребивший слово «тессеракт»;[19] и русский эзотерик Успенский П. Д..
Больше размеров
| Геометрия | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||
Четыре - / другое измерение | ||||||||||
| Геометры | ||||||||||
по имени | ||||||||||
по периоду
| ||||||||||
Смотрите также
Темы по параметрам
- Нуль
- Один
- Два
- Три
- Четыре
- Высшие измерения
- Бесконечный
Рекомендации
Эта статья нужны дополнительные цитаты для проверка. (Май 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- ^ "Любопытно об астрономии". Curious.astro.cornell.edu. Архивировано из оригинал на 2014-01-11. Получено 2014-03-03.
- ^ "MathWorld: Dimension". Mathworld.wolfram.com. 2014-02-27. В архиве из оригинала от 25.03.2014. Получено 2014-03-03.
- ^ Яу, Шинг-Тунг; Надис, Стив (2010). «4. Слишком хорошо, чтобы быть правдой». Форма внутреннего пространства: теория струн и геометрия скрытых измерений Вселенной. Основные книги. С. 60–. ISBN 978-0-465-02266-3.
- ^ Фантечи, Барбара (2001), «Стеки для всех» (PDF), Европейский математический конгресс, том I, Прогр. Математика, 201, Birkhäuser, стр. 349–359, в архиве (PDF) из оригинала 17.01.2006
- ^ Гуревич, Витольд; Уоллман, Генри (2015). Теория измерений (ПМС-4), Том 4. Princeton University Press. п. 24. ISBN 978-1-4008-7566-5. Выдержка страницы 24
- ^ Фрактальное измерение В архиве 2006-10-27 на Wayback Machine, Факультет математики и статистики Бостонского университета
- ^ Бунде, Армин; Хавлин, Шломо, ред. (2012) [1991]. Фракталы и неупорядоченные системы (2-е изд.). Springer. ISBN 978-3-642-84868-1.
- ^ Бунде, Армин; Хавлин, Шломо, ред. (2013) [1994]. "1. Краткое введение в фрактальную геометрию 1.2.1 Кривая Коха". Фракталы в науке. Springer. С. 3–. ISBN 978-3-642-77953-4.
- ^ CMS Collaboration (2011). «Поиск микроскопических сигнатур черных дыр на Большом адронном коллайдере». Phys. Lett. B. 697 (5): 434–453. arXiv:1012.3375. Bibcode:2011ФЛБ..697..434С. Дои:10.1016 / j.physletb.2011.02.032. S2CID 118488193. CMS-EXO-10-017, CERN-PH-EP-2010-073.
- ^ Brandenberger, R .; Вафа, К. (1989). «Суперструны в ранней вселенной». Ядерная физика B. 316 (2): 391–410. Bibcode:1989НуФБ.316..391Б. Дои:10.1016/0550-3213(89)90037-0.
- ^ Скотт Уотсон, Космология бранного газа В архиве 2014-10-27 на Wayback Machine (pdf).
- ^ Векторные модели данных, Основы географических информационных систем, Saylor Academy, 2012 г.
- ^ Песня, Хаоминг; Хавлин, Шломо; Максе, Эрнан А. (2005). «Самоподобие сложных сетей». Природа. 433 (7024): 392–395. arXiv:cond-mat / 0503078v1. Bibcode:2005Натура.433..392С. Дои:10.1038 / природа03248. PMID 15674285. S2CID 1985935.
- ^ Дацин, Ли; Космидис, Космас; Бунде, Армин; Хавлин, Шломо (2011). «Измерение пространственно встроенных сетей» (PDF). Природа Физика. 7 (6): 481. Bibcode:2011НатФ ... 7..481Д. Дои:10.1038 / nphys1932.
- ^ Пролегомены, § 12
- ^ Банчофф, Томас Ф. (1990). «От плоской земли к гиперграфике: взаимодействие с более высокими измерениями». Междисциплинарные научные обзоры. 15 (4): 364. Дои:10.1179/030801890789797239. В архиве из оригинала 2013-04-14.
- ^ Ньюкомб, Саймон (1898). «Философия гиперпространства». Бюллетень Американского математического общества. 4 (5): 187. Дои:10.1090 / S0002-9904-1898-00478-0.
- ^ Крюгер, Рунетт (2007). «Искусство в четвертом измерении: придание формы форме - абстрактные картины Пита Мондриана» (PDF). Пространства утопии: электронный журнал (5): 11. В архиве (PDF) из оригинала от 29.09.2011.
- ^ Пиковер, Клиффорд А. (2009), «Тессеракт», Книга по математике: от Пифагора до 57-го измерения, 250 вех в истории математики, Sterling Publishing, стр. 282, г. ISBN 978-1-4027-5796-9, в архиве из оригинала от 30.03.2017.
дальнейшее чтение
- Мурти, Катта Г. (2014). «1. Системы одновременных линейных уравнений» (PDF). Вычислительная и алгоритмическая линейная алгебра и n-мерная геометрия. Мировое научное издательство. Дои:10.1142/8261. ISBN 978-981-4366-62-5.
- Эбботт, Эдвин А. (1884). Флатландия: Многогранный романс. Лондон: Seely & Co.
- —. Плоская земля: ... Проект Гутенберг.
- —; Стюарт, Ян (2008). Аннотированная равнина: многомерный роман. Основные книги. ISBN 978-0-7867-2183-2.
- Банчофф, Томас Ф. (1996). За пределами третьего измерения: геометрия, компьютерная графика и высшие измерения. Научная американская библиотека. ISBN 978-0-7167-6015-3.
- Пиковер, Клиффорд А. (2001). Серфинг в гиперпространстве: понимание высших вселенных за шесть простых уроков. Oxford University Press. ISBN 978-0-19-992381-6.
- Ракер, Руди (2014) [1984]. Четвертое измерение: к геометрии высшей реальности. Курьерская корпорация. ISBN 978-0-486-77978-2. Предварительный просмотр Google
- Каку, Мичио (1994). Гиперпространство, научная одиссея в 10-м измерении. Издательство Оксфордского университета. ISBN 978-0-19-286189-4.
- Краусс, Лоуренс М. (2005). Скрываясь в зеркале. Викинг Пресс. ISBN 978-0-670-03395-9.
внешняя ссылка
- Коупленд, Эд (2009). «Дополнительные измерения». Шестьдесят символов. Брэди Харан для Ноттингемский университет.