Векторное пространство - Vector space

Не путать с Векторное поле.

Эта статья о линейных (векторных) пространствах. Для структуры в геометрии падения см. Линейное пространство (геометрия). Для компании, занимающейся космическими технологиями, см. Векторные космические системы.

Сложение векторов и скалярное умножение: вектор v (синий) добавляется к другому вектору ш (красный, верхний рисунок). Ниже, ш растягивается в 2 раза, что дает сумму v + 2ш.

А векторное пространство (также называемый линейное пространство) представляет собой набор объектов, называемых векторов, который может быть добавлен вместе и умноженный («масштабируется») по номерам, называется скаляры. Скаляры часто считаются действительные числа, но есть также векторные пространства со скалярным умножением на сложные числа, рациональное число, или вообще любой поле. Операции сложения векторов и скалярного умножения должны удовлетворять определенным требованиям, которые называются векторными. аксиомы (перечислены ниже в § Определение ). Чтобы указать, что скаляры являются действительными или комплексными числами, термины реальное векторное пространство и комплексное векторное пространство часто используются.

Определенные наборы Евклидовы векторы являются общими примерами векторного пространства. Они представляют физический такие количества, как силы, где любые две силы (одного типа) могут быть добавлены, чтобы получить третье, а умножение вектор силы реальным множителем является другой вектор силы. В том же духе (но более геометрический смысл), векторы, представляющие перемещения в плоскости или трехмерное пространство также образуют векторные пространства. Векторы в векторных пространствах не обязательно должны быть объектами в виде стрелок, как они представлены в упомянутых примерах: векторы считаются абстрактными. математические объекты с особыми свойствами, которые в некоторых случаях можно представить в виде стрелок.

Векторные пространства являются предметом линейная алгебра и хорошо характеризуются своими измерение, который, грубо говоря, определяет количество независимых направлений в пространстве. Бесконечномерные векторные пространства естественным образом возникают в математический анализ в качестве функциональные пространства, векторами которого являются функции. Эти векторные пространства обычно наделены некоторой дополнительной структурой, такой как топология, что позволяет рассматривать вопросы близости и непрерывность. Среди этих топологий те, которые определены норма или же внутренний продукт чаще используются (снабжены понятием расстояние между двумя векторами). Это особенно касается Банаховы пространства и Гильбертовы пространства, которые являются фундаментальными в математическом анализе.

Исторически первые идеи, ведущие к векторным пространствам, можно проследить еще в 17 веке. аналитическая геометрия, матрицы, системы линейные уравнения и евклидовы векторы. Современная, более абстрактная трактовка, впервые сформулированная Джузеппе Пеано в 1888 г. охватывает более общие объекты, чем Евклидово пространство, но большую часть теории можно рассматривать как расширение классических геометрических идей, таких как линии, самолеты и их многомерные аналоги.

Сегодня векторные пространства применяются повсюду. математика, наука и инженерное дело. Это подходящее линейно-алгебраическое понятие для работы с системы линейных уравнений. Они предлагают основу для Разложение Фурье, который используется в сжатие изображений процедуры, и они обеспечивают среду, которая может использоваться для методов решения для уравнения в частных производных. Кроме того, векторные пространства представляют собой абстрактное, безкоординатный способ работы с геометрическими и физическими объектами, такими как тензоры. Это, в свою очередь, позволяет исследовать местные свойства коллекторы методами линеаризации. Векторные пространства можно обобщить несколькими способами, что приведет к более продвинутым понятиям в геометрии и абстрактная алгебра.

Введение и определение

Понятие векторного пространства сначала будет объяснено путем описания двух конкретных примеров:

Первый пример: стрелки в плоскости

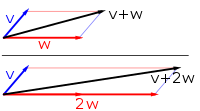
Первый пример векторного пространства состоит из стрелки в фиксированном самолет, начиная с одной фиксированной точки. Это используется в физике для описания силы или же скорости. Учитывая любые две такие стрелки, v и ш, то параллелограмм Между этими двумя стрелками есть одна диагональная стрелка, которая также начинается в начале координат. Эта новая стрелка называется сумма двух стрелок и обозначается v + ш.^[1] В частном случае двух стрелок на одной строке их сумма равна стрелке на этой строке, длина которой равна сумме или разнице длин, в зависимости от того, имеют ли стрелки одинаковое направление. Еще одна операция, которую можно выполнить с помощью стрелок, - это масштабирование: при любом положительном настоящий номер а, стрелка, имеющая то же направление, что и v, но его длина увеличивается или уменьшается за счет умножения его длины на а, называется умножение из v к а. Обозначается аv. Когда а отрицательный, аv вместо этого определяется как стрелка, указывающая в противоположном направлении.

Ниже показано несколько примеров: если а = 2, результирующий вектор аш имеет то же направление, что и ш, но растягивается до удвоенной длины ш (правое изображение ниже). Эквивалентно, 2ш это сумма ш + ш. Более того, (−1)v = −v имеет противоположное направление и такую ​​же длину, как v (синий вектор направлен вниз на правом изображении).

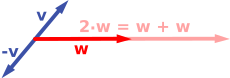Второй пример: упорядоченные пары чисел

Второй ключевой пример векторного пространства - пары действительных чисел. Икс и у. (Порядок компонентов Икс и у имеет значение, поэтому такую ​​пару также называют упорядоченная пара.) Такая пара записывается как (Икс, у). Сумма двух таких пар и умножение пары на число определяется следующим образом:

${\displaystyle (x_{1},y_{1})+(x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2})}$

и

${\displaystyle a(x,y)=(ax,ay)}$ .

Первый приведенный выше пример сводится к этому, если стрелки представлены парой Декартовы координаты их конечных точек.

Определение

В этой статье векторы выделены жирным шрифтом, чтобы отличать их от скаляров.^{[nb 1]}

Векторное пространство над поле F это набор  V вместе с двумя операциями, которые удовлетворяют восьми аксиомам, перечисленным ниже. В следующих, V × V обозначает Декартово произведение из V с собой, и → обозначает отображение от одного набора к другому.

• Первая операция под названием векторное сложение или просто добавление + : V × V → V, принимает любые два вектораv и ш и присваивает им третий вектор, который обычно записывается как v + ш, и назвал сумму этих двух векторов. (Результирующий вектор также является элементом множества V.)
• Вторая операция, называемая скалярное умножение · : F × V → V， Принимает любой скаляра и любой векторv и дает другой вектораv. (Аналогично вектор аv является элементом множества V. Скалярное умножение не следует путать с скалярное произведение, также называемый внутренний продукт или же скалярное произведение, который является дополнительной структурой, присутствующей в некоторых конкретных, но не во всех векторных пространствах. Скалярное умножение - это умножение вектора к скаляр; другой - умножение двух векторов производство скаляр.)

Элементы V обычно называют векторов. ЭлементыF обычно называют скаляры. Общие символы для обозначения векторных пространств включают ${\displaystyle U}$, ${\displaystyle V}$ и ${\displaystyle W}$.^[1]

В двух приведенных выше примерах поле - это поле действительных чисел, а набор векторов состоит из плоских стрелок с фиксированной начальной точкой и пар действительных чисел соответственно.

Чтобы квалифицировать как векторное пространство, наборV а операции сложения и умножения должны соответствовать ряду требований, называемых аксиомы.^[2] Они перечислены в таблице ниже, где ты, v и ш обозначим произвольные векторы из V, и а и б обозначим скаляры в F.^[3][4]

Аксиома	Смысл
Ассоциативность сложения	ты + (v + ш) = (ты + v) + ш
Коммутативность сложения	ты + v = v + ты
Элемент идентичности сложения	Существует элемент 0 ∈ V, называется нулевой вектор, так что v + 0 = v для всех v ∈ V.
Обратные элементы сложения	Для каждого v ∈ V, существует элемент −v ∈ V, называется Противоположное число из v, так что v + (−v) = 0.
Совместимость скалярного умножения с умножением полей	а(бv) = (ab)v [nb 2]
Элемент идентичности скалярного умножения	1v = v, куда 1 обозначает мультипликативная идентичность в F.
Распределительность скалярного умножения относительно сложения векторов	а(ты + v) = аты + аv
Дистрибутивность скалярного умножения по сложению полей	(а + б)v = аv + бv

Эти аксиомы обобщают свойства векторов, представленных в приведенных выше примерах. Действительно, результат сложения двух упорядоченных пар (как во втором примере выше) не зависит от порядка слагаемых:

(Икс_v, у_v) + (Икс_ш, у_ш) = (Икс_ш, у_ш) + (Икс_v, у_v).

Аналогично, в геометрическом примере векторов как стрелок, v + ш = ш + v поскольку параллелограмм, определяющий сумму векторов, не зависит от порядка векторов. Все остальные аксиомы можно проверить аналогичным образом в обоих примерах. Таким образом, игнорируя конкретную природу конкретного типа векторов, определение включает эти два и многие другие примеры в одно понятие векторного пространства.

Вычитание двух векторов и деление на (ненулевой) скаляр можно определить как

${\displaystyle {\begin{aligned}\mathbf {v} -\mathbf {w} &=\mathbf {v} +(-\mathbf {w} )\\{\frac {\mathbf {v} }{a}}&={\frac {1}{a}}\mathbf {v} \end{aligned}}}$.

Когда скалярное поле F это действительные числа р, векторное пространство называется реальное векторное пространство. Когда скалярное поле является сложные числа C, векторное пространство называется комплексное векторное пространство. Эти два случая чаще всего используются в инженерии. Общее определение векторного пространства позволяет скалярам быть элементами любого фиксированного поле F. Это понятие тогда известно как F-векторное пространство или векторное пространство над F. Поле - это, по сути, набор чисел, обладающих добавление, вычитание, умножение и разделение операции.^{[№ 3]} Например, рациональное число сформировать поле.

В отличие от интуиции, проистекающей из векторов в плоских и многомерных случаях, в общих векторных пространствах нет понятия близость, углы или же расстояния. Чтобы иметь дело с такими вопросами, вводятся определенные типы векторных пространств; видеть § Векторные пространства с дополнительной структурой ниже, чтобы узнать больше.

Альтернативные формулировки и элементарные следствия

Сложение векторов и скалярное умножение - это операции, удовлетворяющие закрытие свойство: ты + v и аv находятся в V для всех а в F, и ты, v в V. В некоторых более старых источниках эти свойства упоминаются как отдельные аксиомы.^[5]

Говоря языком абстрактная алгебра, первые четыре аксиомы эквивалентны требованию, чтобы набор векторов был абелева группа под дополнением. Остальные аксиомы придают этой группе F-модуль структура. Другими словами, есть гомоморфизм колец ж с поля F в кольцо эндоморфизмов группы векторов. Тогда скалярное умножение аv определяется как (ж(а))(v).^[6]

Есть ряд прямых следствий аксиом векторного пространства. Некоторые из них происходят от элементарная теория групп, применительно к аддитивной группе векторов: например, нулевой вектор 0 из V и аддитивная обратная −v любого вектора v уникальны. Дальнейшие свойства следуют с использованием также закона распределения для скалярного умножения, например аv равно 0 если и только если а равно 0 или же v равно 0.

История

Дальнейшая информация: История алгебры

Векторные пространства происходят из аффинная геометрия, путем введения координаты в плоском или трехмерном пространстве. Около 1636 г. французские математики Рене Декарт и Пьер де Ферма основанный аналитическая геометрия путем отождествления решений уравнения двух переменных с точками на плоскости изгиб.^[7] Чтобы получить геометрические решения без использования координат, Больцано ввел в 1804 г. определенные операции с точками, линиями и плоскостями, которые являются предшественниками векторов.^[8] Эта работа была использована в концепции барицентрические координаты к Мебиус в 1827 г.^[9] Основа определения векторов была Беллавит 'понятие двойной точки, ориентированного сегмента, один из концов которого является началом, а другой - целью. Векторы были пересмотрены с представлением сложные числа к Арганд и Гамильтон и начало кватернионы последним.^[10] Они элементы в р² и р⁴; лечить их с помощью линейные комбинации возвращается к Laguerre в 1867 г., который также определил системы линейных уравнений.

В 1857 г. Кэли представил матричная запись что позволяет гармонизировать и упростить линейные карты. Примерно в то же время Грассманн изучал барицентрическое исчисление, начатое Мёбиусом. Он представлял себе наборы абстрактных объектов, наделенных операциями.^[11] В его творчестве концепции линейная независимость и измерение, а также скалярные произведения присутствуют. На самом деле работа Грассмана 1844 года выходит за рамки векторных пространств, поскольку его рассмотрение умножения также привело его к тому, что сегодня называют алгебры. Итальянский математик Пеано был первым, кто дал современное определение векторных пространств и линейных отображений в 1888 году.^[12]

Важное развитие векторных пространств связано с построением функциональные пространства к Анри Лебег. Позднее это было формализовано Банах и Гильберта, около 1920 г.^[13] В это время, алгебра и новое поле функциональный анализ начали взаимодействовать, особенно с ключевыми концепциями, такими как пространства п-интегрируемые функции и Гильбертовы пространства.^[14] Также в это время были выполнены первые исследования, касающиеся бесконечномерных векторных пространств.

Примеры

Основная статья: Примеры векторных пространств

Координатное пространство

Простейший пример векторного пространства над полем F это само поле, снабженное его стандартным сложением и умножением. В общем, все п- пары (последовательности длины п)

(а₁, а₂, ..., а_п)

элементов F образуют векторное пространство, которое обычно обозначают F^п и назвал координатное пространство.^[15] Дело п = 1 - упомянутый выше простейший пример, в котором поле F также рассматривается как векторное пространство над собой. Дело F = р и п = 2 обсуждалось во введении выше.

Комплексные числа и другие расширения полей

Набор сложные числа C, то есть числа, которые можно записать в виде Икс + иу за действительные числа Икс и у куда я это мнимая единица, сформируем векторное пространство над вещественными числами обычным сложением и умножением: (Икс + иу) + (а + ib) = (Икс + а) + я(у + б) и c ⋅ (Икс + иу) = (c ⋅ Икс) + я(c ⋅ у) для реальных чисел Икс, у, а, б и c. Различные аксиомы векторного пространства вытекают из того факта, что одни и те же правила выполняются для арифметики комплексных чисел.

На самом деле пример комплексных чисел по сути тот же (то есть изоморфный) в векторное пространство упорядоченных пар действительных чисел, упомянутых выше: если мы думаем о комплексном числе Икс + я у как представление упорядоченной пары (Икс, у) в комплексная плоскость тогда мы видим, что правила сложения и скалярного умножения точно соответствуют правилам из предыдущего примера.

В более общем смысле, расширения полей предоставить другой класс примеров векторных пространств, особенно в алгебре и алгебраическая теория чисел: поле F содержащий меньшее поле E является E-векторном пространстве, заданными операциями умножения и сложения F.^[16] Например, комплексные числа представляют собой векторное пространство над р, а расширение поля ${\displaystyle \mathbf {Q} (i{\sqrt {5}})}$ это векторное пространство над Q.

Функциональные пространства

Основная статья: Функциональное пространство

Сложение функций: сумма синуса и экспоненциальной функции равна ${\displaystyle \sin +\exp :\mathbb {R} \to \mathbb {R} }$ с ${\displaystyle (\sin +\exp )(x)=\sin(x)+\exp(x)}$

Функции из любого фиксированного набора Ω в поле F также формируют векторные пространства, выполняя точечное сложение и скалярное умножение. То есть сумма двух функций ж и грамм это функция (ж + грамм) данный

(ж + грамм)(ш) = ж(ш) + грамм(ш),

и то же самое для умножения. Такие функциональные пространства встречаются во многих геометрических ситуациях, когда Ω это реальная линия или интервал, или другой подмножества из р. Многие понятия в топологии и анализе, такие как непрерывность, интегрируемость или же дифференцируемость хорошо себя ведут в отношении линейности: суммы и скалярные кратные функции, обладающие таким свойством, все еще обладают этим свойством.^[17] Следовательно, набор таких функций - векторные пространства. Более подробно они изучаются с помощью методов функциональный анализ, видеть ниже.^{[требуется разъяснение ]} Алгебраические ограничения также дают векторные пространства: векторное пространство F[Икс] дан кем-то полиномиальные функции:

ж(Икс) = р₀ + р₁Икс + ... + р_п−1Икс^п−1 + р_пИкс^п, где коэффициенты р₀, ..., р_п находятся в F.^[18]

Линейные уравнения

Основные статьи: Линейное уравнение, Линейное дифференциальное уравнение, и Системы линейных уравнений

Системы однородные линейные уравнения тесно связаны с векторными пространствами.^[19] Например, решения

а	+	3б	+	c	= 0
4а	+	2б	+	2c	= 0

задаются троек с произвольными а, б = а/2, и c = −5а/2. Они образуют векторное пространство: суммы и скалярные кратные таких троек по-прежнему удовлетворяют тем же отношениям трех переменных; таким образом, они тоже являются решениями. Матрицы может использоваться для сжатия нескольких линейных уравнений, как указано выше, в одно векторное уравнение, а именно

АИкс = 0,

куда А = ${\displaystyle {\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}}$ - матрица, содержащая коэффициенты данных уравнений, Икс это вектор (а, б, c), АИкс обозначает матричный продукт, и 0 = (0, 0) - нулевой вектор. Аналогичным образом, растворы однородных линейные дифференциальные уравнения образуют векторные пространства. Например,

ж′′(Икс) + 2ж′(Икс) + ж(Икс) = 0

дает ж(Икс) = а е^−Икс + bx e^−Икс, куда а и б - произвольные постоянные, а е^Икс это естественная экспоненциальная функция.

Основа и размер

Основные статьи: Основа и Измерение

Вектор v в р² (синий) выражено по разным основаниям: с использованием стандартная основа из р² v = Иксе₁ + уе₂ (черный), и используя другой, неортогональный основа: v = ж₁ + ж₂ (красный).

Базы позволяют представлять векторы последовательность скаляров называется координаты или же составные части. Базис - это (конечное или бесконечное) множество B = {б_я}_{я ∈ я} векторов б_я, для удобства часто индексируется некоторыми набор индексов я, который охватывает все пространство и является линейно независимый. «Охват всего пространства» означает, что любой вектор v можно выразить в виде конечной суммы (называемой линейная комбинация ) базовых элементов:

${\displaystyle \mathbf {v} =a_{1}\mathbf {b} _{i_{1}}+a_{2}\mathbf {b} _{i_{2}}+\cdots +a_{n}\mathbf {b} _{i_{n}},}$

(1)

где а_k являются скалярами, называемыми координатами (или компонентами) вектора v относительно основы B, и б_яk (k = 1, ..., п) элементы B. Линейная независимость означает, что координаты а_k однозначно определены для любого вектора в векторном пространстве.

Например, векторы координат е₁ = (1, 0, ..., 0), е₂ = (0, 1, 0, ..., 0), к е_п = (0, 0, ..., 0, 1), составляют основу F^п, называется стандартная основа, поскольку любой вектор (Икс₁, Икс₂, ..., Икс_п) можно однозначно выразить как линейную комбинацию этих векторов:

(Икс₁, Икс₂, ..., Икс_п) = Икс₁(1, 0, ..., 0) + Икс₂(0, 1, 0, ..., 0) + ... + Икс_п(0, ..., 0, 1) = Икс₁е₁ + Икс₂е₂ + ... + Икс_пе_п.

Соответствующие координаты Икс₁, Икс₂, ..., Икс_п просто Декартовы координаты вектора.

Каждое векторное пространство имеет основу. Это следует из Лемма Цорна, эквивалентная формулировка Аксиома выбора.^[20] Учитывая другие аксиомы Теория множеств Цермело – Френкеля, существование базисов равносильно выбранной аксиоме.^[21] В лемма об ультрафильтрации, которая слабее выбранной аксиомы, означает, что все базы данного векторного пространства имеют одинаковое количество элементов, или мощность (ср. Теорема размерности для векторных пространств ).^[22] Это называется измерение векторного пространства, обозначаемого dim V. Если пространство натянуто на конечное число векторов, приведенные выше утверждения могут быть доказаны без такого фундаментального вклада теории множеств.^[23]

Размерность координатного пространства F^п является п, на основании выставленного выше. Размерность кольца многочленов F[Икс] представил над^{[требуется разъяснение ]} является счетно бесконечный, основу составляет 1, Икс, Икс², ... А тем более, размерность более общих функциональных пространств, таких как пространство функций на некотором (ограниченном или неограниченном) интервале, бесконечна.^{[№ 4]} При подходящих предположениях регулярности используемых коэффициентов размерность пространства решений однородной обыкновенное дифференциальное уравнение равна степени уравнения.^[24] Например, пространство решений для уравнение выше^{[требуется разъяснение ]} генерируется е^−Икс и xe^−Икс. Эти две функции линейно независимы над р, поэтому размерность этого пространства равна двум, как и степень уравнения.

Расширение поля над рациональными числами Q можно рассматривать как векторное пространство над Q (путем определения сложения векторов как сложения полей, определения скалярного умножения как умножения полей на элементы Q, и в противном случае игнорируя умножение поля). Размер (или степень ) расширения поля Q(α) над Q зависит от α. Если α удовлетворяет некоторому полиномиальному уравнению

$${\displaystyle q_{n}\alpha ^{n}+q_{n-1}\alpha ^{n-1}+\cdots +q_{0}=0}$$

с рациональными коэффициентами q_п, ..., q₀ (другими словами, если α равно алгебраический ) размерность конечна. Точнее, он равен степени минимальный многочлен имея α как корень.^[25] Например, комплексные числа C представляют собой двумерное вещественное векторное пространство, порожденное 1 и мнимая единица я. Последний удовлетворяет я² + 1 = 0, уравнение второй степени. Таким образом, C является двумерным р-векторное пространство (и, как любое поле, одномерное, как векторное пространство над собой, C). Если α не алгебраический, размерность Q(α) над Q бесконечно. Например, при α = π такого уравнения нет, другими словами, π есть трансцендентный.^[26]

Линейные карты и матрицы

Основная статья: Линейная карта

Связь двух векторных пространств может быть выражена как линейная карта или же линейное преобразование. Они есть функции которые отражают структуру векторного пространства, то есть сохраняют суммы и скалярное умножение:

${\displaystyle f(\mathbf {v} +\mathbf {w} )=f(\mathbf {v} )+f(\mathbf {w} )}$ и ж(а · v) ${\displaystyle =}$ а · ж(v) для всех v и ш в V, все а в F.^[27]

An изоморфизм линейная карта ж : V → W такой, что существует обратная карта грамм : W → V, которая представляет собой карту, в которой два возможных композиции ж ∘ грамм : W → W и грамм ∘ ж : V → V находятся карты идентичности. Эквивалентно, ж оба взаимно однозначны (инъективный ) и на (сюръективный ).^[28] Если существует изоморфизм между V и W, два пространства называются изоморфный; тогда они по существу идентичны векторным пространствам, поскольку все тождества, выполняемые в V через ж, перевезены в аналогичные в W, и наоборот через грамм.

Описание вектора стрелки v по его координатам Икс и у дает изоморфизм векторных пространств.

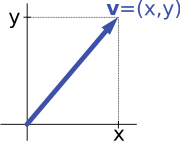
Например, векторные пространства «стрелки на плоскости» и «упорядоченные пары чисел» во введении изоморфны: плоская стрелка v отбытие в источник некоторых (фиксированных) система координат можно выразить как упорядоченную пару, учитывая Икс- и у-компонент стрелки, как показано на изображении справа. И наоборот, учитывая пару (Икс, у), стрелка проходит мимо Икс вправо (или влево, если Икс отрицательно), и у вверх (вниз, если у отрицательно) поворачивает стрелку назад v.

Линейные карты V → W между двумя векторными пространствами образуют векторное пространство Hom_F(V, W), также обозначается L (V, W).^[29] Пространство линейных отображений из V к F называется двойное векторное пространство, обозначенный V^∗.^[30] Через инъективное естественный карта V → V^∗∗, любое векторное пространство можно вложить в его двуручный; отображение является изоморфизмом тогда и только тогда, когда пространство конечномерно.^[31]

Когда-то основа V выбрано, линейные отображения ж : V → W полностью определяются заданием образов базисных векторов, поскольку любой элемент V выражается однозначно как их линейная комбинация.^[32] Если тусклый V = тусклый W, а Индивидуальная переписка между фиксированными базами V и W приводит к линейному отображению, которое отображает любой базисный элемент V к соответствующему базисному элементу W. Это изоморфизм по самому своему определению.^[33] Следовательно, два векторных пространства изоморфны, если их размерности совпадают, и наоборот. Другой способ выразить это - любое векторное пространство полностью засекречен (вплоть до изоморфизм) по размерности, одно число. В частности, любые п-размерный F-векторное пространство V изоморфен F^п. Однако не существует «канонического» или предпочтительного изоморфизма; на самом деле изоморфизм φ : F^п → V равносильно выбору базиса V, отображая стандартный базис F^п к V, через φ. Свобода выбора удобной основы особенно полезна в бесконечномерном контексте; видеть ниже.^{[требуется разъяснение ]}

Матрицы

Основные статьи: Матрица и Детерминант

Типовая матрица

Матрицы полезное понятие для кодирования линейных карт.^[34] Они записаны в виде прямоугольного массива скаляров, как на изображении справа. Любой м-к-п матрица А дает линейную карту из F^п к F^м, следующими

${\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\ldots ,\sum _{j=1}^{n}a_{mj}x_{j}\right)}$, куда ${\displaystyle \sum }$ обозначает суммирование,

или, используя матричное умножение матрицы А с координатным вектором Икс:

Икс ↦ АИкс.

Более того, после выбора баз V и W, любой линейная карта ж : V → W однозначно представлен матрицей через это присваивание.^[35]

Объем этого параллелепипед является абсолютным значением определителя матрицы 3 на 3, образованной векторами р₁, р₂, и р₃.

В детерминант det (А) из квадратная матрица А является скаляром, который сообщает, является ли связанное отображение изоморфизмом: для этого достаточно и необходимо, чтобы определитель был ненулевым.^[36] Линейное преобразование р^п соответствует реальному п-к-п матрица сохранение ориентации тогда и только тогда, когда его определитель положителен.

Собственные значения и собственные векторы

Основная статья: Собственные значения и собственные векторы

Эндоморфизмы, линейные карты ж : V → V, особенно важны, поскольку в этом случае векторы v можно сравнить с их изображением под ж, ж(v). Любой ненулевой вектор v удовлетворение λv = ж(v), куда λ является скаляром, называется собственный вектор из ж с собственное значение λ.^{[№ 5][37]} Эквивалентно, v является элементом ядро разницы ж − λ · Идентификатор (где Id - карта идентичности V → V). Если V конечномерно, это можно перефразировать с помощью определителей: ж имеющий собственное значение λ эквивалентно

det (ж − λ · Id) = 0.

Изложив определение определителя, можно увидеть, что выражение в левой части является полиномиальной функцией от λ, называется характеристический многочлен из ж.^[38] Если поле F достаточно велик, чтобы содержать ноль этого многочлена (что автоматически происходит при F алгебраически замкнутый, Такие как F = C) любое линейное отображение имеет хотя бы один собственный вектор. Векторное пространство V может иметь или не обладать собственный базис, базис, состоящий из собственных векторов. Это явление регулируется Иорданская каноническая форма карты.^{[39][№ 6]} Набор всех собственных векторов, соответствующих конкретному собственному значению ж образует векторное пространство, известное как собственное подпространство соответствующему собственному значению (и ж) обсуждаемый. Для достижения спектральная теорема, соответствующее утверждение в бесконечномерном случае, необходим аппарат функционального анализа, см. ниже.^{[требуется разъяснение ]}

Основные конструкции

В дополнение к приведенным выше конкретным примерам существует ряд стандартных линейных алгебраических конструкций, которые дают векторные пространства, связанные с заданными. В дополнение к определениям, данным ниже, они также характеризуются универсальные свойства, которые определяют объект Икс указав линейные карты из Икс в любое другое векторное пространство.

Подпространства и факторпространства

Основные статьи: Линейное подпространство и Факторное векторное пространство

Линия, проходящая через источник (синий, толстый) в р³ - линейное подпространство. Это пересечение двух самолеты (зеленый и желтый).

Непустой подмножество W векторного пространства V который замкнут относительно сложения и скалярного умножения (и поэтому содержит 0-вектор V) называется линейное подпространство из V, или просто подпространство из V, когда окружающее пространство однозначно является векторным пространством.^{[40][№ 7]} Подпространства V являются векторными пространствами (над одним и тем же полем) сами по себе. Пересечение всех подпространств, содержащих данное множество S векторов называется его охватывать, и это наименьшее подпространство в V содержащий набор S. В терминах элементов промежуток - это подпространство, состоящее из всех линейные комбинации элементов S.^[41]

Линейное подпространство размерности 1 - это векторная линия. Линейное подпространство размерности 2 - это вектор самолет. Линейное подпространство, которое содержит все элементы, кроме одного из базиса объемлющего пространства, является векторная гиперплоскость. В векторном пространстве конечной размерности п, векторная гиперплоскость, таким образом, является подпространством размерности п – 1.

Аналог подпространств факторно-векторные пространства.^[42] Для любого подпространства W ⊂ V, фактор-пространство V/W ("V по модулю W") определяется следующим образом: как набор, он состоит из v + W = {v + ш : ш ∈ W}, куда v - произвольный вектор из V. Сумма двух таких элементов v₁ + W и v₂ + W является (v₁ + v₂) + W, а скалярное умножение дается выражением а · (v + W) = (а · v) + W. Ключевым моментом в этом определении является то, что v₁ + W = v₂ + W если и только если разница v₁ и v₂ лежит в W.^{[№ 8]} Таким образом, фактор-пространство «забывает» информацию, содержащуюся в подпространстве W.

В ядро кер (ж) линейного отображения ж : V → W состоит из векторов v которые сопоставлены с 0 в W.^[43] Ядро и изображение я(ж) = {ж(v) : v ∈ V} являются подпространствами V и W, соответственно.^[44] Существование ядер и образов является частью утверждения, что категория векторных пространств (над фиксированным полем F) является абелева категория, то есть корпус математических объектов и сохраняющих структуру отображений между ними ( категория ), который ведет себя так же, как категория абелевых групп.^[45] Из-за этого многие заявления, такие как первая теорема об изоморфизме (также называемый теорема ранга-недействительности в терминах матрицы)

V / кер (ж) ≡ im (ж).

а вторая и третья теоремы об изоморфизме могут быть сформулированы и доказаны способом, очень похожим на соответствующие утверждения для группы.

Важный пример - ядро ​​линейного отображения Икс ↦ АИкс для некоторой фиксированной матрицы А, так как над.^{[требуется разъяснение ]} Ядром этого отображения является подпространство векторов Икс такой, что АИкс = 0, что и есть множество решений системы однородных линейных уравнений, принадлежащих А. Это понятие распространяется также на линейные дифференциальные уравнения

${\displaystyle a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0}$, где коэффициенты а_я функции в Икс, тоже.

На соответствующей карте

${\displaystyle f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}}}$,

то производные функции ж появляются линейно (в отличие от ж′′(Икс)², Например). Поскольку дифференцирование - линейная процедура (т. Е. (ж + грамм)′ = ж′ + грамм ′ и (c·ж)′ = c·ж′ для постоянного c) это назначение является линейным и называется линейный дифференциальный оператор. В частности, решения дифференциального уравнения D(ж) = 0 образуют векторное пространство (над р или же C).

Прямой продукт и прямая сумма

Основные статьи: Прямой продукт и Прямая сумма модулей

В прямой продукт векторных пространств и прямая сумма векторных пространств - это два способа объединения индексированного семейства векторных пространств в новое векторное пространство.

В прямой продукт ${\displaystyle \textstyle {\prod _{i\in I}V_{i}}}$ семейства векторных пространств V_я состоит из множества всех кортежей (v_я)_{я ∈ я}, которые указывают для каждого индекса я в некоторых набор индексов я элемент v_я из V_я.^[46] Сложение и скалярное умножение выполняется покомпонентно. Вариантом этой конструкции является прямая сумма ${\displaystyle \oplus _{i\in I}V_{i}}$ (также называемый сопродукт и обозначен ${\displaystyle \textstyle {\coprod _{i\in I}V_{i}}}$), где разрешены только наборы с конечным числом ненулевых векторов. Если индекс установлен я конечно, две конструкции согласуются, но в целом они разные.

Тензорное произведение

Основная статья: Тензорное произведение векторных пространств

В тензорное произведение V ⊗_F W, или просто V ⊗ W, двух векторных пространств V и W одно из центральных понятий полилинейная алгебра который имеет дело с расширением таких понятий, как линейные отображения до нескольких переменных. Карта грамм : V × W → Икс называется билинейный если грамм линейна по обеим переменным v и ш. То есть для фиксированного ш карта v ↦ грамм(v, ш) линейна в указанном выше смысле и аналогично при фиксированном v.

Тензорное произведение - это особое векторное пространство, которое является универсальный получатель билинейных карт грамм, следующее. Оно определяется как векторное пространство, состоящее из конечных (формальных) сумм символов, называемых тензоры

v₁ ⊗ ш₁ + v₂ ⊗ ш₂ + ... + v_п ⊗ ш_п,

в соответствии с правилами

а · (v ⊗ ш) = (а · v) ⊗ ш = v ⊗ (а · ш), куда а скаляр,

(v₁ + v₂) ⊗ ш = v₁ ⊗ ш + v₂ ⊗ ш, и

v ⊗ (ш₁ + ш₂) = v ⊗ ш₁ + v ⊗ ш₂.^[47]

Коммутативная диаграмма изображающий универсальное свойство тензорного произведения.

Эти правила гарантируют, что карта ж от V × W к V ⊗ W что отображает кортеж (v, ш) к v ⊗ ш билинейный. Универсальность утверждает, что данный любой векторное пространство Икс и любой билинейная карта грамм : V × W → Икс, существует уникальная карта ты, показанный на схеме пунктирной стрелкой, сочинение с ж равно грамм: ты(v ⊗ ш) = грамм(v, ш).^[48] Это называется универсальная собственность тензорного произведения, экземпляра метода, широко используемого в продвинутой абстрактной алгебре, для косвенного определения объектов путем указания карт из этого объекта или в этот объект.

Векторные пространства с дополнительной структурой

С точки зрения линейной алгебры, векторные пространства полностью понятны, поскольку любое векторное пространство с точностью до изоморфизма характеризуется своей размерностью. Однако векторные пространства как таковой не предлагают рамок для решения вопроса, который имеет решающее значение для анализа, является ли последовательность функций сходится к другой функции. Точно так же линейная алгебра не приспособлена для работы с бесконечная серия, поскольку операция сложения позволяет добавить только конечное число членов. Следовательно, потребности функциональный анализ требуют рассмотрения дополнительных конструкций.

Векторное пространство может быть задано частичный заказ ≤, при котором можно сравнивать некоторые векторы.^[49] Например, п-мерное реальное пространство р^п можно упорядочить, сравнивая его векторы покомпонентно. Упорядоченные векторные пространства, Например Пространства Рисса, имеют фундаментальное значение для Интеграция Лебега, который основан на способности выразить функцию как разность двух положительных функций

ж = ж⁺ − ж⁻,

куда ж⁺ обозначает положительную часть ж и ж⁻ отрицательная часть.^[50]

Нормированные векторные пространства и внутренние пространства продукта

Основные статьи: Нормированное векторное пространство и Внутреннее пространство продукта

«Измерительные» векторы выполняются указанием норма, датум, который измеряет длины векторов, или внутренний продукт, который измеряет углы между векторами. Обозначены нормы и внутренние продукты ${\displaystyle |\mathbf {v} |}$ и ${\displaystyle \langle \mathbf {v} ,\mathbf {w} \rangle }$, соответственно. Из данных внутреннего продукта следует, что длины векторов также могут быть определены путем определения связанной нормы. ${\displaystyle |\mathbf {v} |:={\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}}$. Векторные пространства, наделенные такими данными, известны как нормированные векторные пространства и внутренние пространства продукта, соответственно.^[51]

Координатное пространство F^п может быть укомплектован стандартным скалярное произведение:

${\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle =\mathbf {x} \cdot \mathbf {y} =x_{1}y_{1}+\cdots +x_{n}y_{n}.}$

В р², это отражает общее понятие угла между двумя векторами Икс и у, посредством закон косинусов:

${\displaystyle \mathbf {x} \cdot \mathbf {y} =\cos \left(\angle (\mathbf {x} ,\mathbf {y} )\right)\cdot |\mathbf {x} |\cdot |\mathbf {y} |.}$

Из-за этого два вектора, удовлетворяющие ${\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle =0}$ называются ортогональный. Важный вариант стандартного скалярного произведения используется в Пространство Минковского: р⁴ наделен произведением Лоренца

${\displaystyle \langle \mathbf {x} |\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}.}$^[52]

В отличие от стандартного скалярного произведения, это не положительно определенный: ${\displaystyle \langle \mathbf {x} |\mathbf {x} \rangle }$ также принимает отрицательные значения, например для ${\displaystyle \mathbf {x} =(0,0,0,1)}$. Выделяя четвертую координату -соответствует времени, в отличие от трех пространственных измерений - делает его полезным для математической обработки специальная теория относительности.

Топологические векторные пространства

Основная статья: Топологическое векторное пространство

Вопросы сходимости рассматриваются путем рассмотрения векторных пространств. V неся совместимый топология, структура, позволяющая говорить об элементах близко друг к другу.^[53][54] Совместимость здесь означает, что сложение и скалярное умножение должны быть непрерывные карты. Грубо говоря, если Икс и у в V, и а в F варьироваться на ограниченную величину, то также Икс + у и аИкс.^{[№ 9]} Чтобы иметь смысл указывать величину изменения скаляра, поле F также должен нести топологию в этом контексте; обычно выбирают действительные или комплексные числа.

В таком топологические векторные пространства можно рассмотреть серии векторов. В бесконечная сумма

${\displaystyle \sum _{i=0}^{\infty }f_{i}}$

обозначает предел соответствующих конечных частичных сумм последовательности (ж_я)_я∈N элементов V. Например, ж_я могут быть (действительными или сложными) функциями, принадлежащими некоторым функциональное пространство V, и в этом случае серия функциональная серия. В режим конвергенции ряда зависит от топологии, наложенной на функциональное пространство. В таких случаях, поточечная сходимость и равномерное схождение два ярких примера.

Единица "сферы" в р² состоят из плоских векторов нормы 1. Изображены единичные сферы в различных п-нормы, за п = 1, 2 и ∞. Ромб большего размера обозначает баллы с нормой 1, равной 2.

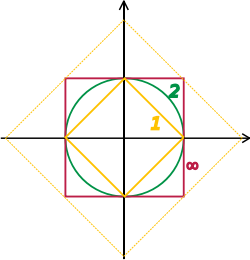
Чтобы убедиться в существовании пределов некоторой бесконечной серии, нужно ограничить внимание пространствами, в которых Последовательность Коши имеет предел; такое векторное пространство называется полный. Грубо говоря, векторное пространство является полным при условии, что оно содержит все необходимые ограничения. Например, векторное пространство многочленов на единичном интервале [0,1], снабженное топология равномерной сходимости не является полной, потому что любую непрерывную функцию на [0,1] можно равномерно аппроксимировать последовательностью многочленов, Аппроксимационная теорема Вейерштрасса.^[55] Напротив, пространство все непрерывные функции на [0,1] с той же топологией полны.^[56] Норма порождает топологию, определяя, что последовательность векторов v_п сходится к v если и только если

${\displaystyle {\text{lim}}_{n\rightarrow \infty }|\mathbf {v} _{n}-\mathbf {v} |=0.}$

Банаховы и гильбертовы пространства - это полные топологические векторные пространства, топологии которых задаются, соответственно, нормой и внутренним произведением. Их исследование - ключевая часть функциональный анализ - фокусируется на бесконечномерных векторных пространствах, поскольку все нормы конечномерных топологических векторных пространств порождают одно и то же понятие сходимости.^[57] Изображение справа показывает эквивалентность 1-нормы и ∞-нормы на р²: поскольку единичные «шары» охватывают друг друга, последовательность сходится к нулю в одной норме тогда и только тогда, когда это происходит в другой норме. В бесконечномерном случае, однако, обычно будут неэквивалентные топологии, что делает изучение топологических векторных пространств более богатым, чем изучение векторных пространств без дополнительных данных.

С концептуальной точки зрения все понятия, относящиеся к топологическим векторным пространствам, должны соответствовать топологии. Например, вместо того, чтобы рассматривать все линейные карты (также называемые функционалы ) V → W, отображения между топологическими векторными пространствами должны быть непрерывными.^[58] В частности, (топологическое) двойственное пространство V^∗ состоит из непрерывных функционалов V → р (или чтобы C). Фундаментальный Теорема Хана – Банаха занимается разделением подпространств подходящих топологических векторных пространств непрерывными функционалами.^[59]

Банаховы пространства

Основная статья: Банахово пространство

Банаховы пространства, представлен Стефан Банах, являются полными нормированными векторными пространствами.^[60]

Первый пример: векторное пространство ${\displaystyle \ell ^{p}}$ состоящий из бесконечных векторов с действительными элементами ${\displaystyle \mathbf {x} =\left(x_{1},x_{2},\ldots ,x_{n},\ldots \right)}$чей ${\displaystyle p}$-норма ${\displaystyle (1\leq {p}\leq \infty )}$данный

${\displaystyle \left\Vert \mathbf {x} \right\Vert _{p}:=\left(\sum _{i}\left\vert x_{i}\right\vert ^{p}\right)^{\frac {1}{p}}}$ за ${\displaystyle p<\infty }$ и ${\displaystyle \left\Vert \mathbf {x} \right\Vert _{\infty }:={\text{sup}}_{i}\left\vert x_{i}\right\vert }$.

Топологии бесконечномерного пространства ${\displaystyle \ell ^{p}}$ неэквивалентны для разных ${\displaystyle p}$. Например, последовательность векторов ${\displaystyle \mathbf {x} _{n}=\left(2^{-n},2^{-n},\ldots ,2^{-n},0,0,\ldots \right)}$, в котором первый ${\displaystyle 2^{n}}$ компоненты ${\displaystyle 2^{-n}}$ и следующие ${\displaystyle 0}$, сходится к нулевой вектор за ${\displaystyle p=\infty }$, но не для ${\displaystyle p=1}$:

${\displaystyle \left\Vert \mathbf {x} _{n}\right\Vert _{_{\infty }}=\sup(2^{-n},0)=2^{-n}\rightarrow 0}$, но ${\displaystyle \left\Vert \mathbf {x} _{n}\right\Vert _{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1.}$

В более общем смысле, чем последовательности действительных чисел, функции ${\displaystyle f\colon \Omega \to \mathbb {R} }$наделены нормой, заменяющей указанную выше сумму на Интеграл Лебега

${\displaystyle \left\Vert {f}\right\Vert _{p}:=\left(\int _{\Omega }\left\vert {f}\left(x\right)\right\vert ^{p}\,{d\mu \left(x\right)}\right)^{\frac {1}{p}}.}$

Пространство интегрируемые функции на данном домен ${\displaystyle \Omega }$ (например, интервал), удовлетворяющий ${\displaystyle \left\Vert {f}\right\Vert _{p}<\infty }$, и снабженные этой нормой называются Пространства Лебега, обозначенный ${\displaystyle L^{\;\!p}\left(\Omega \right)}$.^{[№ 10]}

Эти пространства полные.^[61] (Если использовать Интеграл Римана вместо этого пространство нет полная, что можно рассматривать как оправдание теории интеграции Лебега.^{[№ 11]}) Конкретно это означает, что для любой последовательности интегрируемых по Лебегу функций ${\displaystyle f_{1},f_{2},\ldots ,f_{n},\ldots }$ с${\displaystyle \left\Vert {f}_{n}\right\Vert _{p}<\infty }$, удовлетворяющая условию

${\displaystyle \lim _{k,\ n\to \infty }\int _{\Omega }\left\vert {f}_{k}(x)-{f}_{n}(x)\right\vert ^{p}\,{d\mu \left(x\right)}=0}$

существует функция ${\displaystyle {f}\left(x\right)}$ принадлежащий векторному пространству ${\displaystyle L^{\;\!p}\left(\Omega \right)}$ такой, что

${\displaystyle \lim _{k\to \infty }\int _{\Omega }\left\vert {f}\left(x\right)-{f}_{k}\left(x\right)\right\vert ^{p}\,{d\mu \left(x\right)}=0.}$

Наложение условий ограниченности не только на функцию, но и на ее производные приводит к Соболевские пространства.^[62]

Гильбертовы пространства

Основная статья: Гильбертово пространство

На следующих снимках показано суммирование от 1 до 5 членов при аппроксимации периодической функции (синий) конечной суммой синусоидальных функций (красный).

Полные внутренние пространства продукта известны как Гильбертовы пространства, в честь Дэвид Гильберт.^[63]Гильбертово пространство L²(Ω) с внутренним произведением, задаваемым

${\displaystyle \langle f\ ,\ g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx,}$

куда ${\displaystyle {\overline {g(x)}}}$ обозначает комплексно сопряженный из грамм(Икс),^{[64][№ 12]} это ключевой случай.

По определению в гильбертовом пространстве любая последовательность Коши сходится к пределу. И наоборот, найдя последовательность функций ж_п с желаемыми свойствами, приближающими заданную предельную функцию, не менее важен. Ранний анализ под видом Приближение Тейлора, установил приближение дифференцируемые функции ж полиномами.^[65] Посредством Теорема Стоуна – Вейерштрасса, каждая непрерывная функция на [а, б] может быть аппроксимирован полиномом с любой точностью.^[66] Похожая техника аппроксимации тригонометрические функции обычно называют Разложение Фурье, и широко применяется в технике, см. ниже.^{[требуется разъяснение ]} В более общем плане и в более концептуальном плане теорема дает простое описание того, какие «базовые функции» или, в абстрактных гильбертовых пространствах, каких базовых векторов достаточно для создания гильбертова пространства. ЧАС, в том смысле, что закрытие их промежутка (то есть конечных линейных комбинаций и их пределов) составляет все пространство. Такой набор функций называется основа из ЧАС, его мощность известна как Размерность гильбертова пространства.^{[№ 13]} Теорема не только показывает подходящие базисные функции, достаточные для целей аппроксимации, но и вместе с Процесс Грама – Шмидта, он позволяет построить базис ортогональных векторов.^[67] Такие ортогональные базисы являются обобщением координатных осей в гильбертовом пространстве в конечномерном пространстве. Евклидово пространство.

Решения для различных дифференциальные уравнения можно интерпретировать в терминах гильбертовых пространств. Например, очень многие области физики и техники приводят к таким уравнениям, и часто решения с определенными физическими свойствами используются в качестве базисных функций, часто ортогональных.^[68] В качестве примера из физики зависимость от времени Уравнение Шредингера в квантовая механика описывает изменение физических свойств во времени с помощью уравнение в частных производных, решения которого называются волновые функции.^[69] Определенные значения физических свойств, таких как энергия или импульс, соответствуют собственные значения определенного (линейного) дифференциальный оператор и соответствующие волновые функции называются собственные состояния. В спектральная теорема разлагает линейный компактный оператор действуя на функции через эти собственные функции и их собственные значения.^[70]

Алгебры над полями

Основные статьи: Алгебра над полем и Алгебра Ли

А гипербола, задаваемый уравнением Икс ⋅ у = 1. В координатное кольцо функций на этой гиперболе задается формулой р[Икс, у] / (Икс · у − 1), бесконечномерное векторное пространство над р.

Общие векторные пространства не обладают умножением между векторами. Векторное пространство с дополнительным билинейный оператор определение умножения двух векторов является алгебра над полем.^[71] Многие алгебры происходят из функций на каком-то геометрическом объекте: поскольку функции со значениями в данном поле могут быть умножены поточечно, эти объекты образуют алгебры. Теорема Стоуна – Вейерштрасса, например, основана на Банаховы алгебры которые одновременно являются банаховыми пространствами и алгебрами.

Коммутативная алгебра широко использует кольца многочленов в одной или нескольких переменных, введенных над.^{[требуется разъяснение ]} Их умножение равно как коммутативный и ассоциативный. Эти кольца и их частные составляют основу алгебраическая геометрия, потому что они кольца функций алгебро-геометрических объектов.^[72]

Другой важный пример: Алгебры Ли, которые не являются ни коммутативными, ни ассоциативными, но их отсутствие ограничено ограничениями ([Икс, у] обозначает продукт Икс и у):

• [Икс, у] = −[у, Икс] (антикоммутативность ), и
• [Икс, [у, z]] + [у, [z, Икс]] + [z, [Икс, у]] = 0 (Личность Якоби ).^[73]

Примеры включают векторное пространство п-к-п матрицы, с [Икс, у] = ху − yx, то коммутатор двух матриц, и р³, наделенный перекрестное произведение.

В тензорная алгебра Т (V) является формальным способом добавления продуктов в любое векторное пространство V получить алгебру.^[74] Как векторное пространство оно заполнено символами, называемыми простыми тензоры

v₁ ⊗ v₂ ⊗ ⋯ ⊗ v_п, где степень п меняется.

Умножение дается путем объединения таких символов, налагая распределительный закон при добавлении и требуя, чтобы скалярное умножение коммутировало с тензорным произведением ⊗, почти так же, как с тензорным произведением двух векторных пространств, введенных над.^{[требуется разъяснение ]} В общем, нет никакой связи между v₁ ⊗ v₂ и v₂ ⊗ v₁. Принуждение двух таких элементов к равенству приводит к симметрическая алгебра, а принуждение v₁ ⊗ v₂ = − v₂ ⊗ v₁ дает внешняя алгебра.^[75]

Когда поле, F явно указано, обычно используется термин F-алгебра.

Приложения

Векторные пространства имеют множество приложений, поскольку они часто встречаются в обычных обстоятельствах, а именно везде, где задействованы функции со значениями в каком-либо поле. Они обеспечивают основу для решения аналитических и геометрических задач или используются в преобразовании Фурье. Этот список не является исчерпывающим: существует гораздо больше приложений, например, в оптимизация. В теорема о минимаксе из теория игры утверждение о существовании уникального выигрыша при оптимальной игре всех игроков может быть сформулировано и доказано с использованием методов векторных пространств.^[76] Теория представлений плодотворно переносит хорошее понимание линейной алгебры и векторных пространств в другие математические области, такие как теория групп.^[77]

Распределения

Основная статья: Распределение

А распределение (или же обобщенная функция) - это линейная карта, в которой каждому "тестовая" функция обычно гладкая функция с компактная опора, непрерывно: в над^{[требуется разъяснение ]} По терминологии, пространство распределений является (непрерывным) двойственным пространству пробных функций.^[78] Последнее пространство наделено топологией, учитывающей не только ж сам, но также и все его высшие производные. Стандартный пример - результат интеграции тестовой функции ж над некоторой областью Ω:

${\displaystyle I(f)=\int _{\Omega }f(x)\,dx.}$

Когда Ω = {п}, набор, состоящий из одной точки, сводится к Распределение Дирака, обозначаемый δ, который соответствует пробной функции ж его ценность на п: δ (ж) = ж(п). Распределения - мощный инструмент для решения дифференциальных уравнений. Поскольку все стандартные аналитические понятия, такие как производные, линейны, они естественным образом распространяются на пространство распределений. Следовательно, рассматриваемое уравнение может быть перенесено в пространство распределения, которое больше, чем основное функциональное пространство, так что для решения уравнения доступны более гибкие методы. Например, Функции Грина и фундаментальные решения обычно являются распределениями, а не собственными функциями, и затем могут использоваться для поиска решений уравнения с заданными граничными условиями. Найденное решение затем в некоторых случаях может быть доказано, что оно действительно является истинной функцией и решением исходного уравнения (например, с использованием Теорема Лакса – Милграма, следствие Теорема Рисса о представлении ).^[79]

Анализ Фурье

Основная статья: Анализ Фурье

Уравнение теплопроводности описывает рассеяние физических свойств с течением времени, например, снижение температуры горячего тела, помещенного в более холодную среду (желтый цвет обозначает более холодные области, чем красный).

Решение периодическая функция в сумму тригонометрические функции образует Ряд Фурье, метод, широко используемый в физике и технике.^{[№ 14][80]} Основное векторное пространство обычно Гильбертово пространство L²(0, 2π), для которого функции sin mx и потому mx (м целое число) образуют ортогональный базис.^[81] В Разложение Фурье из L² функция ж является

${\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }\left[a_{m}\cos \left(mx\right)+b_{m}\sin \left(mx\right)\right].}$

Коэффициенты а_м и б_м называются Коэффициенты Фурье из ж, и вычисляются по формулам^[82]

${\displaystyle a_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\cos(mt)\,dt}$, ${\displaystyle b_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(mt)\,dt.}$

Физически функция представлена ​​как суперпозиция из синусоидальные волны а коэффициенты дают информацию о функции частотный спектр.^[83] Также обычно используется комплексная форма ряда Фурье.^[82] Приведенные выше конкретные формулы являются следствием более общего математическая двойственность называется Понтрягинская двойственность.^[84] Применяется к группа р, это дает классическое преобразование Фурье; приложение по физике ответные решетки, где основная группа представляет собой конечномерное вещественное векторное пространство, снабженное дополнительными данными решетка кодирование позиций атомы в кристаллы.^[85]

Ряды Фурье используются для решения краевые задачи в уравнения в частных производных.^[86] В 1822 г. Фурье впервые использовал эту технику для решения уравнение теплопроводности.^[87] Дискретный вариант ряда Фурье можно использовать в отбор проб приложения, в которых значение функции известно только в конечном числе равноудаленных точек. В этом случае ряд Фурье конечен, и его значение во всех точках равно выборочным значениям.^[88] Набор коэффициентов известен как дискретное преобразование Фурье (ДПФ) данной выборочной последовательности. ДПФ - один из ключевых инструментов цифровая обработка сигналов, область, приложения которой включают радар, кодирование речи, сжатие изображений.^[89] В JPEG формат изображения - это приложение тесно связанных дискретное косинусное преобразование.^[90]

В быстрое преобразование Фурье представляет собой алгоритм быстрого вычисления дискретного преобразования Фурье.^[91] Он используется не только для вычисления коэффициентов Фурье, но и с использованием теорема свертки, также для вычисления свертка двух конечных последовательностей.^[92] Они, в свою очередь, применяются в цифровые фильтры^[93] и как стремительный алгоритм умножения для многочленов и больших целых чисел (Алгоритм Шёнхаге – Штрассена ).^[94][95]

Дифференциальная геометрия

Основная статья: Касательное пространство

Касательное пространство к 2-сфера в какой-то момент бесконечная плоскость касается сферы в этой точке.

В касательная плоскость к поверхности в точке естественно является векторным пространством, начало которого отождествляется с точкой контакта. Касательная плоскость - лучшая линейное приближение, или же линеаризация, поверхности в точке.^{[№ 15]} Даже в трехмерном евклидовом пространстве обычно нет естественного способа задать основу для касательной плоскости, и поэтому оно воспринимается как абстрактное векторное пространство, а не как реальное координатное пространство. В касательное пространство является обобщением многомерного дифференцируемые многообразия.^[96]

Римановы многообразия многообразия, касательные пространства которых наделены подходящий внутренний продукт.^[97] Полученный оттуда Тензор кривизны Римана кодирует все искривления многообразия в один объект, который находит применение в общая теория относительности, например, где Тензор кривизны Эйнштейна описывает содержание вещества и энергии пространство-время.^[98][99] Касательное пространство группы Ли может быть естественно задано структурой алгебры Ли и может использоваться для классификации компактные группы Ли.^[100]

Обобщения

Векторные пучки

Основные статьи: Векторный набор и Касательная связка

Лента Мебиуса. Локально это похоже U × р.

А векторный набор представляет собой семейство векторных пространств, непрерывно параметризованных топологическое пространство Икс.^[96] Точнее, векторное расслоение над Икс топологическое пространство E оснащен непрерывной картой

π: E → Икс

так что для каждого Икс в Икс, то волокно π⁻¹(Икс) - векторное пространство. Корпус тусклый V = 1 называется линейный пакет. Для любого векторного пространства V, проекция Икс × V → Икс делает продукт Икс × V в "тривиальное" векторное расслоение. Векторные расслоения над Икс должны быть локально продукт Икс и некоторое (фиксированное) векторное пространство V: для каждого Икс в Икс, Существует район U из Икс такое, что ограничение π на π⁻¹(U) изоморфен^{[№ 16]} в тривиальный пучок U × V → U. Несмотря на их локально тривиальный характер, векторные расслоения могут (в зависимости от формы основного пространства Икс) быть "скрученным" в целом (то есть расслоение не обязательно должно быть (глобально изоморфным) тривиальному расслоению Икс × V). Например, Лента Мебиуса можно рассматривать как пучок линий по окружности S¹ (к идентификация открытых интервалов с реальной линией ). Однако он отличается от цилиндр S¹ × р, потому что последний ориентируемый тогда как первое - нет.^[101]

Свойства определенных векторных пучков предоставляют информацию о лежащем в основе топологическом пространстве. Например, касательный пучок состоит из коллекции касательные пространства параметризованный точками дифференцируемого многообразия. Касательный пучок окружности S¹ глобально изоморфен S¹ × р, поскольку существует ненулевой глобальный векторное поле на S¹.^{[№ 17]} Напротив, теорема о волосатом шарике, нет (касательного) векторного поля на 2-сфера S² который всюду ненулевой.^[102] K-теория изучает классы изоморфизма всех векторных расслоений над некоторым топологическим пространством.^[103] Помимо углубления топологического и геометрического понимания, это имеет чисто алгебраические последствия, такие как классификация конечномерных вещественных алгебры с делением: р, C, то кватернионы ЧАС и октонионы О.

В котангенсный пучок дифференцируемого многообразия состоит в каждой точке многообразия из двойственного к касательному пространству котангенс пространство. Разделы этого пакета известны как дифференциальные одноформы.

Модули

Основная статья: Модуль

Модули должны кольца какие векторные пространства относятся к полям: те же аксиомы, примененные к кольцу р вместо поля F, модули доходности.^[104] Теория модулей по сравнению с теорией векторных пространств осложняется наличием кольцевых элементов, не имеющих мультипликативные обратные. Например, у модулей не должно быть оснований, так как Z-модуль (то есть абелева группа ) Z/2Z показывает; те модули, которые это делают (включая все векторные пространства), известны как бесплатные модули. Тем не менее, векторное пространство можно компактно определить как модуль через звенеть который является поле, элементы которого называются векторами. Некоторые авторы используют термин векторное пространство означать модули над делительное кольцо.^[105] Алгебро-геометрическая интерпретация коммутативных колец через их спектр позволяет развивать такие концепции, как локально бесплатные модули, алгебраический аналог векторных расслоений.

Аффинные и проективные пространства

Основные статьи: Аффинное пространство и Проективное пространство

An аффинная плоскость (голубой) в р³. Это двумерное подпространство, сдвинутое на вектор Икс (красный).

Грубо, аффинные пространства - векторные пространства, происхождение которых не указано.^[106] Точнее, аффинное пространство - это множество с свободный переходный векторное пространство действие. В частности, векторное пространство является аффинным пространством над собой по отображению

V × V → V, (v, а) ↦ а + v.

Если W является векторным пространством, то аффинное подпространство является подмножеством W полученное переносом линейного подпространства V фиксированным вектором Икс ∈ W; это пространство обозначается Икс + V (это смежный из V в W) и состоит из всех векторов вида Икс + v за v ∈ V. Важным примером является пространство решений системы неоднородных линейных уравнений

АИкс = б

обобщение однородного случая б = 0 над.^{[требуется разъяснение ][107]} Пространство решений - это аффинное подпространство Икс + V куда Икс является частным решением уравнения, а V - пространство решений однородного уравнения ( пустое пространство из А).

Множество одномерных подпространств фиксированного конечномерного векторного пространства V известен как проективное пространство; его можно использовать для формализации идеи параллельно линии, пересекающиеся на бесконечности.^[108] Грассманианы и многообразия флагов обобщить это, параметризовав линейные подпространства фиксированной размерности k и флаги подпространств соответственно.

Смотрите также

• Вектор (математика и физика), для списка различных типов векторов

Декартова система координат Градуированное векторное пространство

Метрическое пространство P-вектор Теорема Рисса – Фишера

Космос (математика) Упорядоченное векторное пространство

Примечания

1. Также принято, особенно в физике, обозначать векторы стрелкой вверху: v→.
2. Эта и следующая аксиома относятся к двум различным операциям: скалярному умножению: бv; и умножение полей: ab. Они не утверждают ассоциативность какой-либо операции. Более формально, скалярное умножение - это моноидное действие мультипликативного моноида поля F в векторном пространстве V.
3. Некоторые авторы (например, Браун1991 ) ограничиваем внимание полями р или же C, но большая часть теории остается неизменной для произвольного поля.
4. В индикаторные функции интервалов (которых бесконечно много) линейно независимы, например.
5. Номенклатура происходит от Немецкий "собственный ", что означает собственный или собственный.
6. Смотрите также Разложение Жордана – Шевалле.
7. Обычно это происходит, когда векторное пространство также рассматривается как аффинное пространство. В этом случае линейное подпространство содержит нулевой вектор, а аффинное подпространство не обязательно его содержит.
8. Некоторые авторы (например, Роман2005 ) выберите начать с этого отношение эквивалентности и получить конкретную форму V/W из этого.
9. Из этого требования следует, что топология порождает единообразная структура, Бурбаки1989, гл. II
10. В неравенство треугольника за ${\displaystyle \left\Vert {f+g}\right\Vert _{p}\leq \left\Vert {f}\right\Vert _{p}+\left\Vert {g}\right\Vert _{p}}$обеспечивается Неравенство Минковского. По техническим причинам в контексте функций необходимо идентифицировать функции, которые согласовывают почти всюду получить норму, а не только полунорма.
11. "Многие функции в ${\displaystyle L^{2}}$ меры Лебега, будучи неограниченной, не интегрируется с классическим интегралом Римана. Таким образом, пространства интегрируемых функций Римана не будут полными в ${\displaystyle L^{2}}$норма, и ортогональное разложение к ним не применимо. Это показывает одно из преимуществ интеграции Лебега », - Дадли1989, §5.3, с. 125
12. За п ≠2, L^п(Ω) не является гильбертовым пространством.
13. Базис гильбертова пространства - это не то же самое, что базис в смысле линейной алгебры. над.^{[требуется разъяснение ]} Для различения последний тогда называется Основа Гамеля.
14. Хотя ряд Фурье периодичен, эту технику можно применить к любым L² функция на интервале, считая, что функция периодически продолжается вне интервала. См. Крейсциг1988, п. 601
15. То есть (BSE-3 2001 г. ) ошибка harv: цель отсутствует: CITEREFBSE-32001 (помощь), плоскость, проходящая через точку контакта п такое, что расстояние от точки п₁ на поверхности к плоскости бесконечно маленький по сравнению с расстоянием от п₁ к п в пределе как п₁ подходы п по поверхности.
16. То есть есть гомеоморфизм из π⁻¹(U) к V × U которое ограничивается линейными изоморфизмами между слоями.
17. Линейный пучок, например касательный пучок S¹ тривиально тогда и только тогда, когда существует раздел который никуда не исчезает, см. Husemoller1994, Следствие 8.3. Сечения касательного расслоения просто векторные поля.

Цитаты

1. «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-23.
2. Римский2005, гл. 1, стр. 27
3. «5: векторные пространства». Математика LibreTexts. 2016-02-29. Получено 2020-08-23.
4. Вайсштейн, Эрик В. «Векторное пространство». mathworld.wolfram.com. Получено 2020-08-23.
5. ван дер Варден1993, Гл. 19
6. Бурбаки1998, §II.1.1. Бурбаки называет гомоморфизмами групп ж(а) гомотетии.
7. Бурбаки1969, гл. "Algèbre linéaire et algèbre multinéaire", стр. 78–91.
8. Больцано1804.
9. Мебиус1827.
10. Гамильтон1853.
11. Грассманн2000.
12. Пеано1888, гл. IX.
13. Банах1922.
14. Дорье1995, Мур1995.
15. Lang1987, гл. I.1
16. Lang2002, гл. V.1
17. Lang1993, гл. XII.3., Стр. 335
18. Lang1987, гл. IX.1
19. Lang1987, гл. VI.3.
20. Римский2005, Теорема 1.9, с. 43
21. Blass1984
22. Halpern1966, стр. 670–673
23. Артин1991, Теорема 3.3.13
24. Браун1993, Чт. 3.4.5, п. 291
25. Стюарт1975, Предложение 4.3, с. 52
26. Стюарт1975, Теорема 6.5, с. 74
27. Римский2005, гл. 2, стр. 45
28. Lang1987, гл. IV.4, Следствие, с. 106
29. Lang1987, Пример IV.2.6
30. Lang1987, гл. VI.6
31. Халмос1974, п. 28, Исх. 9
32. Lang1987, Теорема IV.2.1, с. 95
33. Римский2005, Чт. 2.5 и 2.6, п. 49
34. Lang1987, гл. V.1
35. Lang1987, гл. Т.3., Следствие, с. 106
36. Lang1987, Теорема VII.9.8, с. 198
37. Римский2005, гл. 8, стр. 135–156
38. Lang1987, гл. IX.4
39. Римский2005, гл. 8, стр. 140.
40. Римский2005, гл. 1, стр. 29
41. Римский2005, гл. 1, стр. 35 год
42. Римский2005, гл. 3, стр. 64
43. Lang1987, гл. IV.3.
44. Римский2005, гл. 2, стр. 48
45. Mac Lane1998
46. Римский2005, гл. 1. С. 31–32.
47. Lang2002, гл. XVI.1
48. Римский2005, Чт. 14.3. Смотрите также Лемма Йонеды.
49. Шефер и Вольф1999, стр. 204–205
50. Бурбаки2004, гл. 2, стр. 48
51. Римский2005, гл. 9
52. Набер2003, гл. 1.2
53. Treves1967
54. Бурбаки1987
55. Крейсциг 1989, §4.11-5
56. Крейсциг 1989, §1.5-5
57. Choquet1966, Предложение III.7.2
58. Treves1967, п. 34–36
59. Lang1983, Кор. 4.1.2, п. 69
60. Treves1967, гл. 11
61. Treves1967, Теорема 11.2, с. 102
62. Эванс1998, гл. 5
63. Treves1967, гл. 12
64. Деннери и Кшивицки1996, стр.190
65. Lang1993, Чт. XIII.6, стр. 349
66. Lang1993, Чт. III.1.1
67. Choquet1966, Лемма III.16.11
68. Kreyszig1999, Глава 11
69. Гриффитс1995, Глава 1
70. Lang1993, гл. XVII.3
71. Lang2002, гл. III.1, стр. 121
72. Эйзенбуд1995, гл. 1.6
73. Варадараджан1974
74. Lang2002, гл. XVI.7
75. Lang2002, гл. XVI.8
76. Люенбергер1997, §7.13
77. Видеть теория представлений и групповое представительство.
78. Lang1993, Гл. XI.1
79. Эванс1998, Чт. 6.2.1
80. Folland1992, п. 349 ff
81. Гаске и Витомски1999, п. 150
82. Гаске и Витомски1999, §4.5
83. Гаске и Витомски1999, п. 57
84. Лумис1953, Гл. VII
85. Эшкрофт и Мермин1976, Гл. 5
86. Kreyszig1988, п. 667
87. Фурье1822
88. Гаске и Витомски1999, п. 67
89. Ифичор и Джервис2001, стр. 3–4, 11
90. Уоллес1992
91. Ифичор и Джервис2001, п. 132
92. Гаске и Витомски1999, §10.2
93. Ифичор и Джервис2001, стр. 307–310
94. Гаске и Витомски1999, §10.3
95. Шёнхаге и Штрассен1971
96. Спивак1999, гл. 3
97. Jost2005. Смотрите также Лоренцево многообразие.
98. Миснер, Торн и Уиллер1973, гл. 1.8.7, п. 222 и гл. 2.13.5, п. 325
99. Jost2005, гл. 3.1
100. Варадараджан1974, гл. 4.3, теорема 4.3.27
101. Kreyszig1991, §34, с. 108
102. Айзенберг и Гай1979
103. Атья1989
104. Артин1991, гл. 12
105. Грийе, Пьер Антуан. Абстрактная алгебра. Vol. 242. Springer Science & Business Media, 2007.
106. Мейер2000, Пример 5.13.5, с. 436
107. Мейер2000, Упражнение 5.13.15–17, с. 442
108. Coxeter1987

Рекомендации

Алгебра

• Артин, Майкл (1991), Алгебра, Prentice Hall, ISBN  978-0-89871-510-1
• Бласс, Андреас (1984), «Существование базисов подразумевает аксиому выбора», Аксиоматическая теория множеств (Боулдер, Колорадо, 1983), Современная математика, 31, Провиденс, Р.И.: Американское математическое общество, стр. 31–33, МИСТЕР  0763890
• Браун, Уильям А. (1991), Матрицы и векторные пространства, Нью-Йорк: М. Деккер, ISBN  978-0-8247-8419-5
• Ланг, Серж (1987), Линейная алгебра, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-96412-6
• Ланг, Серж (2002), Алгебра, Тексты для выпускников по математике, 211 (Пересмотренное третье изд.), Нью-Йорк: Springer-Verlag, ISBN  978-0-387-95385-4, МИСТЕР  1878556
• Мак-Лейн, Сондерс (1999), Алгебра (3-е изд.), Стр. 193–222, ISBN  978-0-8218-1646-2
• Мейер, Карл Д. (2000), Матричный анализ и прикладная линейная алгебра, СИАМ, ISBN  978-0-89871-454-8
• Роман, Стивен (2005), Продвинутая линейная алгебра, Тексты для выпускников по математике, 135 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-24766-3
• Шпиндлер, Карлхайнц (1993), Абстрактная алгебра с приложениями: Том 1. Векторные пространства и группы., CRC, ISBN  978-0-8247-9144-5
• ван дер Варден, Бартель Леендерт (1993), Алгебра (на немецком языке) (9-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-3-540-56799-8

Анализ

• Бурбаки, Николас (1987), Топологические векторные пространства, Элементы математики, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-3-540-13627-9
• Бурбаки, Николас (2004), Интеграция I, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-3-540-41129-1
• Браун, Мартин (1993), Дифференциальные уравнения и их приложения: введение в прикладную математику, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-97894-9
• BSE-3 (2001) [1994], «Касательная плоскость», Энциклопедия математики, EMS Press
• Шоке, Гюстав (1966), Топология, Бостон, Массачусетс: Академическая пресса
• Деннери, Филипп; Кшивицки, Андре (1996), Математика для физиков, Courier Dover Publications, ISBN  978-0-486-69193-0
• Дадли, Ричард М. (1989), Реальный анализ и вероятность, Серия «Уодсворт и Брукс / Коул по математике», Пасифик Гроув, Калифорния: Уодсворт и Брукс / Коул Продвинутые книги и программное обеспечение, ISBN  978-0-534-10050-6
• Данэм, Уильям (2005), Галерея исчислений, Princeton University Press, ISBN  978-0-691-09565-3
• Эванс, Лоуренс К. (1998), Уравнения с частными производными, Провиденс, Р.И.: Американское математическое общество, ISBN  978-0-8218-0772-9
• Фолланд, Джеральд Б. (1992), Фурье-анализ и его приложения, Брукс-Коул, ISBN  978-0-534-17094-3
• Гаске, Клод; Витомски, Патрик (1999), Фурье-анализ и приложения: фильтрация, численные вычисления, всплески, Тексты по прикладной математике, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-98485-8
• Ifeachor, Emmanuel C .; Джервис, Барри В. (2001), Цифровая обработка сигналов: практический подход (2-е изд.), Харлоу, Эссекс, Англия: Прентис-Холл (опубликовано в 2002 г.), ISBN  978-0-201-59619-9
• Кранц, Стивен Г. (1999), Панорама гармонического анализа, Математические монографии Каруса, Вашингтон, округ Колумбия: Математическая ассоциация Америки, ISBN  978-0-88385-031-2
• Крейсциг, Эрвин (1988), Высшая инженерная математика (6-е изд.), Нью-Йорк: John Wiley & Sons, ISBN  978-0-471-85824-9
• Крейсциг, Эрвин (1989), Вводный функциональный анализ с приложениями, Библиотека Wiley Classics, Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-471-50459-7, МИСТЕР  0992618
• Ланг, Серж (1983), Реальный анализ, Эддисон-Уэсли, ISBN  978-0-201-14179-5
• Ланг, Серж (1993), Реальный и функциональный анализ, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-94001-4
• Лумис, Линн Х. (1953), Введение в абстрактный гармонический анализ, Торонто-Нью-Йорк-Лондон: D. Van Nostrand Company, Inc., стр. X + 190, HDL:2027 / uc1.b4250788
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства. Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN  978-1584888666. OCLC  144216834.
• Шефер, Гельмут Х.; Вольф, Манфред П. (1999). Топологические векторные пространства. GTM. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN  978-1-4612-7155-0. OCLC  840278135.
• Тревес, Франсуа (1967), Топологические векторные пространства, распределения и ядра, Бостон, Массачусетс: Академическая пресса

Исторические ссылки

• Банах, Стефан (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (Об операциях в абстрактных множествах и их применении к интегральным уравнениям)" (PDF), Fundamenta Mathematicae (На французском), 3: 133–181, Дои:10.4064 / FM-3-1-133-181, ISSN  0016-2736
• Больцано, Бернар (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Соображения некоторых аспектов элементарной геометрии) (на немецком)
• Бурбаки, Николас (1969), Éléments d'histoire des mathématiques (Элементы истории математики) (на французском), Париж: Герман
• Дорье, Жан-Люк (1995), «Общий очерк генезиса теории векторного пространства», Historia Mathematica, 22 (3): 227–261, Дои:10.1006 / hmat.1995.1024, МИСТЕР  1347828
• Фурье, Жан Батист Жозеф (1822), Теория аналитик де ла шалёр (на французском), Chez Firmin Didot, père et fils
• Грассманн, Герман (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (на немецком языке), О. Виганд, перепечатка: Грассманн, Герман (2000), Канненберг, Л. (ред.), Теория расширений, переведено Канненбергом, Ллойдом К., Провиденс, Род-Айленд: Американское математическое общество, ISBN  978-0-8218-2031-5
• Гамильтон, Уильям Роуэн (1853), Лекции по кватернионам, Королевская ирландская академия
• Мебиус, Август Фердинанд (1827), Der Barycentrische Calculus: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Барицентрическое исчисление: новая утилита для аналитического обращения с геометрией) (на немецком языке), заархивировано из оригинал на 2006-11-23
• Мур, Грегори Х. (1995), "Аксиоматизация линейной алгебры: 1875–1940", Historia Mathematica, 22 (3): 262–303, Дои:10.1006 / hmat.1995.1025
• Пеано, Джузеппе (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann Preduto dalle Operazioni della Logica Deduttiva (на итальянском языке), Турин
• Пеано, Г. (1901) Formulario mathematico: аксиомы vct через Интернет-архив

Дальнейшие ссылки

• Эшкрофт, Нил; Мермин, Н. Давид (1976), Физика твердого тела, Торонто: обучение Томсона, ISBN  978-0-03-083993-1
• Атья, Майкл Фрэнсис (1989), K-теория, Advanced Book Classics (2-е изд.), Эддисон-Уэсли, ISBN  978-0-201-09394-0, МИСТЕР  1043170
• Бурбаки, Николас (1998), Элементы математики: Алгебра I Главы 1-3, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-3-540-64243-5
• Бурбаки, Николас (1989), Общая топология. Главы 1-4, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-3-540-64241-1
• Коксетер, Гарольд Скотт Макдональд (1987), Проективная геометрия (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-96532-1
• Айзенберг, Мюррей; Гай, Роберт (1979), "Доказательство теоремы о волосатом шарике", Американский математический ежемесячник, 86 (7): 572–574, Дои:10.2307/2320587, JSTOR  2320587
• Эйзенбуд, Дэвид (1995), Коммутативная алгебра, Тексты для выпускников по математике, 150, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-94269-8, МИСТЕР  1322960
• Голдрей, Дерек (1996), Классическая теория множеств: управляемое независимое исследование (1-е изд.), Лондон: Чепмен и Холл, ISBN  978-0-412-60610-6
• Гриффитс, Дэвид Дж. (1995), Введение в квантовую механику, Река Верхний Сэдл, Нью-Джерси: Prentice Hall, ISBN  978-0-13-124405-4
• Халмос, Пол Р. (1974), Конечномерные векторные пространства, Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-90093-3
• Халперн, Джеймс Д. (июнь 1966 г.), "Основы в векторных пространствах и аксиома выбора", Труды Американского математического общества, 17 (3): 670–673, Дои:10.2307/2035388, JSTOR  2035388
• Хьюз-Халлетт, Дебора; Маккаллум, Уильям Дж .; Глисон, Эндрю М. (2013), Исчисление: одно- и многомерное (6-е изд.), Джон Уайли и сыновья, ISBN  978-0470-88861-2
• Хусемоллер, Дейл (1994), Пучки волокна (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-94087-8
• Йост, Юрген (2005), Риманова геометрия и геометрический анализ (4-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-3-540-25907-7
• Крейсциг, Эрвин (1991), Дифференциальная геометрия, Нью-Йорк: Dover Publications, стр. xiv + 352, ISBN  978-0-486-66721-8
• Крейсциг, Эрвин (1999), Высшая инженерная математика (8-е изд.), Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-471-15496-9
• Люенбергер, Дэвид (1997), Оптимизация методами векторного пространства, Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-471-18117-0
• Мак-Лейн, Сондерс (1998), Категории для рабочего математика (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN  978-0-387-98403-2
• Миснер, Чарльз В.; Торн, Кип; Уилер, Джон Арчибальд (1973), Гравитация, У. Х. Фриман, ISBN  978-0-7167-0344-0
• Набер, Грегори Л. (2003), Геометрия пространства-времени Минковского, Нью-Йорк: Dover Publications, ISBN  978-0-486-43235-9, МИСТЕР  2044239
• Шёнхаге, А.; Штрассен, Фолькер (1971), "Schnelle Multiplikation großer Zahlen (быстрое умножение больших чисел)", Вычисление (на немецком), 7 (3–4): 281–292, Дои:10.1007 / bf02242355, ISSN  0010-485X, S2CID  9738629
• Спивак Михаил (1999), Комплексное введение в дифференциальную геометрию (том второй), Хьюстон, Техас: опубликовать или погибнуть
• Стюарт, Ян (1975), Теория Галуа, Чепмен и Холл Математическая серия, Лондон: Чепмен и Холл, ISBN  978-0-412-10800-6
• Варадараджан, В. С. (1974), Группы Ли, алгебры Ли и их представления, Prentice Hall, ISBN  978-0-13-535732-3
• Уоллес, Г. (Февраль 1992 г.), «Стандарт сжатия неподвижных изображений JPEG» (PDF), IEEE Transactions по бытовой электронике, 38 (1): xviii – xxxiv, CiteSeerX  10.1.1.318.4292, Дои:10.1109/30.125072, ISSN  0098-3063, заархивировано из оригинал (PDF) на 2007-01-13, получено 2017-10-25
• Вейбель, Чарльз А. (1994). Введение в гомологическую алгебру. Кембриджские исследования в области высшей математики. 38. Издательство Кембриджского университета. ISBN  978-0-521-55987-4. МИСТЕР  1269324. OCLC  36131259.

внешняя ссылка

• «Векторное пространство», Энциклопедия математики, EMS Press, 2001 [1994]