Биалгебра - Bialgebra

В математика, а биалгебра через поле K это векторное пространство над K что является одновременно единый ассоциативная алгебра и коассоциативная коассоциативная коалгебра. Алгебраические и коалгебраические структуры сделаны совместимыми с еще несколькими аксиомами. В частности, коумножение и графство обе являются алгеброй с единицей гомоморфизмы, или, что то же самое, умножение и единица алгебры равны морфизмы коалгебры. (Эти утверждения эквивалентны, поскольку они выражаются одним и тем же коммутативные диаграммы.)

Подобные биалгебры связаны гомоморфизмами биалгебр. Гомоморфизм биалгебр - это линейная карта это одновременно и алгебра, и гомоморфизм коалгебр.

Как отражено в симметрии коммутативных диаграмм, определение биалгебры таково: самодвойственный, поэтому, если можно определить двойной из B (что всегда возможно, если B конечномерна), то она автоматически является биалгеброй.

Формальное определение

(B, ∇, η, Δ, ε) это биалгебра над K если он имеет следующие свойства:

• B это векторное пространство над K;
• Существуют K-линейные карты (умножение) ∇: B ⊗ B → B (эквивалентно K-многолинейная карта ∇: B × B → B) и (единица) η: K → B, такое что (B, ∇, η) - единичная ассоциативная алгебра;
• Существуют K-линейные отображения (коумножение) Δ: B → B ⊗ B и (count) ε: B → K, такое что (B, Δ, ε) является (коассоциативной) коалгебра;
• условия совместимости, выраженные следующими коммутативные диаграммы:

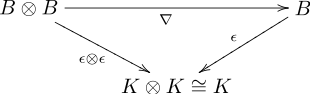
1. Умножение ∇ и коумножение Δ^[1]

   

   где τ: B ⊗ B → B ⊗ B это линейная карта определяется как τ (Икс ⊗ у) = у ⊗ Икс для всех Икс и у в B,

2. Умножение ∇ и счет ε

   

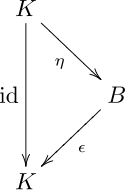
3. Умножение Δ и единица η^[2]

   

4. Единица η и счетчик ε

   

Коассоциативность и счет

В K-линейная карта Δ: B → B ⊗ B является коассоциативный если ${\displaystyle (\mathrm {id} _{B}\otimes \Delta )\circ \Delta =(\Delta \otimes \mathrm {id} _{B})\circ \Delta }$.

В K-линейное отображение ε: B → K это графа, если ${\displaystyle (\mathrm {id} _{B}\otimes \epsilon )\circ \Delta =\mathrm {id} _{B}=(\epsilon \otimes \mathrm {id} _{B})\circ \Delta }$.

Коассоциативность и коассоциативность выражаются коммутативностью следующих двух диаграмм (они являются двойниками диаграмм, выражающих ассоциативность и единицу алгебры):

Условия совместимости

Четыре коммутативные диаграммы можно прочитать как «коумножение и счетчик гомоморфизмы алгебр "или, что то же самое," умножение и единица являются гомоморфизмы коалгебр ».

Эти утверждения приобретут смысл, если мы объясним естественные структуры алгебры и коалгебры во всех задействованных векторных пространствах, кроме B: (K, ∇₀, η₀) очевидным образом является ассоциативной алгеброй с единицей и (B ⊗ B, ∇₂, η₂) - ассоциативная алгебра с единицей и умножением

${\displaystyle \eta _{2}:=(\eta \otimes \eta ):K\otimes K\equiv K\to (B\otimes B)}$

${\displaystyle \nabla _{2}:=(\nabla \otimes \nabla )\circ (id\otimes \tau \otimes id):(B\otimes B)\otimes (B\otimes B)\to (B\otimes B)}$,

так что ${\displaystyle \nabla _{2}((x_{1}\otimes x_{2})\otimes (y_{1}\otimes y_{2}))=\nabla (x_{1}\otimes y_{1})\otimes \nabla (x_{2}\otimes y_{2})}$ или, опуская ∇ и написав умножение как сопоставление, ${\displaystyle (x_{1}\otimes x_{2})(y_{1}\otimes y_{2})=x_{1}y_{1}\otimes x_{2}y_{2}}$;

по аналогии, (K, Δ₀, ε₀) очевидным образом является коалгеброй и B ⊗ B коалгебра со счетчиком и коумножением

${\displaystyle \epsilon _{2}:=(\epsilon \otimes \epsilon ):(B\otimes B)\to K\otimes K\equiv K}$

${\displaystyle \Delta _{2}:=(id\otimes \tau \otimes id)\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)\otimes (B\otimes B)}$.

Тогда диаграммы 1 и 3 говорят, что Δ: B → B ⊗ B является гомоморфизмом унитальных (ассоциативных) алгебр (B,, Η) и (B ⊗ B, ∇₂, η₂)

${\displaystyle \Delta \circ \nabla =\nabla _{2}\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)}$, или просто Δ (ху) = Δ (Икс) Δ (у),

${\displaystyle \Delta \circ \eta =\eta _{2}:K\to (B\otimes B)}$, или просто Δ (1_B) = 1_{B ⊗ B};

диаграммы 2 и 4 говорят, что ε: B → K является гомоморфизмом унитальных (ассоциативных) алгебр (B,, Η) и (K, ∇₀, η₀):

${\displaystyle \epsilon \circ \nabla =\nabla _{0}\circ (\epsilon \otimes \epsilon ):(B\otimes B)\to K}$, или просто ε (ху) = ε (Икс) ε (у)

${\displaystyle \epsilon \circ \eta =\eta _{0}:K\to K}$, или просто ε (1_B) = 1_K.

Эквивалентно диаграммы 1 и 2 говорят, что ∇: B ⊗ B → B является гомоморфизмом (коассоциативных) коассоциативных коалгебр (B ⊗ B, Δ₂, ε₂) и (B, Δ, ε):

${\displaystyle \nabla \otimes \nabla \circ \Delta _{2}=\Delta \circ \nabla :(B\otimes B)\to (B\otimes B),}$

${\displaystyle \nabla _{0}\circ \epsilon _{2}=\epsilon \circ \nabla :(B\otimes B)\to K}$;

диаграммы 3 и 4 говорят, что η: K → B является гомоморфизмом (коассоциативных) коассоциативных коалгебр (K, Δ₀, ε₀) и (B, Δ, ε):

${\displaystyle \eta _{2}\circ \Delta _{0}=\Delta \circ \eta :K\to (B\otimes B),}$

${\displaystyle \eta _{0}\circ \epsilon _{0}=\epsilon \circ \eta :K\to K}$,

куда

${\displaystyle \epsilon _{0}=\epsilon \circ \eta }$.

Примеры

Групповая биалгебра

Примером биалгебры является набор функций из группа грамм (или вообще любой моноид ) к ${\displaystyle \mathbb {R} }$, которое мы можем представить как векторное пространство ${\displaystyle \mathbb {R} ^{G}}$ состоящий из линейных комбинаций стандартных базисных векторов е_грамм для каждого грамм ∈ грамм, который может представлять собой распределение вероятностей над грамм в случае векторов, все коэффициенты которых неотрицательны и суммируются с 1. Примером подходящих операторов коумножения и счетчиков, которые дают коитальную коалгебру, являются

${\displaystyle \Delta (\mathbf {e} _{g})=\mathbf {e} _{g}\otimes \mathbf {e} _{g}\,,}$

который представляет собой создание копии случайная переменная (который мы распространяем на все ${\displaystyle \mathbb {R} ^{G}}$ по линейности), и

${\displaystyle \varepsilon (\mathbf {e} _{g})=1\,,}$

(снова линейно распространяется на все ${\displaystyle \mathbb {R} ^{G}}$), который представляет собой "отслеживание" случайной величины - т.е. забывая значение случайной величины (представленной единственным тензорным фактором), чтобы получить предельное распределение от остальных переменных (остальных тензорных множителей). Учитывая интерпретацию (Δ, ε) в терминах вероятностных распределений, как указано выше, условия согласованности биалгебры сводятся к следующим ограничениям на (∇, η):

1. η - оператор, составляющий нормированное распределение вероятностей, которое не зависит от всех других случайных величин;
2. Произведение ∇ отображает распределение вероятностей двух переменных в распределение вероятностей одной переменной;
3. Копирование случайной величины в распределении η эквивалентно наличию двух независимых случайных величин в распределении η;
4. Получение произведения двух случайных величин и подготовка копии полученной случайной величины имеет такое же распределение, как и подготовка копий каждой случайной величины независимо друг от друга и их попарное умножение.

Пара (∇, η), удовлетворяющая этим ограничениям, является свертка оператор

${\displaystyle \nabla {\bigl (}\mathbf {e} _{g}\otimes \mathbf {e} _{h}{\bigr )}=\mathbf {e} _{gh}\,,}$

снова распространяется на всех ${\displaystyle \mathbb {R} ^{G}\otimes \mathbb {R} ^{G}}$ по линейности; это дает нормализованное распределение вероятностей из распределения двух случайных величин и имеет в качестве единицы дельта-распределение ${\displaystyle \eta =\mathbf {e} _{i}\;,}$ куда я ∈ грамм обозначает единичный элемент группы грамм.

Другие примеры

Другие примеры биалгебр включают тензорная алгебра, который можно превратить в биалгебру, добавив соответствующее коумножение и счетчик; они подробно рассматриваются в этой статье.

Биалгебры часто можно расширить до Алгебры Хопфа, если можно найти подходящий антипод. Таким образом, все алгебры Хопфа являются примерами биалгебр.^[3] Подобные структуры с различной совместимостью между произведением и коумножением или разными типами умножения и коумножения включают: Биалгебры Ли и Алгебры Фробениуса. Дополнительные примеры приведены в статье о коалгебры.

Смотрите также

• Квазибиалгебра

Примечания

1. Дэскэлеску, Нэстэсеску и Райану (2001). Алгебры Хопфа: введение. С. 147 и 148.
2. Дэскэлеску, Нэстэсеску и Райану (2001). Алгебры Хопфа: введение. п. 148.
3. Дэскэлеску, Нэстэсеску и Райану (2001). Алгебры Хопфа: введение. п. 151.

Рекомендации

• Дэскэлеску, Сорин; Нэстэсеску, Константин; Райану, Шербан (2001), Алгебры Хопфа: введение, Чистая и прикладная математика, 235 (1-е изд.), Марсель Деккер, ISBN  0-8247-0481-9.