Тихоновское пространство - Tychonoff space

Аксиомы разделения в топологические пространства
Колмогоров классификация
Т0	(Колмогоров)
Т1	(Фреше)
Т2	(Хаусдорф)
Т2½	(Урысон)
полностью T2	(полностью Хаусдорф)
Т3	(обычный Хаусдорф)
Т3½	(Тихонов)
Т4	(нормальный Хаусдорф)
Т5	(совершенно нормально Хаусдорф)
Т6	(совершенно нормально Хаусдорф)
История

В топология и смежные отрасли математика, Тихоновские пространства и полностью регулярные пространства виды топологические пространства. Эти условия являются примерами аксиомы разделения.

Тихоновские пространства названы в честь Тихонов Андрей Николаевич, чей русский имя (Тихонов) по-разному переводится как «Тихонов», «Тихонов», «Тихонов», «Тихонов» и т. д., которые ввел их в 1930 г. во избежание патологической ситуации Хаусдорфовы пространства единственными непрерывными действительными функциями которого являются постоянные отображения.^[1]

Определения

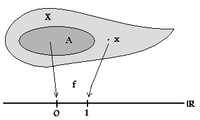
Топологическое пространство ${\displaystyle X}$ называется полностью обычный именно в том случае, если очки могут быть отделенный из замкнутых множеств через (ограниченные) непрерывные действительные функции. Технически это означает: для любого закрытый набор ${\displaystyle A\subseteq X}$ и любой точка ${\displaystyle x\in X\setminus A,}$ Существует а ценный непрерывная функция ${\displaystyle f:X\to \mathbb {R} }$ такой, что ${\displaystyle f(x)=1}$ и ${\displaystyle f\vert _{A}=0.}$ (Эквивалентно можно выбрать любые два значения вместо ${\displaystyle 0}$ и ${\displaystyle 1}$ и даже требовать, чтобы ${\displaystyle f}$ - ограниченная функция.)

Топологическое пространство называется Тихоновское пространство (альтернативно: Т_3½ Космос, или же Т_π Космос, или же полностью T₃ Космос), если это вполне регулярный Пространство Хаусдорфа.

Замечание. Вполне регулярные пространства и тихоновские пространства связаны понятием Колмогоровская эквивалентность. Топологическое пространство является тихоновским тогда и только тогда, когда оно полностью регулярно и Т₀. С другой стороны, пространство является полностью правильным тогда и только тогда, когда его Колмогоровский фактор Тихонов.

Соглашения об именах

В математической литературе применяются разные соглашения, когда речь идет о терминах «полностью регулярные» и «Т» -аксиомы. Определения в этом разделе даны в типичном современном использовании. Некоторые авторы, однако, меняют значения двух видов терминов или используют все термины как синонимы. В Википедии термины «полностью регулярный» и «тихоновский» используются свободно, а использование буквы «Т» обычно избегается. Поэтому в стандартной литературе рекомендуется проявлять осторожность, чтобы выяснить, какие определения использует автор. Подробнее об этом см. История аксиом разделения.

Примеры и контрпримеры

Практически каждое топологическое пространство, изученное в математический анализ тихоновский, или, по крайней мере, полностью регулярный. реальная линия Тихонов по стандарту Евклидова топология. Другие примеры включают:

• Каждый метрическое пространство Тихонов; каждый псевдометрическое пространство полностью регулярный.
• Каждый локально компактный обычное пространство вполне регулярно, поэтому каждое локально компактное хаусдорфово пространство тихоново.
• В частности, каждый топологическое многообразие Тихонов.
• Каждый полностью заказанный набор с топология заказа Тихонов.
• Каждый топологическая группа полностью регулярный.
• Обобщая как метрические пространства, так и топологические группы, каждое однородное пространство полностью регулярный. Верно и обратное: всякое вполне регулярное пространство униформизимо.
• Каждый CW комплекс Тихонов.
• Каждый нормальный регулярное пространство вполне регулярно, и каждое нормальное хаусдорфово пространство тихоново.
• В Самолет Немицкого является примером тихоновского пространства, которое не нормальный.

Характеристики

Сохранение

Полная регулярность и свойство Тихонова хорошо проявляются по отношению к начальные топологии. В частности, полная регулярность сохраняется при выборе произвольных начальных топологий, а свойство Тихонова сохраняется при выборе исходных топологий, разделяющих точки. Следует, что:

• Каждый подпространство вполне регулярного или тихоновского пространства обладает тем же свойством.
• Непустой пространство продукта является полностью регулярным (соответственно Тихоновым) тогда и только тогда, когда каждое фактор-пространство полностью регулярно (соответственно Тихоновское).

Как и все аксиомы разделения, полная регулярность не сохраняется, если взять окончательные топологии. Особенно, частные полностью регулярных пространств не обязательно обычный. Факторы тихоновских пространств даже не должны быть Хаусдорф. Есть закрытые частные Самолет Мура дающие контрпримеры.

Действительные непрерывные функции

Для любого топологического пространства Икс, позволять C(Икс) обозначают семейство вещественнозначных непрерывные функции на Икс и разреши C_б(Икс) быть подмножеством ограниченный вещественнозначные непрерывные функции.

Полностью регулярные пространства можно охарактеризовать тем, что их топология полностью определяется C(Икс) или же C_б(Икс). Особенно:

• Пространство Икс полностью регулярен тогда и только тогда, когда он имеет начальная топология индуцированный C(Икс) или же C_б(Икс).
• Пространство Икс полностью регулярен тогда и только тогда, когда каждое замкнутое множество может быть записано как пересечение семейства нулевые наборы в Икс (т.е. нулевые множества образуют основу для замкнутых множеств Икс).
• Пространство Икс полностью регулярен тогда и только тогда, когда уютные наборы из Икс сформировать основа для топологии Икс.

Для произвольного топологического пространства (Икс, τ) существует универсальный способ связать вполне регулярное пространство с (Икс, τ). Пусть ρ - начальная топология на Икс индуцированный C_τ(Икс) или, что то же самое, топология, порожденная базисом концевых множеств в (Икс, τ). Тогда ρ будет лучший полностью регулярная топология на Икс что грубее, чем τ. Эта конструкция универсальный в том смысле, что любая непрерывная функция

${\displaystyle f:(X,\tau )\to Y}$

в совершенно обычное пространство Y будет продолжаться (Икс, ρ). На языке теория категорий, то функтор который отправляет (Икс, τ) на (Икс, ρ) есть левый смежный к функтору включения CReg → Вершина. Таким образом, категория вполне регулярных пространств CReg это отражающая подкатегория из Вершина, то категория топологических пространств. Принимая Колмогоровские коэффициенты, видно, что подкатегория тихоновских пространств также рефлексивна.

Можно показать, что C_τ(Икс) = C_ρ(Икс) в приведенной выше конструкции так, чтобы кольца C(Икс) и C_б(Икс) обычно изучаются только для вполне регулярных пространств Икс.

Категория настоящийкомпактный Тихоновское пространство антиэквивалентно категории колец C(Икс) (куда Икс вещественнокомпактно) вместе с гомоморфизмами колец как отображениями. Например, можно восстановить Икс из C(Икс) когда Икс (настоящий) компактный. Поэтому алгебраическая теория этих колец является предметом интенсивных исследований. Обширное обобщение этого класса колец, которое все еще напоминает многие свойства тихоновских пространств, но также применимо в действительная алгебраическая геометрия, это класс настоящие замкнутые кольца.

Вложения

Тихоновские пространства - это как раз те пространства, которые могут бытьвстроенный в компактные хаусдорфовы пространства. Точнее, для каждого тихоновского пространства Икс, существует компактное хаусдорфово пространство K такой, что Икс является гомеоморфный в подпространство K.

На самом деле всегда можно выбрать K быть Тихоновский куб (т.е. возможно бесконечное произведение единичные интервалы ). Каждый тихоновский куб компактен по Хаусдорфу вследствие Теорема Тихонова. Поскольку каждое подпространство компактного хаусдорфова пространства тихоновское, у него есть:

Топологическое пространство тихоновское тогда и только тогда, когда оно может быть вложено в тихоновский куб..

Компактификации

Особый интерес представляют те вложения, в которых изображение Икс является плотный в K; их называют Хаусдорфом компактификации из Икс.Для любого вложения тихоновского пространства Икс в компактном хаусдорфовом пространстве K то закрытие изображения Икс в K компактификация ИксВ той же статье 1930 года, где Тихонов определил вполне регулярные пространства, он также доказал, что каждое Тихоновское пространство имеет компактификацию Хаусдорфа.^[2]

Среди этих хаусдорфовых компактификаций есть уникальная «самая общая» компактификация - Каменно-чешская компактификация βИкс.Он характеризуется универсальная собственность что, учитывая непрерывное отображение ж из Икс в любое другое компактное хаусдорфово пространство Y, Существует уникальный непрерывная карта грамм из βИкс к Y что расширяет ж в том смысле, что ж это сочинение из грамм и j.

Единые конструкции

Полная регулярность - это как раз то условие, необходимое для существования однородные конструкции на топологическом пространстве. Другими словами, каждый однородное пространство имеет полностью регулярную топологию и каждое полностью регулярное пространство Икс является униформизируемый. Топологическое пространство допускает разделенную равномерную структуру тогда и только тогда, когда оно тихоновское.

Учитывая совершенно регулярное пространство Икс обычно бывает более одного единообразия на Икс что совместимо с топологией Икс. Однако всегда будет наилучшее совместимое единообразие, называемое прекрасная однородность на Икс. Если Икс тихоновская, то однородную структуру можно выбрать так, чтобы βИкс становится завершение единого пространства Икс.

Цитаты

1. Наричи и Бекенштейн 2011, п. 240.
2. Наричи и Бекенштейн 2011 С. 225–273.

Библиография

• Гиллман, Леонард; Джерисон, Мейер (1960). Кольца непрерывных функций. Тексты для выпускников по математике, № 43 (переиздание Дувра). Нью-Йорк: Springer-Verlag. п. xiii. ISBN  978-048681688-3.
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства. Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN  978-1584888666. OCLC  144216834.
• Уиллард, Стивен (1970). Общая топология (Dover переиздание ред.). Ридинг, Массачусетс: издательство Addison-Wesley Publishing Company. ISBN  0-486-43479-6.