Четверть 5-кубовые соты - Quarter 5-cubic honeycomb

четверть 5 куб. соты
(Нет изображения)
Тип	Равномерные 5-соты
Семья	Четверть гиперкубические соты
Символ Шлефли	q {4,3,3,3,4}
Диаграмма Кокстера-Дынкина	=
5-гранный тип	ч {4,3^3}, час4{4,3^3},
Фигура вершины	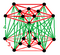Ректифицированная 5-элементная антипризма или растянутый двуатомный 5-симплексный
Группа Кокстера	${\displaystyle {\tilde {D}}_{5}}$×2 = [[3^1,1,3,3^1,1]]
Двойной
Характеристики	вершинно-транзитивный

В пятимерный Евклидова геометрия, то четверть 5 куб. соты равномерное заполнение пространства мозаика (или же соты ). Он имеет половину вершин 5-полукубические соты, а четверть вершин 5-кубовые соты.^[1] Его грани 5-демикубы и запущенные 5-demicubes.

Связанные соты

Эти соты - одна из 20 однородных сот построенный ${\displaystyle {\tilde {D}}_{5}}$ Группа Кокстера, все, кроме трех, повторяются в других семействах по расширенной симметрии, что видно по графической симметрии колец в Диаграммы Кокстера – Дынкина. Перечислены 20 перестановок с их высшим расширенным отношением симметрии:

Соты D5
Расширенный симметрия	Расширенный диаграмма	Расширенный группа	Соты
[3^1,1,3,3^1,1]		${\displaystyle {\tilde {D}}_{5}}$
<[3^1,1,3,3^1,1]> ↔ [3^1,1,3,3,4]	↔	${\displaystyle {\tilde {D}}_{5}}$×21 = ${\displaystyle {\tilde {B}}_{5}}$	, , , , , ,
[[3^1,1,3,3^1,1]]		${\displaystyle {\tilde {D}}_{5}}$×22	,
<2[3^1,1,3,3^1,1]> ↔ [4,3,3,3,4]	↔	${\displaystyle {\tilde {D}}_{5}}$×41 = ${\displaystyle {\tilde {C}}_{5}}$	, , , , ,
[<2[3^1,1,3,3^1,1]>] ↔ [[4,3,3,3,4]]	↔	${\displaystyle {\tilde {D}}_{5}}$×8 = ${\displaystyle {\tilde {C}}_{5}}$×2	, ,

Смотрите также

Регулярные и однородные соты в 5-м пространстве:

• 5-кубовые соты
• 5-полукубчатые соты
• 5-симплексные соты
• Усеченные 5-симплексные соты
• Омнитусеченные 5-симплексные соты

Примечания

1. Кокстер, Правильные и полурегулярные многогранники III, (1988), стр. 318

Рекомендации

• Калейдоскопы: избранные произведения Х. С. М. Кокстер, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN  978-0-471-01003-6 [1]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45] См. Стр. 318. [2]
• Клитцинг, Ричард. "5D Евклидовы мозаики # 5D". x3o3o x3o3o * b3 * e - spaquinoh

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E^2	Равномерная черепица	{3^[3]}	δ3	hδ3	qδ3	Шестиугольный
E^3	Равномерно выпуклые соты	{3^[4]}	δ4	hδ4	qδ4
E^4	Равномерные 4-соты	{3^[5]}	δ5	hδ5	qδ5	24-ячеечные соты
E^5	Равномерные 5-соты	{3^[6]}	δ6	hδ6	qδ6
E^6	Равномерные 6-соты	{3^[7]}	δ7	hδ7	qδ7	222
E^7	Равномерные 7-соты	{3^[8]}	δ8	hδ8	qδ8	133 • 331
E^8	Равномерные 8-соты	{3^[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E^9	Равномерные 9-соты	{3^[10]}	δ10	hδ10	qδ10
Eп-1	Униформа (п-1)-соты	{3^[n]}	δп	hδп	qδп	1k2 • 2k1 • k21