Треугольник Шварца - Schwarz triangle

В геометрия, а Треугольник Шварца, названный в честь Герман Шварц, это сферический треугольник что можно использовать для плитка а сфера возможно перекрытие из-за отражений на его краях. Они были классифицированы в (Шварц 1873 г. ).

В более общем смысле они могут быть определены как мозаика сферы, евклидовой плоскости или гиперболической плоскости. Каждый треугольник Шварца на сфере определяет конечная группа, а на евклидовой или гиперболической плоскости они определяют бесконечную группу.

Треугольник Шварца представлен тремя рациональными числами (п q р) каждый представляет угол при вершине. Значение н / д означает, что угол при вершине d/п полукруга. «2» означает прямоугольный треугольник. Когда это целые числа, треугольник называется Треугольник Мёбиуса, и соответствует не-перекрывающийся тайлинг, а группа симметрии называется группа треугольников. В сфере три треугольника Мёбиуса плюс одно однопараметрическое семейство; на плоскости есть три треугольника Мёбиуса, а в гиперболическом пространстве - трехпараметрическое семейство треугольников Мёбиуса, и нет исключительные объекты.

Пространство решений

Фундаментальный доменный треугольник (п q р), с углами при вершинах π/п, π/q, и π/р, могут существовать в разных пространствах в зависимости от значения суммы обратных значений этих целых чисел:

${\displaystyle {\begin{aligned}{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&>1{\text{ : Sphere}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&=1{\text{ : Euclidean plane}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&<1{\text{ : Hyperbolic plane}}\end{aligned}}}$

Это просто способ сказать, что в евклидовом пространстве внутренние углы треугольника в сумме равны π, а на сфере они составляют угол больше, чем π, а на гиперболическом пространстве они в сумме меньше.

Графическое представление

А Треугольник Шварца графически представлена треугольный граф. Каждый узел представляет собой край (зеркало) треугольника Шварца. Каждое ребро помечено рациональным значением, соответствующим порядку отражения, равным π /угол при вершине.

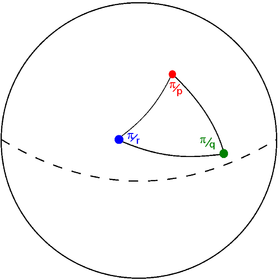Треугольник Шварца (п q р) на сфере

График треугольника Шварца

Ребра порядка 2 представляют собой перпендикулярные зеркала, которые на этой диаграмме можно игнорировать. В Диаграмма Кокстера-Дынкина представляет этот треугольный граф со скрытыми ребрами порядка 2.

А Группа Коксетера можно использовать для более простых обозначений, как (п q р) для циклических графов и (п q 2) = [п,q] для (прямоугольных треугольников) и (п 2 2) = [п]×[].

Список треугольников Шварца

Треугольники Мебиуса для сферы

(2 2 2) или [2,2]	(3 2 2) или [3,2]	...
(3 3 2) или [3,3]	(4 3 2) или [4,3]	(5 3 2) или [5,3]

Треугольники Шварца с целыми числами, также называемые Треугольники Мебиуса, включают одно семейство с одним параметром и три исключительный случаи:

1. [п, 2] или (п 2 2) – Двугранная симметрия,
2. [3,3] или (3 3 2) - Тетраэдрическая симметрия,
3. [4,3] или (4 3 2) - Октаэдрическая симметрия,
4. [5,3] или (5 3 2) - Икосаэдрическая симметрия,

Треугольники Шварца для сферы по плотности

Треугольники Шварца (п q р), сгруппированные по плотность:

Плотность	Двугранный	Тетраэдр	Восьмигранный	Икосаэдр
d	(2 2 п/d)
1		(2 3 3)	(2 3 4)	(2 3 5)
2		(3/2 3 3)	(3/2 4 4)	(3/2 5 5), (5/2 3 3)
3		(2 3/2 3)		(2 5/2 5)
4			(3 4/3 4)	(3 5/3 5)
5		(2 3/2 3/2)	(2 3/2 4)
6		(3/2 3/2 3/2)		(5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7			(2 3 4/3)	(2 3 5/2)
8				(3/2 5/2 5)
9				(2 5/3 5)
10				(3 5/3 5/2), (3 5/4 5)
11			(2 3/2 4/3)	(2 3/2 5)
13				(2 3 5/3)
14			(3/2 4/3 4/3)	(3/2 5/2 5/2), (3 3 5/4)
16				(3 5/4 5/2)
17				(2 3/2 5/2)
18				(3/2 3 5/3), (5/3 5/3 5/2)
19				(2 3 5/4)
21				(2 5/4 5/2)
22				(3/2 3/2 5/2)
23				(2 3/2 5/3)
26				(3/2 5/3 5/3)
27				(2 5/4 5/3)
29				(2 3/2 5/4)
32				(3/2 5/4 5/3)
34				(3/2 3/2 5/4)
38				(3/2 5/4 5/4)
42				(5/4 5/4 5/4)

Треугольники на евклидовой плоскости

(3 3 3)

(4 4 2)

(6 3 2)

Плотность 1:

1. (3 3 3) – 60-60-60 (равносторонний ),
2. (4 4 2) – 45-45-90 (равнобедренная правая),
3. (6 3 2) – 30-60-90,

Плотность 2:

1. (6 6 3/2) - треугольник 120-30-30

Плотность ∞:

1. (4 4/3 ∞)
2. (3 3/2 ∞)
3. (6 6/5 ∞)

Треугольники для гиперболической плоскости

(7 3 2)	(8 3 2)	(5 4 2)
(4 3 3)	(4 4 3)	(∞ ∞ ∞)
Фундаментальные области (п q р) треугольники

Плотность 1:

• (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
• (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
• (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
• (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
• (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
• (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
• (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
• (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
• ...
• (∞ ∞ ∞)

Плотность 2:

• (3/2 7 7), (3/2 8 8), (3/2 9 9) ... (3/2 ∞ ∞)
• (5/2 4 4), (5/2 5 5), (5/2 6 6) ... (5/2 ∞ ∞)
• (7/2 3 3), (7/2 4 4), (7/2 5 5) ... (7/2 ∞ ∞)
• (9/2 3 3), (9/2 4 4), (9/2 5 5) ... (9/2 ∞ ∞)
• ...

Плотность 3:

• (2 7/2 7), (2 9/2 9), (2 11/2 11) ...

Плотность 4:

• (7/3 3 7), (8/3 3 8), (3 10/3 10), (3 11/3 11) ...

Плотность 6:

• (7/4 7 7), (9/4 9 9), (11/4 11 11) ...
• (7/2 7/2 7/2), (9/2 9/2 9/2), ...

Плотность 10:

• (3 7/2 7)

Треугольник Шварца (2 3 7) является наименьшим гиперболическим треугольником Шварца и как таковой представляет особый интерес. Его группа треугольников (точнее, индекс 2 группа фон Дейка изометрий, сохраняющих ориентацию) является (2,3,7) треугольная группа, которая является универсальной группой для всех Группы Гурвица - максимальные группы изометрий Римановы поверхности. Все группы Гурвица являются факторами группы треугольников (2,3,7), и все поверхности Гурвица замощены треугольником Шварца (2,3,7). Наименьшая группа Гурвица - это простая группа порядка 168, вторая по величине неабелева группа. простая группа, который изоморфен PSL (2,7), а ассоциированная поверхность Гурвица (рода 3) является Кляйн квартика.

Треугольник (2 3 8) покрывает Поверхность Больца, высокосимметричная (но не гурвицевская) поверхность рода 2.

Треугольники с одним нецелым углом, перечисленные выше, были сначала классифицированы по Энтони В. Кнапп в.^[1] Список треугольников с несколькими нецелыми углами приведен в.^[2]

Смотрите также

• Функция треугольника Шварца
• Список равномерных многогранников треугольником Шварца
• Символ Wythoff
• Строительство Wythoff
• Равномерный многогранник
• Невыпуклый однородный многогранник
• Плотность (многогранник)
• Тетраэдр Гурса
• Регулярная гиперболическая мозаика
• Равномерные мозаики в гиперболической плоскости

Рекомендации

1. А. В. Кнапп, Двупорожденные фуксовы группы, Мичиганский математический журнал 15 (1968), нет. 3, 289–304
2. Клименко и Сакума, Дискретные подгруппы с двумя образующими в Isom (H 2), содержащие элементы, меняющие ориентацию, Geometriae Dedicata Октябрь 1998 г., том 72, выпуск 3, стр. 247-282

• Кокстер, H.S.M. (1973), Правильные многогранники (Третье изд.), Dover Publications, ISBN  0-486-61480-8, Таблица 3: Треугольники Шварца
• Магнус, Вильгельм (1974), Неуклидовы тесселяции и их группы, Academic Press, ISBN  0080873774
• Шварц, Х.А. (1873 г.), "Ueber diejenigen Fälle in wellchen die Gaussichen hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt", Журнал für die reine und angewandte Mathematik, 1873 (75): 292–335, Дои:10.1515 / crll.1873.75.292, ISSN  0075-4102, S2CID  121698536 (Обратите внимание, что Коксетер называет это «Zur Theorie der hypergeometrischen Reihe», что является коротким заголовком, используемым в заголовках страниц журнала).

• Веннингер, Магнус Дж. (1979), «Введение в понятие многогранной плотности», Сферические модели, Архив CUP, стр.132–134, ISBN  978-0-521-22279-2

внешняя ссылка

• Вайсштейн, Эрик В. «Треугольник Шварца». MathWorld.
• Клитцинг, Ричард. «3D Общий треугольник Шварца (p q r) и обобщенные матрицы инцидентности соответствующих многогранников».