Трехугольная черепица - Trioctagonal tiling

Трехугольная черепица
Модель диска Пуанкаре из гиперболическая плоскость
Тип	Гиперболическая равномерная мозаика
Конфигурация вершины	(3.8)^2
Символ Шлефли	г {8,3} или ${\displaystyle {\begin{Bmatrix}8\\3\end{Bmatrix}}}$
Символ Wythoff	2 | 8 3| 3 3 | 4
Диаграмма Кокстера	или же
Группа симметрии	[8,3], (*832) [(4,3,3)], (*433)
Двойной	Ромбовидная плитка Орден-8-3
Характеристики	Вершинно-транзитивный реберно-транзитивный

В геометрия, то триоктагональная черепица является полуправильным замощением гиперболической плоскости, представляющим собой исправленный Восьмиугольная черепица Order-3. Есть два треугольники и два восьмиугольники поочередно на каждом вершина. Она имеет Символ Шлефли из р{8,3}.

Симметрия

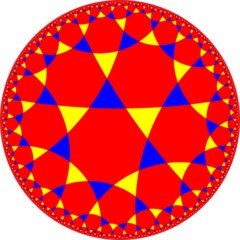Полусимметрия [1^+, 8,3] = [(4,3,3)] может быть изображено с чередованием двух цветов треугольников с помощью диаграммы Кокстера .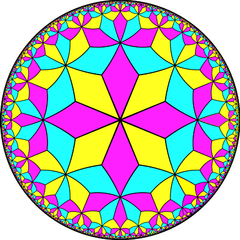

Двойная черепица

Связанные многогранники и мозаики

Из Строительство Wythoff есть восемь гиперболических однородные мозаики который может быть основан на правильной восьмиугольной мозаике.

Нарисовывая плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, существует 8 форм.

Равномерная восьмиугольная / треугольная мозаика [ v т е ]
Симметрия: [8,3], (*832)							[8,3]^+ (832)	[1^+,8,3] (*443)		[8,3^+] (3*4)
{8,3}	т {8,3}	г {8,3}	т {3,8}	{3,8}	рр {8,3} s2{3,8}	tr {8,3}	ср {8,3}	ч {8,3}	час2{8,3}	с {3,8}
								или же	или же
Униформа двойников
V8^3	V3.16.16	V3.8.3.8	V6.6.8	V3^8	V3.4.8.4	V4.6.16	V3^4.8	V (3,4)^3	V8.6.6	V3^5.4

Его также можно сгенерировать из (4 3 3) гиперболических мозаик:

Равномерные (4,3,3) мозаики [ v т е ]
Симметрия: [(4,3,3)], (*433)							[(4,3,3)]^+, (433)
ч {8,3} т0(4,3,3)	г {3,8}^1/2 т0,1(4,3,3)	ч {8,3} т1(4,3,3)	час2{8,3} т1,2(4,3,3)	{3,8}^1/2 т2(4,3,3)	час2{8,3} т0,2(4,3,3)	т {3,8}^1/2 т0,1,2(4,3,3)	с {3,8}^1/2 с (4,3,3)
Униформа двойников
V (3,4)^3	V3.8.3.8	V (3,4)^3	V3.6.4.6	В (3,3)^4	V3.6.4.6	V6.6.8	V3.3.3.3.3.4

Трехоктагональную мозаику можно увидеть в последовательности квазирегулярные многогранники и мозаики:

Квазирегулярные мозаики: (3.n)^2 [ v т е ]
Сим. * n32 [n, 3]	Сферический			Евклид.	Компактная гиперболия.		Paraco.	Некомпактный гиперболический
	*332 [3,3] Тd	*432 [4,3] Очас	*532 [5,3] ячас	*632 [6,3] p6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
Фигура
Фигура
Вершина	(3.3)^2	(3.4)^2	(3.5)^2	(3.6)^2	(3.7)^2	(3.8)^2	(3.∞)^2	(3.12i)^2	(3.9i)^2	(3.6i)^2
Schläfli	г {3,3}	г {3,4}	г {3,5}	г {3,6}	г {3,7}	г {3,8}	г {3, ∞}	г {3,12i}	г {3,9i}	г {3,6i}
Coxeter
Двойные форменные фигуры
Двойной конф.	В (3,3)^2	V (3,4)^2	В (3,5)^2	В (3,6)^2	В (3,7)^2	V (3.8)^2	V (3.∞)^2

Размерное семейство квазирегулярных многогранников и мозаик: (8.n)^2 [ v т е ]
Симметрия * 8n2 [n, 8]	Гиперболический ...						Паракомпакт	Некомпактный
	*832 [3,8]	*842 [4,8]	*852 [5,8]	*862 [6,8]	*872 [7,8]	*882 [8,8]...	*∞82 [∞,8]	[iπ / λ, 8]
Coxeter
Квазирегулярный цифры конфигурация	3.8.3.8	4.8.4.8	8.5.8.5	8.6.8.6	8.7.8.7	8.8.8.8	8.∞.8.∞	8.∞.8.∞

Смотрите также

• Трехгранная черепица - 3.6.3.6 черепица
  • Ромбильная плитка - двойная мозаика V3.6.3.6
• Замощения правильных многоугольников
• Список однородных мозаик

Рекомендации

• Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN  978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
• «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN  0-486-40919-8. LCCN  99035678.

внешняя ссылка

• Вайсштейн, Эрик В. «Гиперболическая мозаика». MathWorld.
• Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре». MathWorld.
• Галерея гиперболических и сферических плиток
• KaleidoTile 3: обучающая программа для создания сферических, плоских и гиперболических мозаик
• Гиперболические плоские мозаики, Дон Хэтч