Список евклидовых однородных мозаик - List of Euclidean uniform tilings

Пример равномерного замощения в Археологический музей Севильи, Севилья, Испания: ромбитогексагональная черепица

В этой таблице показаны 11 выпуклых однородные мозаики (регулярные и полурегулярные) Евклидова плоскость, и их двойственные мозаики.

Есть три обычных^[1] и восемь полурегулярных мозаики в плоскости. Полуправильные мозаики образуют новые мозаики из своих двойников, каждая из которых состоит из неправильных граней одного типа.

Джон Конвей называет эти однородные двойники Каталонская мозаика, параллельно с Каталонский твердый многогранники.

Равномерные мозаики перечислены по их конфигурация вершины, последовательность граней, которые существуют в каждой вершине. Например 4.8.8 означает один квадрат и два восьмиугольника на вершине.

Эти 11 однородных мозаик имеют 32 различных равномерные раскраски. Равномерная раскраска позволяет по-разному раскрашивать многоугольники с одинаковыми сторонами в вершине, сохраняя при этом однородность вершин и трансформационную конгруэнтность между вершинами. (Примечание: некоторые изображения мозаики, показанные ниже, нет цвет-униформа)

Помимо 11 выпуклых однородных мозаик, есть еще 14 невыпуклых мозаик, с помощью звездные многоугольники, и конфигурации вершин обратной ориентации.

Лавес плитки

В книге 1987 г. Плитки и узоры, Бранко Грюнбаум называет однородные по вершинам мозаики Архимедов параллельно с Архимедовы тела. Их двойные мозаики называются Лавес плитки в честь кристаллограф Фриц Лавес.^[2][3] Их еще называют Разбиения Шубникова – Лавеса после Шубников Алексей Васильевич.^[4] Джон Конвей называется равномерными двойниками Каталонская мозаика, параллельно с Каталонский твердый многогранники.

У мозаик Лавеса есть вершины в центрах правильных многоугольников и ребра, соединяющие центры правильных многоугольников с общим ребром. В плитка мозаик Лавеса называются планигоны. Сюда входят 3 правильных плитки (треугольник, квадрат и шестиугольник) и 8 неправильных плиток.^[5] У каждой вершины есть ребра, равномерно расположенные вокруг нее. Трехмерные аналоги планигоны называются стереоэдры.

Эти двойственные мозаики перечислены по их конфигурация лица, количество граней в каждой вершине грани. Например V4.8.8 означает плитки равнобедренного треугольника с одним углом с четырьмя треугольниками и двумя углами с восемью треугольниками. Ориентации вершинных планигонов (до D₁₂ ) согласуются с диаграммами вершин в следующих разделах.

Одиннадцать планигонов

Треугольники				Четырехугольники			Пятиугольники			Шестиугольник
V6^3	V4.8^2	V4.6.12	V3.122	V4^4	В (3,6)^2	V3.4.6.4	V3^2.4.3.4	V3^4.6	V3^3.4^2	V3^6

Выпуклые равномерные мозаики евклидовой плоскости

Все отражающие формы могут быть выполнены Конструкции Wythoff, представлена Символы Wythoff, или же Диаграммы Кокстера-Дынкина, каждый из которых работает на одном из трех Треугольник Шварца (4,4,2), (6,3,2) или (3,3,3) с симметрией, представленной Группы Кокстера: [4,4], [6,3] или [3^[3]]. Альтернативный такие формы, как пренебрежение, также могут быть представлены специальными надписями внутри каждой системы. Только один однородный тайлинг не может быть построен с помощью процесса Уайтхоффа, но может быть создан с помощью удлинение треугольной плитки. Также существует конструкция ортогонального зеркала [∞, 2, ∞], рассматриваемая как два набора параллельных зеркал, образующих прямоугольную фундаментальную область. Если область квадратная, эта симметрия может быть увеличена диагональным зеркалом до семейства [4,4].

Семьи:

• (4,4,2), ${\displaystyle {\tilde {BC}}_{2}}$, [4,4] - Симметрия регулярного квадратная черепица
  • ${\displaystyle {\tilde {I}}_{1}^{2}}$, [∞,2,∞]
• (6,3,2), ${\displaystyle {\tilde {G}}_{2}}$, [6,3] - Симметрия регулярного шестиугольная черепица и треугольная черепица.
  • (3,3,3), ${\displaystyle {\tilde {A}}_{2}}$, [3^[3]]

Семейство групп [4,4]

Равномерные мозаики (Платонический и Архимедовский)	Фигура вершины и двойное лицо Символ (ы) Wythoff Группа симметрии Диаграмма Кокстера (s)	Двойной -однородные мозаики (так называемые Laves или каталонские плитки)
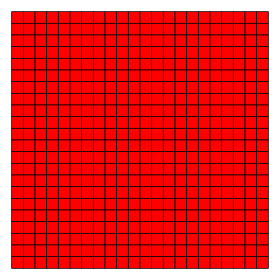Квадратная плитка (кадриль)	4.4.4.4 (или 4^4) 4 | 2 4 p4m, [4,4], (*442)	самодвойственный (кадриль)
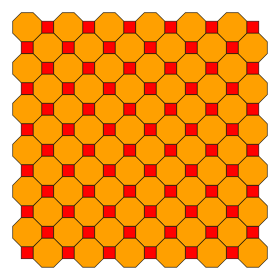Усеченная квадратная мозаика (усеченная кадриль)	4.8.8 2 | 4 4 4 4 2 | p4m, [4,4], (*442) или же	Квадратная плитка Тетракис (кисвадриль)
Плоская квадратная черепица (курносая кадриль)	3.3.4.3.4 | 4 4 2 p4g, [4^+,4], (4*2) или же	Каир пятиугольная черепица (4-кратный пентиль)

Группа [6,3] семейство

Платоновы и архимедовы мозаики	Фигура вершины и двойное лицо Символ (ы) Wythoff Группа симметрии Диаграмма Кокстера (s)	Двойной Лавес плитки
Шестиугольная черепица (гексилль)	6.6.6 (или 6^3) 3 | 6 2 2 6 | 3 3 3 3 | p6m, [6,3], (*632)	Треугольная черепица (дельтиль)
Трехгранная черепица (гексаделтил)	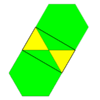(3.6)^2 2 | 6 3 3 3 | 3 p6m, [6,3], (*632) =	Ромбильная плитка (ромбиль)
Усеченная шестиугольная мозаика (усеченный гексилль)	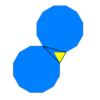3.12.12 2 3 | 6 p6m, [6,3], (*632)	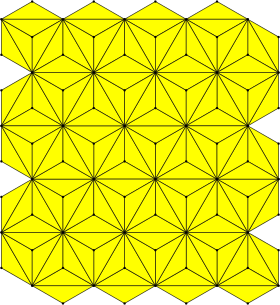Треугольная черепица Triakis (кисделтилле)
Треугольная черепица (дельтиль)	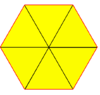3.3.3.3.3.3 (или 3^6) 6 | 3 2 3 | 3 3 | 3 3 3 p6m, [6,3], (*632) =	Шестиугольная черепица (гексилль)
Ромбитрихексагональная черепица (ромбогексаделтилле)	3.4.6.4 3 | 6 2 p6m, [6,3], (*632)	Дельтоидальная трехгексагональная черепица (тетрилль)
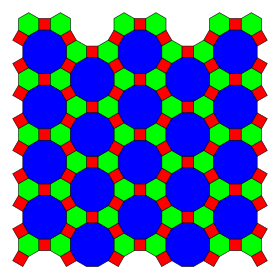Усеченная трехгексагональная мозаика (усеченный гексаделтил)	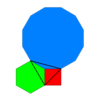4.6.12 2 6 3 | p6m, [6,3], (*632)	Kisrhombille плитка (кисромбиль)
Плоская трехгексагональная черепица (курносый гексилль)	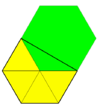3.3.3.3.6 | 6 3 2 p6, [6,3]^+, (632)	Пятиугольная черепица Floret (6-кратный пентиль)

Невитхоффовская равномерная мозаика

Платоновы и архимедовы мозаики	Фигура вершины и двойное лицо Символ (ы) Wythoff Группа симметрии Диаграмма Кокстера	Двойной Лавес плитки
Удлиненная треугольная черепица (изоснуб кадриль)	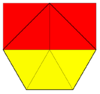3.3.3.4.4 2 | 2 (2 2) см, [∞,2^+,∞], (2*22)	Призматическая пятиугольная черепица (изо (4-) пентилл)

Равномерная окраска

Всего существует 32 однородных раскраски 11 однородных мозаик:

1. Треугольная черепица - 9 расцветок униформы, 4 вайтхоффианских, 5 неуитофианских
   • 
2. Квадратная плитка - 9 раскрасок: 7 уайтхоффианских, 2 неуитофианских
   • 
3. Шестиугольная черепица - 3 раскраски, все wythoffian
   • 
4. Трехгранная черепица - 2 раскраски, оба wythoffian
   • 
5. Плоская квадратная черепица - 2 раскраски, обе чередующиеся вайтоффианские
   • 
6. Усеченная квадратная мозаика - 2 раскраски, оба wythoffian
   • 
7. Усеченная шестиугольная мозаика - 1 окраска, wythoffian
   • 
8. Ромбитрихексагональная черепица - 1 окраска, wythoffian
   • 
9. Усеченная трехгексагональная мозаика - 1 окраска, wythoffian
   • 
10. Плоская шестиугольная черепица - 1 раскраска, чередующаяся wythoffian
    • 
11. Удлиненная треугольная черепица - 1 окраска, неуитофианская
    • 

Смотрите также

• Выпуклые однородные соты - 28 однородных трехмерных мозаик, построенных параллельно выпуклым равномерным евклидовым плоским мозаикам.
• Список мозаик
• Порог перколяции
• Равномерные мозаики в гиперболической плоскости

Рекомендации

1. Новый вид науки [1]
2. Грюнбаум, Бранко; Шепард, Г.С. (1987). Плитки и узоры. В. Х. Фриман и компания. стр.59, 96. ISBN  0-7167-1193-1.
3. Конвей, Джон Х.; Берджел, Хайди; Гудман-Штраус, Хаим (18 апреля 2008 г.). "Глава 21, Называя архимедовы и каталонские многогранники и мозаики, евклидовы плоские мозаики". Симметрии вещей. А. К. Питерс / CRC Press. п. 288. ISBN  978-1-56881-220-5. Архивировано из оригинал 19 сентября 2010 г.
4. Энциклопедия математики: Орбита - уравнение Рэлея, 1991
5. Иванов, А. Б. (2001) [1994], «Планигон», Энциклопедия математики, EMS Press

дальнейшее чтение

• Конвей, Джон Х.; Берджел, Хайди; Гудман-Штраус, Хаим (18 апреля 2008 г.). "Глава 19, Архимедовы мозаики, таблица 19.1 ". Симметрии вещей. А. К. Питерс / CRC Press. ISBN  978-1-56881-220-5. Архивировано из оригинал 19 сентября 2010 г.
• Кокстер, H.S.M.; Лонге-Хиггинс, М.; Миллер, J.C.P. (1954). «Равномерные многогранники». Фил. Пер. 246 А: 401–450.
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN  0-486-23729-X. (Раздел 2–3 Круговые упаковки, плоские мозаики и сетиС. 34–40).
• Асаро, Лаура; Хайд, Джон; Дженсен, Мелани; Манн, Кейси; Шредер, Тайлер. «Равномерный край-c-раскраски архимедовых плиток " (PDF). Вашингтонский университет. (Кейси Манн из Вашингтонского университета )
• Грюнбаум, Бранко; Шепард, Джеффри (Ноябрь 1977 г.). «Замощения правильными многоугольниками» (PDF).
• Сеймур, Дейл; Бриттон, Джилл (1989). Введение в мозаику. Публикации Дейла Сеймура. стр.50–57, 71-74. ISBN  978-0866514613.

внешняя ссылка

• Вайсштейн, Эрик В. «Равномерная тесселяция». MathWorld.
• Равномерные мозаики на плоскости Евклида
• Мозаика на плоскости
• Мир мозаики Дэвида Бейли
• k-однородные мозаики
• п-однородные мозаики