Стереоэдр - Stereohedron
В геометрия и кристаллография, а стереоэдр это выпуклый многогранник который заполняет пространство изоэдрально, что означает, что симметрии мозаики превратить любую копию стереоэдра в любую другую копию.
Двумерные аналоги стереоэдров называются планигоны. Высшее измерение многогранники тоже могут быть стереоэдрами, а точнее их называть стереотопы.
Плезиоэдры
Подмножество стереоэдров называют плезиоэдры, определяемый как Клетки Вороного симметричной Набор Delone.
Параллелоэдры являются плезиоэдрами, заполняющими пространство только за счет трансляции. Края здесь окрашены как параллельные векторы.
 |  |  |  |  |
| куб | шестиугольная призма | ромбический додекаэдр | удлиненный додекаэдр | усеченный октаэдр |
Другие периодические стереоэдры
В катоптрическая мозаика содержат ячейки стереоэдров. Двугранные углы являются целыми делителями 180 ° и раскрашены по порядку. Первые три являются фундаментальными областями , , и симметрия, представленная Диаграммы Кокстера-Дынкина: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() и
и ![]()
![]()
![]() . полусимметрия , и симметрия четверти.
. полусимметрия , и симметрия четверти.
Любые заполняющие пространство стереоэдры с элементами симметрии могут быть рассеченный на более мелкие идентичные ячейки, которые также являются стереоэдрами. Модификаторы имени ниже, половина, четверть и восьмой представляют такие разрезы.
| Лица | 4 | 5 | 6 | 8 | 12 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | Тетраэдры | Квадратная пирамида | Треугольная бипирамида | Куб | Октаэдр | Ромбический додекаэдр | |||||||
| Изображений | 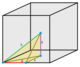 1/48 (1) |  1/24 (2) |  1/12 (4) |  1/12 (4) |  1/24 (2) |  1/6 (8) | 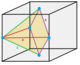 1/6 (8) |  1/12 (4) |  1/4 (12) |  1 (48) |  1/2 (24) |  1/3 (16) |  2 (96) |
| Симметрия (порядок) | C1 1 | C1v 2 | D2d 4 | C1v 2 | C1v 2 | C4в 8 | C2v 4 | C2v 4 | C3в 6 | Очас 48 | D3D 12 | D4ч 16 | Очас 48 |
| Соты | Восьмая пирамидилла | Пирамидилла треугольная | Сплюснутый тетраэдр | Полупирамидилла | Квадратный квартал пирамидилли | Пирамидиль | Половинчатый октаэдр | Четверть сплющенный октаэдр | Четверть кубиля | Cubille | Сплюснутый кубиль | Сплюснутый октаэдр | Додекаэдрил |
Другие выпуклые многогранники, которые являются стереоэдрами, но не параллелоэдрами или плезиоэдрами, включают гиробифастигий.
| Лица | 8 | 10 | 12 | |
|---|---|---|---|---|
| Симметрия (порядок) | D2d (8) | D4ч (16) | ||
| Изображений |  | 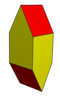 |  |  |
| Клетка | Gyrobifastigium | Удлиненный гиробифастигий | Десятка бриллиантов | Удлиненный квадратная бипирамида |
Апериодические стереоэдры
В Плитка Шмитта – Конвея – Данцера, выпуклый многогранник, покрывающий пространство, не является стереоэдром, потому что все его мозаики апериодический.
Рекомендации
- Иванов, А. Б. (2001) [1994], «Стереоэдр», Энциклопедия математики, EMS Press
- Б. Н. Делоне, Н. Н. Сандакова, Теория стереоэдров Труды Матем. Inst. МИАН, 64 (1961) с. 28–51.
- Гольдберг, Майкл Три бесконечных семейства тетраэдрических заполнителей пространства Журнал комбинаторной теории A, 16, стр. 348–354, 1974.
- Гольдберг, Майкл Пентаэдры, заполняющие пространство, Журнал комбинаторной теории, серия A, том 13, выпуск 3, ноябрь 1972 г., страницы 437-443 [1] PDF
- Гольдберг, Майкл Заполняющие пространство пентаэдры II, Журнал комбинаторной теории 17 (1974), 375–378. PDF
- Гольдберг, Майкл О заполняющих пространство гексаэдрах Геом. Dedicata, июнь 1977 г., том 6, выпуск 1, стр. 99–108 [2] PDF
- Гольдберг, Майкл О заполняющих пространство гептаэдрах Geometriae Dedicata, июнь 1978 г., том 7, выпуск 2, стр 175–184 [3] PDF
- Гольдберг, Майкл Выпуклые многогранные пространства-заполнители более чем двенадцатью гранями. Геом. Дедиката 8, 491-500, 1979.
- Гольдберг, Майкл О заполняющих пространство октаэдрах, Geometriae Dedicata, январь 1981 г., том 10, выпуск 1, стр. 323–335 [4] PDF
- Гольдберг, Майкл О заполняющих пространство декаэдрах. Структурная топология, 1982, номер. Тип 10-II PDF
- Гольдберг, Майкл О заполняющих пространство эннеаэдрах Geometriae Dedicata, июнь 1982 г., том 12, выпуск 3, стр. 297–306 [5] PDF



