Треугольная бипирамида - Triangular bipyramid

Для соответствующей молекулярной геометрической структуры см. Геометрия молекулы тригональной бипирамиды.

Треугольная бипирамида
Тип	Бипирамида и Джонсон J11 - J12 - J13
Лица	6 треугольники
Края	9
Вершины	5
Символ Шлефли	{ } + {3}
Диаграмма Кокстера
Группа симметрии	D3ч, [3,2], (* 223) порядок 12
Группа вращения	D3, [3,2]^+, (223), порядок 6
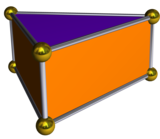
Двойной многогранник	Треугольная призма
Конфигурация лица	V3.4.4
Свойства	Выпуклый, лицо переходный

3D модель треугольной бипирамиды

Сеть

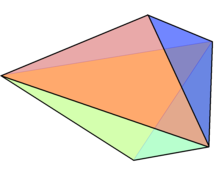
В геометрия, то треугольный бипирамида (или дипирамида) является разновидностью шестигранник, будучи первым в бесконечном множестве лицо переходный бипирамиды. Это двойной из треугольная призма с 6 гранями равнобедренного треугольника.

Как следует из названия, его можно построить, соединив два тетраэдры по одному лицу. Хотя все его лица конгруэнтный и твердое тело лицо переходный, это не Платоново твердое тело потому что некоторые вершины примыкают три грани, а остальные примыкают к четырем.

Бипирамида, все шесть граней которой равносторонние треугольники один из Твердые тела Джонсона, (J₁₂). А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1] Как твердое тело Джонсона со всеми гранями равносторонних треугольников, оно также является дельтаэдр.

Формулы

Следующие формулы для рост (${\displaystyle H}$), площадь поверхности (${\displaystyle A}$) и объем (${\displaystyle V}$) можно использовать, если все грани правильные, с длиной ребра ${\displaystyle L}$:^[2]

${\displaystyle H=L\cdot {\frac {2{\sqrt {6}}}{3}}\approx L\cdot 1.632993162}$

${\displaystyle A=L^{2}\cdot {\frac {3{\sqrt {3}}}{2}}\approx L^{2}\cdot 2.598076211}$

${\displaystyle V=L^{3}\cdot {\frac {\sqrt {2}}{6}}\approx L^{3}\cdot 0.235702260}$

Двойной многогранник

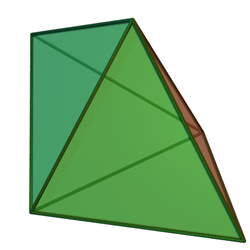
Двойственный многогранник треугольной бипирамиды - это треугольная призма, с пятью гранями: два параллельных равносторонних треугольника, соединенных цепочкой из трех прямоугольников. Хотя треугольная призма имеет форму, которая представляет собой однородный многогранник (с квадратными гранями), двойственная к твердой форме Джонсона бипирамида имеет прямоугольную, а не квадратную форму. лица и не единообразны.

Двойная треугольная бипирамида	Чистая двойная

Связанные многогранники и соты

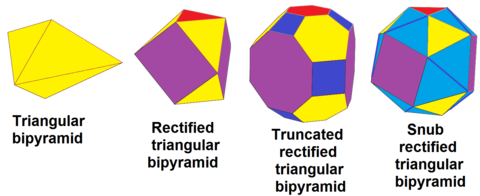
В треугольная бипирамида, dt {2,3}, могут быть последовательно исправленный, rdt {2,3}, усеченный, trdt {2,3} и чередующиеся (пренебрежительно ), srdt {2,3}:

В треугольная бипирамида может быть построен увеличение меньших, в частности, двух обычных октаэдры с 3 треугольными бипирамидами, добавленными по сторонам, и 1 тетраэдром сверху и снизу. В этом многограннике 24 равносторонний треугольник лица, но это не Джонсон солид потому что у него компланарные грани. Это компланарный 24-х треугольник. дельтаэдр. Этот многогранник существует как увеличение клеток в спиральные чередующиеся кубические соты. Треугольные многогранники большего размера могут быть созданы аналогичным образом, например, 9, 16 или 25 треугольников на большую грань треугольника, рассматриваемую как сечение треугольная черепица.

Треугольная бипирамида может образовывать мозаика пространства с участием октаэдры или с усеченные тетраэдры.^[3]

Слои форменной одежды четверть кубических сот можно сдвинуть, чтобы объединить правильные тетраэдрические ячейки в треугольные бипирамиды.

В спиральные четырехгранно-октаэдрические соты имеет пары смежных правильных тетраэдров, которые можно рассматривать как треугольные бипирамиды.

При проецировании на сферу он напоминает соединение тригональный осоэдр и тригональный диэдр. Он является частью бесконечного ряда двойственных парных соединений правильных многогранников, проецируемых на сферы. Треугольную бипирамиду можно назвать дельтовидный шестигранник для согласованности с другими твердыми телами в серии, хотя «дельтовидные тела» в данном случае являются треугольниками, а не воздушными змеями, поскольку угол от диэдра составляет 180 градусов.

*п42 мутации симметрии двойных расширенных мозаик: V3.4.п.4

Симметрия *п32 [n, 3]	Сферический				Евклид.	Компактная гиперб.		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Рисунок Конфиг.	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4

Смотрите также

• Тригональная бипирамидная молекулярная геометрия

«Обычное» правое (симметричное) п-гональный бипирамиды:

имя	Дигональная бипирамида	Треугольная бипирамида (J12)	Квадратная бипирамида (O)	Пятиугольная бипирамида (J13)	Гексагональная бипирамида	Гептагональная бипирамида	Восьмиугольная бипирамида	Эннеагональная бипирамида	Десятиугольная бипирамида	...	Апейрогональная бипирамида
Многогранник образ										...
Сферическая черепица образ										Плоская черепица образ
Конфигурация лица	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Диаграмма Кокстера										...

использованная литература

1. Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, Г-Н  0185507, Zbl  0132.14603.
2. Сапинья, Р. "Площадь и объем твердого Джонсона Джо". Problemas y Ecuaciones (на испанском). ISSN  2659-9899. Получено 2020-09-01.
3. http://w Woodenpolyhedra.web.fc2.com/J12.html

внешние ссылки

• Эрик В. Вайсштейн, Треугольная дипирамида (Джонсон солид ) в MathWorld.
• Обозначение Конвея для многогранников Попробуйте: dP3