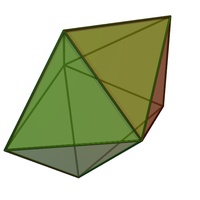
Пятиугольная бипирамида - Pentagonal bipyramid

Пятиугольная бипирамида
Тип	Бипирамида и Джонсон J12 - J13 - J14
Лица	10 треугольники
Края	15
Вершины	7
Символ Шлефли	{ } + {5}
Диаграмма Кокстера
Группа симметрии	D5ч, [5,2], (* 225), порядок 20
Группа вращения	D5, [5,2]^+, (225), порядок 10
Двойной многогранник	пятиугольная призма
Конфигурация лица	V4.4.5
Характеристики	выпуклый, лицо переходный, (дельтаэдр )

Джонсон солид Джо

сеть

В геометрия, то пятиугольник бипирамида (или же дипирамида) является третьим из бесконечного множества лицо переходный бипирамиды. Каждая бипирамида - это двойной из однородная призма.

Хотя это является лицо переходный, это не Платоново твердое тело потому что некоторые вершины есть четыре лица встреча и другие имеют пять лиц.

Характеристики

Если лица равносторонние треугольники, это дельтаэдр и Джонсон солид (J₁₃). Это можно рассматривать как два пятиугольные пирамиды (J₂) связаны своими базами.

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1]

Пятиугольная дипирамида 4-связный, что означает, что нужно удалить четыре вершины, чтобы разъединить оставшиеся вершины. Это один из четырех 4-х соединенных симплициальный хорошо покрытый многогранники, что означает, что все максимальные независимые множества его вершин имеют одинаковый размер. Остальные три многогранника с этим свойством являются правильный октаэдр, то курносый дисфеноид, и неправильный многогранник с 12 вершинами и 20 треугольными гранями.^[2]

Формулы

Следующие формулы для высота (${\displaystyle H}$), площадь поверхности (${\displaystyle A}$) и объем (${\displaystyle V}$) можно использовать, если все грани правильные, с длиной ребра ${\displaystyle L}$:^[3]

${\displaystyle H=L\cdot {\sqrt {2-{\frac {2}{\sqrt {5}}}}}\approx L\cdot 1.0514622242}$

${\displaystyle A=L^{2}\cdot {\frac {5{\sqrt {3}}}{2}}\approx L^{2}\cdot 4.330127019}$

${\displaystyle V=L^{3}\cdot {\frac {5+{\sqrt {5}}}{12}}\approx L^{3}\cdot 0.6030056648}$

Сферическая пятиугольная бипирамида

Связанные многогранники

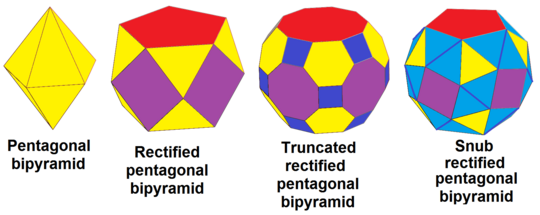
В пятиугольная бипирамида, dt {2,5}, могут быть последовательно исправленный, rdt {2,5}, усеченный, trdt {2,5} и чередовались (пренебрежительно ), srdt {2,5}:

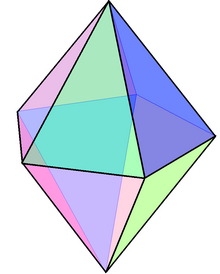
Двойником твердой пятиугольной бипирамиды Джонсона является пятиугольная призма, с 7 гранями: 5 прямоугольных граней и 2 пятиугольника.

Двойная пятиугольная бипирамида	Чистая двойная

Смотрите также

• Пентагональная бипирамидальная молекулярная геометрия

«Обычное» правое (симметричное) п-гональный бипирамиды:

Имя	Дигональная бипирамида	Треугольная бипирамида (J12)	Квадратная бипирамида (O)	Пятиугольная бипирамида (J13)	Гексагональная бипирамида	Гептагональная бипирамида	Восьмиугольная бипирамида	Эннеагональная бипирамида	Десятиугольная бипирамида	...	Апейрогональная бипирамида
Многогранник изображение										...
Сферическая черепица изображение										Плоская черепица изображение
Конфигурация лица	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Диаграмма Кокстера										...

Рекомендации

1. Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР  0185507, Zbl  0132.14603.
2. Финбоу, Артур С .; Hartnell, Bert L .; Новаковски, Ричард Дж .; Пламмер, Майкл Д. (2010), «О хорошо покрытых триангуляциях. III», Дискретная прикладная математика, 158 (8): 894–912, Дои:10.1016 / j.dam.2009.08.002, МИСТЕР  2602814.
3. Сапинья, Р. "Площадь и объем твердого Джонсона Джо". Problemas y ecuaciones (на испанском). ISSN  2659-9899. Получено 2020-09-04.

внешняя ссылка

• Эрик В. Вайсштейн, Пентагональная дипирамида (Дипирамида ) в MathWorld.
• Обозначение Конвея для многогранников Попробуйте: dP5