Bilunabirotunda - Bilunabirotunda
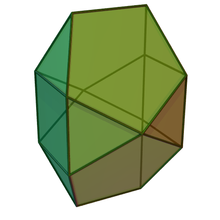
| Bilunabirotunda | |
|---|---|
 | |
| Тип | Джонсон J90 - J91 - J92 |
| Лица | 2x4 треугольники 2 квадраты 4 пятиугольники |
| Края | 26 |
| Вершины | 14 |
| Конфигурация вершины | 4(3.52) 8(3.4.3.5) 2(3.5.3.5) |
| Группа симметрии | D2ч |
| Двойной многогранник | - |
| Характеристики | выпуклый |
| Сеть | |
 | |

В геометрия, то билунабиротонда один из Твердые тела Джонсона (J91).
А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.[1]
Это одно из простейших тел Джонсона, которое не возникает в результате манипуляций "вырезать и вставить" Платонический и Архимедов твердые тела.
Однако он имеет сильную связь с икосододекаэдр, архимедово твердое тело. Любой из двух кластеров из двух пятиугольников и двух треугольников можно выровнять с конгруэнтным участком граней на икосододекаэдре. Если две двунабиротонды выровнены таким образом на противоположных сторонах икосододекаэдра, то две вершины двунабиротонды встречаются в самом центре икосододекаэдра.
Две другие группы граней билунабиротонды, люны (каждый луна с двумя треугольниками, примыкающими к противоположным сторонам одного квадрата), можно выровнять по конгруэнтному участку граней на ромбикосододекаэдр. Если две двунабиротонды выровнены таким образом на противоположных сторонах ромбикосододекаэдра, то между двунабиротондами в самом центре ромбикосододекаэдра можно поместить куб.
Каждую из двух пар смежных пятиугольников (каждая пара пятиугольников, имеющих общую границу) может быть выровнена с пятиугольными гранями икосаэдр с уменьшенным метабидом также.
Двунабиротонда имеет слабую связь с кубооктаэдр, поскольку он может быть создан заменой четырех квадратных граней кубооктаэдра на пятиугольники.

Декартовы координаты
Следующее определяет вершины билунабиротонды с центром в начале координат с длиной ребра 1:
куда это золотое сечение.
Связанные многогранники и соты
Шесть bilunabirotundae могут быть увеличены вокруг куба с помощью пиритоэдрическая симметрия. Б. М. Стюарт обозначил эту модель с шестью билунабиротондами как 6J91(П4).[2]
Билунабиротонда может использоваться с правильным додекаэдром и кубом в качестве заполняющих пространство сот.
 |  Соты для заполнения пространства |  6 билунобиротондов вокруг куба |
внешняя ссылка
- ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР 0185507, Zbl 0132.14603.
- ^ Б. М. Стюарт, Приключения среди тороидов: исследование квазивыпуклых, апланарных, туннельных ориентированных многогранников положительного рода, имеющих правильные грани с непересекающимися внутренностями (1980) ISBN 978-0686119364, (стр.127, 2-е изд.) многогранник 6J91(П4).




