Дисфеноцингулум - Disphenocingulum

Дисфеноцингулум
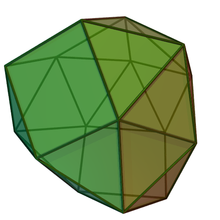Тип	Джонсон J89 - J90 - J91
Лица	4 + 2x8 треугольники 4 квадраты
Края	38
Вершины	16
Конфигурация вершины	4(3^2.4^2) 4(3^5) 8(3^4.4)
Группа симметрии	D2d
Двойной многогранник	Дисфеноид усеченный курносый ордена-5
Характеристики	выпуклый
Сеть

3D модель дифеноцингулюма

В геометрия, то дифеноцингулум или же pentakis удлиненный gyrobifastigium один изТвердые тела Джонсона (J₉₀Это одно из простейших тел Джонсона, которые не возникают в результате манипуляций "вырезать и вставить" Платонический и Архимедов твердые тела.

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1]

Декартовы координаты

Пусть a ≈ 0,76713 будет вторым наименьшим положительным корнем из многочлен

${\displaystyle 256x^{12}-512x^{11}-1664x^{10}+3712x^{9}+1552x^{8}-6592x^{7}+1248x^{6}+4352x^{5}-2024x^{4}-944x^{3}+672x^{2}-24x-23}$

и ${\displaystyle h={\sqrt {2+8a-8a^{2}}}}$ и ${\displaystyle c={\sqrt {1-a^{2}}}}$.

Потом, Декартовы координаты дифеноцингулюма с длиной ребра 2 задаются объединением орбит точек

${\displaystyle (1,2a,{\frac {h}{2}}),(1,0,2c+{\frac {h}{2}}),(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}})}$

под действием группа генерируется отражениями относительно плоскости xz и плоскости yz.^[2]

Рекомендации

1. Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР  0185507, Zbl  0132.14603.
2. Тимофеенко, А.В. (2009-10-17). «Неплатоновые и неархимедовы несоставные многогранники». Журнал математических наук. 162 (5): 710–729. Дои:10.1007 / s10958-009-9655-0. ISSN  1072-3374. S2CID  120114341.

внешняя ссылка

• Эрик В. Вайсштейн, Дисфеноцингулум (Джонсон солид ) в MathWorld.