Квадрат ортобикупола - Square orthobicupola

Квадрат ортобикупола
Тип	Джонсон J27 - J28 - J29
Лица	8 треугольники 2+8 квадраты
Края	32
Вершины	16
Конфигурация вершины	8(3^2.4^2) 8(3.4^3)
Группа симметрии	D4ч
Двойной многогранник	-
Характеристики	выпуклый
Сеть

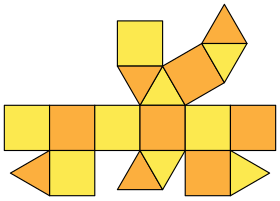В геометрия, то квадратный ортобикупола один из Твердые тела Джонсона (J₂₈). Как следует из названия, его можно построить, соединив два квадратные купола (J₄) вдоль их восьмиугольный основания, совпадающие как лица. Поворот одного купола на 45 градусов до соединения дает квадратная гиробикупола (J₂₉).

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1]

В квадратный ортобикупола второй в бесконечном наборе ортобикуполы.

Квадратный ортобикупол можно удлинить, вставив восьмиугольная призма между двумя куполами, чтобы получить ромбокубооктаэдр, или рухнул из-за удаления неправильного шестиугольная призма дать удлиненная квадратная дипирамида (J₁₅), который сам по себе является просто удлиненным октаэдр.

Связанные многогранники и соты

Квадратный ортобикупол образует заполняющее пространство соты с тетраэдры; с кубики и кубооктаэдр; с тетраэдрами и кубиками; с квадратные пирамиды, тетраэдры и различные комбинации кубов, удлиненные квадратные пирамиды и / или удлиненные квадратные бипирамиды.^[2]

Рекомендации

1. Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР  0185507, Zbl  0132.14603.
2. http://w Woodenpolyhedra.web.fc2.com/J28.html

внешняя ссылка

• Эрик В. Вайсштейн, Квадрат ортобикупола (Джонсон солид ) в MathWorld.