Sphenomegacorona - Sphenomegacorona

Sphenomegacorona
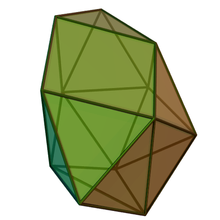Тип	Джонсон J87 - J88 - J89
Лица	16 треугольники 2 квадраты
Края	28
Вершины	12
Конфигурация вершины	2(3^4) 2(3^2.4^2) 2x2 (3^5) 4(3^4.4)
Группа симметрии	C2v
Двойной многогранник	-
Характеристики	выпуклый
Сеть

3D модель сфеномегакороны

В геометрия, то сфеномегакорона один изТвердые тела Джонсона (J₈₈Это одно из простейших тел Джонсона, которые не возникают в результате манипуляций "вырезать и вставить" Платонический и Архимедов твердые тела.

А Джонсон солид один из 92 строго выпуклый многогранники который состоит из правильный многоугольник лица, но не униформа многогранники (т. е. не Платоновы тела, Архимедовы тела, призмы, или же антипризмы ). Их назвали Норман Джонсон, которые впервые перечислили эти многогранники в 1966 году.^[1]

Джонсон использует приставку клиновидно- для обозначения клиновидного комплекса, образованного двумя соседними люны, луна, являющаяся квадрат с равносторонние треугольники прикреплены с противоположных сторон. Точно так же суффикс -мегакорона относится к короноподобному комплексу из 12 треугольников, в отличие от меньшего треугольного комплекса, который делает сфенокорона. Соединение обоих комплексов вместе приводит к sphenomegacorona.^[1]

Декартовы координаты

Позволять k ≈ 0,59463 - наименьший положительный корень из многочлен

${\displaystyle 1680x^{16}-4800x^{15}-3712x^{14}+17216x^{13}+1568x^{12}-24576x^{11}+2464x^{10}+17248x^{9}}$

${\displaystyle {}-3384x^{8}-5584x^{7}+2000x^{6}+240x^{5}-776x^{4}+304x^{3}+200x^{2}-56x-23.}$

Потом, Декартовы координаты сфеномегакороны с длиной ребра 2 задаются объединением орбит точек

${\displaystyle (0,1,2{\sqrt {1-k^{2}}}),\,(2k,1,0),\,\left(0,{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}}+1,{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),}$

${\displaystyle (1,0,-{\sqrt {2+4k-4k^{2}}}),\,\left(0,{\frac {{\sqrt {3-4k^{2}}}(2k^{2}-1)}{(k^{2}-1){\sqrt {1-k^{2}}}}}+1,{\frac {2k^{4}-1}{(1-k^{2})^{\frac {3}{2}}}}\right)}$

под действием группа генерируется отражениями относительно плоскости xz и плоскости yz.^[2]

Затем мы можем вычислить площадь поверхности клиновидной короны реберной длины а в качестве

${\displaystyle A=(2+4{\sqrt {3}})a^{2}\approx 8.92820a^{2},}$^[3]

и это объем в качестве

${\displaystyle V=\xi a^{3}\approx 1.94811a^{3},}$

где десятичное разложение ξ дан кем-то A334114.^[4]

Рекомендации

1. Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский математический журнал, 18: 169–200, Дои:10.4153 / cjm-1966-021-8, МИСТЕР  0185507, Zbl  0132.14603.
2. Тимофеенко, А. В. (2009). «Неплатоновы и неархимедовы несоставные многогранники». Журнал математических наук. 162 (5): 720.
3. Wolfram Research, Inc. (2020). "Wolfram | Alpha Knowledgebase". Шампейн, Иллинойс. PolyhedronData [{"Johnson", 88}, "SurfaceArea"]
4. OEIS Foundation Inc. (2020), Интернет-энциклопедия целочисленных последовательностей, A334114.

внешняя ссылка

• Эрик В. Вайсштейн, Sphenomegacorona (Джонсон солид ) в MathWorld.