Курносый (геометрия) - Snub (geometry)

Эти два пренебрежительно Архимедовы тела

Курносый куб или же Курносый кубооктаэдр

Курносый додекаэдр или же Курносый икосододекаэдр

Две хиральные копии курносого куба в виде чередующихся (красных или зеленых) вершин усеченного кубооктаэдра.

А курносый куб может быть построен из ромбокубооктаэдр повернув 6 синих квадратных граней, пока 12 белых квадратных граней не станут парами равносторонних треугольных граней.

В геометрия, а пренебрежительно - операция над многогранником. Термин происходит от Кеплер Имена двух Архимедовы тела, для курносый куб (cubus simus) и курносый додекаэдр (додекаэдрон симум).^[1] Обычно курносые имеют киральную симметрию двух форм: с ориентацией по часовой стрелке или против часовой стрелки. По именам Кеплера пренебрежительное отношение можно рассматривать как расширение правильного многогранника: раздвигая грани, скручивая их вокруг их центров, добавляя новые многоугольники с центрами на исходных вершинах, и добавляя пары треугольников, подходящих между исходными ребрами.

Терминология была обобщена Coxeter, с немного другим определением, для более широкого набора однородные многогранники.

Конвей пренебрежительно

Джон Конвей исследовали обобщенные операторы многогранников, определяя то, что теперь называется Обозначения многогранника Конвея, который можно применить к многогранникам и мозаикам. Конвей называет операцию Кокстера полуросый.^[2]

В этих обозначениях пренебрежительно определяется двойственным и гироскоп операторы, как s = dg, и это эквивалентно чередование усечения амвон оператор. Сама нотация Конвея избегает операции чередования (половины) Кокстера, поскольку она применима только к многогранникам только с четными гранями.

Сглаженные обычные фигуры

Формы пренебречь	Многогранники			Евклидовы мозаики		Гиперболические мозаики
Имена	Тетраэдр	Куб или же октаэдр	Икосаэдр или же додекаэдр	Квадратная плитка	Шестиугольная черепица или же Треугольная черепица	Семиугольная черепица или же Треугольная черепица Order-7
Изображений
Курносая форма Конвей обозначение	СТ	sC = sO	sI = sD	sQ	sH = sΔ	sΔ7
Изображение

В четырех измерениях Конвей предлагает курносый 24-элементный следует называть полу-курносый 24-элементный потому что, в отличие от 3-мерных курносых многогранников, это чередующиеся всеусеченные формы, это не чередование комплексно усеченные 24 ячейки. Вместо этого на самом деле это альтернативный усеченный 24-элементный.^[3]

Курносые Кокстера, регулярные и квазирегулярные

Курносый куб, образованный из куба или кубооктаэдра

	Семя	Исправленный р	Усеченный т	Альтернативный час
Имя	Куб	Кубооктаэдр Ректифицированный куб	Усеченный кубооктаэдр Усеченный куб	Курносый кубооктаэдр Плоский ректификованный куб
Обозначение Конвея	C	CO rC	тСО trC или trO	htCO = sCO htrC = srC
Символ Шлефли	{4,3}	${displaystyle {egin{Bmatrix}43end{Bmatrix}}}$ или г {4,3}	${displaystyle t{egin{Bmatrix}43end{Bmatrix}}}$ или tr {4,3}	${displaystyle ht{egin{Bmatrix}43end{Bmatrix}}=s{egin{Bmatrix}43end{Bmatrix}}}$ htr {4,3} = sr {4,3}
Диаграмма Кокстера		или же	или же	или же
Изображение

Coxeter терминология пренебрежения немного отличается, что означает чередовались усечение, выводя курносый куб как пренебрежительно кубооктаэдр, а курносый додекаэдр как пренебрежительно икосододекаэдр. Это определение используется для обозначения двух Твердые тела Джонсона: the курносый дисфеноид и курносая квадратная антипризма, и многогранников более высокой размерности, таких как 4-мерный курносый 24-элементный, с расширенным символом Шлефли s {3,4,3} и диаграммой Кокстера .

А правильный многогранник (или мозаика), с символом Шлефли ${displaystyle {egin{Bmatrix}p,qend{Bmatrix}}}$, и Диаграмма Кокстера , имеет усечение определяется как ${displaystyle t{egin{Bmatrix}p,qend{Bmatrix}}}$, и , а пренебрежительное определение - чередовались усечение ${displaystyle ht{egin{Bmatrix}p,qend{Bmatrix}}=s{egin{Bmatrix}p,qend{Bmatrix}}}$, и . Эта альтернативная конструкция требует q быть даже.

А квазирегулярный многогранник, с символом Шлефли ${displaystyle {egin{Bmatrix}pqend{Bmatrix}}}$ или же р{п,q} и диаграмма Кокстера или же , имеет квазирегулярный усечение определяется как ${displaystyle t{egin{Bmatrix}pqend{Bmatrix}}}$ или же tr{п,q}, и или же , и имеет квазирегулярный курносый, определяемый как чередовались усеченное выпрямление ${displaystyle ht{egin{Bmatrix}pqend{Bmatrix}}=s{egin{Bmatrix}pqend{Bmatrix}}}$ или же htr{п,q} = SR{п,q}, и или же .

Например, Кеплер курносый куб выводится из квазирегулярного кубооктаэдр, с вертикальной Символ Шлефли ${displaystyle {egin{Bmatrix}43end{Bmatrix}}}$, и Диаграмма Кокстера , и поэтому более явно называется курносый кубооктаэдр, выраженный вертикальным символом Шлефли ${displaystyle s{egin{Bmatrix}43end{Bmatrix}}}$, и диаграмма Кокстера . Курносый кубооктаэдр - это чередование усеченный кубооктаэдр, ${displaystyle t{egin{Bmatrix}43end{Bmatrix}}}$, и .

Правильные многогранники с вершинами четного порядка также можно игнорировать как чередующиеся усечения, например курносый октаэдр, в качестве ${displaystyle s{egin{Bmatrix}3,4end{Bmatrix}}}$, , является чередованием усеченный октаэдр, ${displaystyle t{egin{Bmatrix}3,4end{Bmatrix}}}$, и . В курносый октаэдр представляет псевдоикосаэдр, обычный икосаэдр с пиритоэдрическая симметрия.

В курносый тетратетраэдр, в качестве ${displaystyle s{egin{Bmatrix}33end{Bmatrix}}}$, и , - чередование усеченной тетраэдрической формы симметрии, ${displaystyle t{egin{Bmatrix}33end{Bmatrix}}}$, и .

	Семя	Усеченный т	Альтернативный час
Имя	Октаэдр	Усеченный октаэдр	Курносый октаэдр
Обозначение Конвея	О	к	htO или sO
Символ Шлефли	{3,4}	т {3,4}	ht {3,4} = s {3,4}
Диаграмма Кокстера
Изображение

Курносливая операция Кокстера также позволяет не-антипризмы быть определенным как ${displaystyle s{egin{Bmatrix}2 end{Bmatrix}}}$ или же ${displaystyle s{egin{Bmatrix}2,2nend{Bmatrix}}}$, на основе n-призм ${displaystyle t{egin{Bmatrix}2 end{Bmatrix}}}$ или же ${displaystyle t{egin{Bmatrix}2,2nend{Bmatrix}}}$, пока ${displaystyle {egin{Bmatrix}2,nend{Bmatrix}}}$ является регулярным n-осоэдр, вырожденный многогранник, но действительный замощение на сфере с Digon или же луна -образные лица.

Курносый Hosohedra, {2,2p}

Изображение
Coxeter диаграммы							... ...
Schläfli символы	с {2,4}	с {2,6}	с {2,8}	с {2,10}	с {2,12}	с {2,14}	с {2,16}...	s {2, ∞}
	ср {2,2} ${displaystyle s{egin{Bmatrix}22end{Bmatrix}}}$	ср {2,3} ${displaystyle s{egin{Bmatrix}23end{Bmatrix}}}$	sr {2,4} ${displaystyle s{egin{Bmatrix}24end{Bmatrix}}}$	ср {2,5} ${displaystyle s{egin{Bmatrix}25end{Bmatrix}}}$	ср {2,6} ${displaystyle s{egin{Bmatrix}26end{Bmatrix}}}$	ср {2,7} ${displaystyle s{egin{Bmatrix}27end{Bmatrix}}}$	ср {2,8} ... ${displaystyle s{egin{Bmatrix}28end{Bmatrix}}}$...	sr {2, ∞} ${displaystyle s{egin{Bmatrix}2infty end{Bmatrix}}}$
Конвей обозначение	A2 = T	A3 = O	A4	A5	A6	A7	A8 ...	A∞

Тот же самый процесс применяется к укороченным плиткам:

Треугольная черепица Δ	Усеченный треугольная черепица tΔ	Плоская треугольная черепица htΔ = sΔ
{3,6}	т {3,6}	ht {3,6} = s {3,6}

Примеры

Оскорбления на основе {p, 4}

Космос	Сферический		Евклидово	Гиперболический
Изображение
Coxeter диаграмма								...
Schläfli символ	с {2,4}	с {3,4}	с {4,4}	с {5,4}	с {6,4}	с {7,4}	с {8,4}	...s {∞, 4}

Квазирегулярные пренебрежения на основе r {p, 3}

Конвей обозначение	Сферический				Евклидово	Гиперболический
Изображение
Coxeter диаграмма								...
Schläfli символ	ср {2,3}	ср {3,3}	sr {4,3}	ср {5,3}	sr {6,3}	sr {7,3}	ср {8,3}	...sr {∞, 3}
	${displaystyle s{egin{Bmatrix}23end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}33end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}43end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}53end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}63end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}73end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}83end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}infty 3end{Bmatrix}}}$
Конвей обозначение	A3	СТ	sC или sO	sD или sI	sΗ или sΔ

Квазирегулярные пренебрежения на основе r {p, 4}

Космос	Сферический		Евклидово	Гиперболический
Изображение
Coxeter диаграмма								...
Schläfli символ	sr {2,4}	sr {3,4}	sr {4,4}	sr {5,4}	sr {6,4}	sr {7,4}	sr {8,4}	...sr {∞, 4}
	${displaystyle s{egin{Bmatrix}24end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}34end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}44end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}54end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}64end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}74end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}84end{Bmatrix}}}$	${displaystyle s{egin{Bmatrix}infty 4end{Bmatrix}}}$
Конвей обозначение	A4	sC или sO	sQ

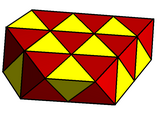
Неоднородные курносые многогранники

Неравномерные многогранники со всеми четными вершинами могут быть пренебрежительными, включая некоторые бесконечные множества; Например:

Курносые бипирамиды sdt {2, p}

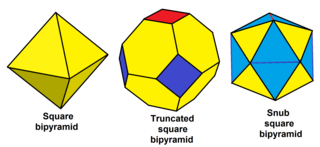Курносая квадратная бипирамида
Курносая шестиугольная бипирамида

Курносые ректифицированные бипирамиды srdt {2, p}

Курносые антипризмы s {2,2p}

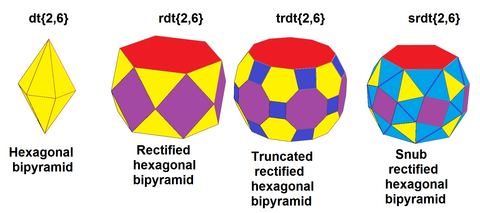Изображение				...
Schläfli символы	сс {2,4}	сс {2,6}	сс {2,8}	сс {2,10} ...
	ssr {2,2} ${displaystyle ss{egin{Bmatrix}22end{Bmatrix}}}$	ssr {2,3} ${displaystyle ss{egin{Bmatrix}23end{Bmatrix}}}$	ssr {2,4} ${displaystyle ss{egin{Bmatrix}24end{Bmatrix}}}$	ssr {2,5} ... ${displaystyle ss{egin{Bmatrix}25end{Bmatrix}}}$

Однородные курносые звездные многогранники Кокстера

Курносые звездные многогранники строятся по их Треугольник Шварца (p q r), с рациональными упорядоченными углами зеркал, и все зеркала активны и чередуются.

Принесенные однородные звездчатые многогранники

с {3 / 2,3 / 2}	с {(3,3,5 / 2)}	ср {5,5 / 2}	с {(3,5,5 / 3)}	ср {5 / 2,3}
ср {5 / 3,5}	s {(5 / 2,5 / 3,3)}	ср {5 / 3,3}	s {(3 / 2,3 / 2,5 / 2)}	с {3 / 2,5 / 3}

Курносые многогранники и соты Кокстера многомерные

В целом регулярный полихорон с Символ Шлефли ${displaystyle {egin{Bmatrix}p,q,rend{Bmatrix}}}$, и Диаграмма Кокстера пренебрегает расширенный символ Шлефли ${displaystyle s{egin{Bmatrix}p,q,rend{Bmatrix}}}$, и .

Ректифицированный полихорон ${displaystyle {egin{Bmatrix}pq,rend{Bmatrix}}}$ = г {р, д, г}, и имеет пренебрежительный символ ${displaystyle s{egin{Bmatrix}pq,rend{Bmatrix}}}$ = sr {p, q, r}, и .

Примеры

Ортогональная проекция курносый 24-элементный

В 4-х измерениях есть только один равномерный выпуклый курносый, курносый 24-элементный. Регулярный 24-элементный имеет Символ Шлефли, ${displaystyle {egin{Bmatrix}3,4,3end{Bmatrix}}}$, и Диаграмма Кокстера , а курносый 24-элементный ${displaystyle s{egin{Bmatrix}3,4,3end{Bmatrix}}}$, Диаграмма Кокстера . Он также имеет конструкцию более низкой симметрии индекса 6 как ${displaystyle sleft{{egin{array}{l}333end{array}}ight}}$ или s {3^1,1,1} и , а подсимметрию индекса 3 как ${displaystyle s{egin{Bmatrix}33,4end{Bmatrix}}}$ или sr {3,3,4}, и или же .

Связанные курносый 24-элементный сотовый можно рассматривать как ${displaystyle s{egin{Bmatrix}3,4,3,3end{Bmatrix}}}$ или s {3,4,3,3}, и , и более низкая симметрия ${displaystyle s{egin{Bmatrix}33,4,3end{Bmatrix}}}$ или sr {3,3,4,3} и или же , а низшая симметрия имеет вид ${displaystyle sleft{{egin{array}{l}3333end{array}}ight}}$ или s {3^1,1,1,1} и .

Евклидовы соты - это чередующиеся шестиугольные плиты сотовой структуры, s {2,6,3} и или sr {2,3,6}, и или sr {2,3^[3]}, и .

Еще одна евклидова (чешуйчатая) соты - это ячеистая плита с чередованием квадратных плит, s {2,4,4} и или sr {2,4^1,1} и :

Единственные однородные курносые гиперболические однородные соты - это плоские шестиугольные черепичные соты, как s {3,6,3} и , который также можно построить как чередующиеся шестиугольные черепичные соты, ч {6,3,3}, . Он также построен как s {3^[3,3]} и .

Другой гиперболический (чешуйчатый) сот - это четырехгранные соты с четырехгранной структурой, s {3,4,4} и .

Смотрите также

• Курносый многогранник

Операторы многогранников

[

• v
• т
• е

]

Семя	Усечение	Исправление	Bitruncation	Двойной	Расширение	Омнитуркация	Чередования
т0{p, q} {p, q}	т01{p, q} т {р, д}	т1{p, q} г {р, д}	т12{p, q} 2t {p, q}	т2{p, q} 2r {p, q}	т02{p, q} рр {р, q}	т012{p, q} tr {p, q}	ht0{p, q} ч {д, р}	ht12{p, q} s {q, p}	ht012{p, q} sr {p, q}

Рекомендации

1. Кеплер, Harmonices Mundi, 1619
2. Конвей, (2008) стр.287 Операция полу-курносого Кокстера
3. Конвей, 2008, стр. 401 Полупурносый полиоктаэдр Госсета.

• Кокстер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки.. Королевское общество. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. Дои:10.1098 / рста.1954.0003. ISSN  0080-4614. JSTOR  91532. МИСТЕР  0062446.
• Кокстер, H.S.M. Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN  0-486-61480-8 (стр. 154–156. 8.6 Частичное усечение или чередование)
• Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN  978-0-471-01003-6 [1], Googlebooks [2]
  • (Документ 17) Coxeter, Эволюция диаграмм Кокстера – Дынкина., [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
  • (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559–591]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3–45]
• Coxeter, Красота геометрии: двенадцать эссе, Dover Publications, 1999 г., ISBN  978-0-486-40919-1 (Глава 3: Конструкция Витхоффа для однородных многогранников)
• Норман Джонсон Равномерные многогранники, Рукопись (1991)
  • N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
• Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN  978-1-56881-220-5
• Вайсштейн, Эрик В. «Оскорбление». MathWorld.
• Ричард Клитцинг, Плоскогубцы, чередующиеся фасетки и диаграммы Стотта – Кокстера – Дынкина., Симметрия: культура и наука, Vol. 21, №4, 329–344, (2010) [3]