Курносый многогранник - Snub polyhedron
| Многогранник | |
| Учебный класс | Количество и свойства |
|---|---|
| Платоновы тела | (5, выпуклый, правильный) |
| Архимедовы тела | (13, выпуклый, равномерный) |
| Многогранники Кеплера – Пуансо | (4, правильная, невыпуклая) |
| Равномерные многогранники | (75, униформа) |
| Призматоид: призмы, антипризмы и Т. Д. | (4 бесконечные однородные классы) |
| Многогранники мозаики | (11 обычных, в плоскости) |
| Квазиправильные многогранники | (8) |
| Твердые тела Джонсона | (92, выпуклая, неравномерная) |
| Пирамиды и Бипирамиды | (бесконечный) |
| Звёздчатые | Звёздчатые |
| Многогранные соединения | (5 обычных) |
| Дельтаэдра | (Дельтаэдра, равносторонние треугольные грани) |
| Курносые многогранники | (12 униформа, а не зеркальное отображение) |
| Зоноэдр | (Зоноэдры, грани имеют симметрию 180 °) |
| Двойной многогранник | |
| Самодвойственный многогранник | (бесконечный) |
| Каталонский твердый | (13, Архимедово дуальное) |
А пренебрежительно многогранник это многогранник получено чередование соответствующий всесторонне усеченный или же усеченный многогранник, в зависимости от определения. Некоторые, но не все авторы включают антипризмы в качестве курносых многогранников, поскольку они получаются с помощью этой конструкции из вырожденного "многогранника" только с двумя гранями (a диэдр ).
Хиральный курносые многогранники не всегда имеют симметрия отражения и поэтому иногда бывает два энантиоморфный формы, которые являются отражением друг друга. Их группы симметрии все точечные группы.
Например, курносый куб:
 |  |
Курносые многогранники имеют Символ Wythoff | p q r и, соответственно, конфигурация вершины 3.п.3.q.3.р. Многогранники Retrosnub (подмножество курносых многогранников, содержащие большой икосаэдр, малый ретроснуб икосикосододекаэдр, и большой ретроснуб икосододекаэдр ) все еще имеют эту форму символа Wythoff, но их конфигурации вершин вместо этого (3.−p.3.−q.3.−r)/2.
Список курносых многогранников
Униформа
Имеется 12 однородных курносых многогранников, не считая антипризм, икосаэдр как пренебрежение тетраэдр, то большой икосаэдр как ретроснуб тетраэдр и большой дизнуб диргомбидодекаэдр, также известный как Фигура Скиллинга.
Когда Треугольник Шварца курносого многогранника равнобедренный курносый многогранник не является киральным. Так обстоит дело с антипризмами, икосаэдр, то большой икосаэдр, то малый курносый икосикосододекаэдр, а малый ретроснуб икосикосододекаэдр.
На изображениях, являющихся производными курносых (демонстрирующих искаженный курносый многогранник, топологически идентичный однородной версии, полученный в результате геометрического чередования родительского однородного всесторонне усеченного многогранника), где зеленый цвет отсутствует, грани, полученные в результате чередования, окрашены в красный и желтый цвета, в то время как курносые треугольники синие. Где присутствует зеленый цвет (только для курносый икосододекадодекаэдр и большой курносый додецикосододекаэдр ), грани, полученные в результате чередования, - красный, желтый и синий, а курносые треугольники - зеленые.
| Курносый многогранник | Изображение | Оригинальный всесторонне усеченный многогранник | Изображение | Курносый вывод | Группа симметрии | Символ Wythoff Описание вершины |
|---|---|---|---|---|---|---|
| Икосаэдр (курносый тетраэдр) |  | Усеченный октаэдр |  | 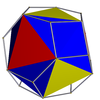 | ячас (Тчас) | | 3 3 2 3.3.3.3.3 |
| Большой икосаэдр (ретроснуб тетраэдр) |  | Усеченный октаэдр |  | 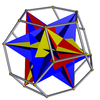 | ячас (Тчас) | | 2 3/2 3/2 (3.3.3.3.3)/2 |
| Курносый куб или курносый кубооктаэдр |  | Усеченный кубооктаэдр |  | 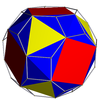 | О | | 4 3 2 3.3.3.3.4 |
| Курносый додекаэдр или курносый икосододекаэдр |  | Усеченный икосододекаэдр |  |  | я | | 5 3 2 3.3.3.3.5 |
| Малый курносый икосикосододекаэдр |  | Дважды покрытый усеченный икосаэдр |  |  | ячас | | 3 3 5/2 3.3.3.3.3.5/2 |
| Курносый додекадодекаэдр |  | Малый ромбидодекаэдр с дополнительными 12 {10/2} лица |  |  | я | | 5 5/2 2 3.3.5/2.3.5 |
| Курносый икосододекадодекаэдр |  | Икоситроусеченный додекадодекаэдр |  | 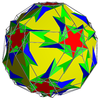 | я | | 5 3 5/3 3.5/3.3.3.3.5 |
| Большой курносый икосододекаэдр |  | Ромбикосаэдр с дополнительными 12 {10/2} лица |  |  | я | | 3 5/2 2 3.3.5/2.3.3 |
| Перевернутый курносый додекадодекаэдр |  | Усеченный додекадодекаэдр |  |  | я | | 5 2 5/3 3.5/3.3.3.3.5 |
| Большой курносый додецикосододекаэдр |  | Большой додецикосаэдр с дополнительными 12 {10/2} лица |  | еще нет изображения | я | | 3 5/2 5/3 3.5/3.3.5/2.3.3 |
| Большой перевернутый курносый икосододекаэдр |  | Большой усеченный икосододекаэдр |  |  | я | | 3 2 5/3 3.5/3.3.3.3 |
| Малый ретроснуб икосикосододекаэдр |  | Дважды покрытый усеченный икосаэдр |  | еще нет изображения | ячас | | 5/2 3/2 3/2 (3.3.3.3.3.5/2)/2 |
| Большой ретроснуб икосододекаэдр |  | Большой ромбидодекаэдр с дополнительными 20 {6/2} лица |  | еще нет изображения | я | | 2 5/3 3/2 (3.3.3.5/2.3)/2 |
| Большой диромбикосододекаэдр |  | — | — | — | ячас | | 3/2 5/3 3 5/2 (4.3/2.4.5/3.4.3.4.5/2)/2 |
| Большой дизнуб диргомбидодекаэдр |  | — | — | — | ячас | | (3/2) 5/3 (3) 5/2 (3/2.3/2.3/2.4.5/3.4.3.3.3.4.5/2.4)/2 |
Примечания:
- В икосаэдр, курносый куб и курносый додекаэдр единственные трое выпуклый ед. Они получаются пренебрежением усеченный октаэдр, усеченный кубооктаэдр и усеченный икосододекаэдр - три выпуклых усеченных квазирегулярные многогранники.
- Единственный курносый многогранник с хиральный октаэдрическая группа симметрии курносый куб.
- Только икосаэдр и большой икосаэдр являются также правильные многогранники. Они также дельтаэдры.
- Только икосаэдр, большой икосаэдр, малый курносый икосикосододекаэдр, малый ретроснуб икосикосододекаэдр, большой диромбикосододекаэдр, и большой дизнуб диргомбидодекаэдр также обладают отражающей симметрией.
Также существует бесконечный набор антипризмы. Они сформированы из призмы, которые усечены Hosohedra, выродиться правильные многогранники. Те, что до шестиугольника, перечислены ниже. На рисунках, показывающих возникновение курноса, грани, полученные в результате чередования (оснований призм), окрашены в красный цвет, а курносые треугольники окрашены в желтый цвет. Исключением является тетраэдр, у которого все грани образованы как красные курносые треугольники, поскольку чередование квадратных оснований куба приводит к вырождению. дигоны как лица.
| Курносый многогранник | Изображение | Исходный всесторонне усеченный многогранник | Изображение | Курносый вывод | Группа симметрии | Символ Wythoff Описание вершины |
|---|---|---|---|---|---|---|
| Тетраэдр |  | Куб | 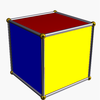 |  | Тd (D2d) | | 2 2 2 3.3.3 |
| Октаэдр |  | Гексагональная призма | 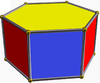 | 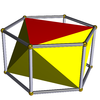 | Очас (D3D) | | 3 2 2 3.3.3.3 |
| Квадратная антипризма |  | Восьмиугольная призма |  | 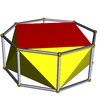 | D4d | | 4 2 2 3.4.3.3 |
| Пятиугольная антипризма |  | Десятиугольная призма |  | 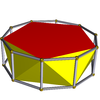 | D5d | | 5 2 2 3.5.3.3 |
| Пентаграммическая антипризма |  | Дважды покрытый пятиугольная призма |  |  | D5ч | | 5/2 2 2 3.5/2.3.3 |
| Пентаграмматическая скрещенная антипризма |  | Декаграммическая призма |  | 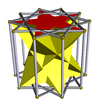 | D5d | | 2 2 5/3 3.5/3.3.3 |
| Шестиугольная антипризма |  | Додекагональная призма | 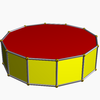 | 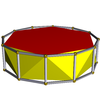 | D6d | | 6 2 2 3.6.3.3 |
Примечания:
- Два из этих многогранников могут быть построены из первых двух курносых многогранников в списке, начиная с икосаэдр: the пятиугольная антипризма это парабидоусиленный икосаэдр и пентаграмматическая скрещенная антипризма парабидоусиленный большой икосаэдр, также известный как парабиэдр большой икосаэдр.
Неоднородный
Два Твердые тела Джонсона курносые многогранники: курносый дисфеноид и курносая квадратная антипризма. Ни то, ни другое не является хиральным.
| Курносый многогранник | Изображение | Исходный многогранник | Изображение | Группа симметрии |
|---|---|---|---|---|
| Курносый дисфеноид |  | Дисфеноид |  | D2d |
| Плоская квадратная антипризма |  | Квадратная антипризма |  | D4d |
Рекомендации
- Кокстер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 246 (916): 401–450, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446, S2CID 202575183
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.
- Скиллинг, Дж. (1975), "Полный набор однородных многогранников", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 278 (1278): 111–135, Дои:10.1098 / рста.1975.0022, ISSN 0080-4614, JSTOR 74475, МИСТЕР 0365333, S2CID 122634260
- Мэдер, Р. Э. Однородные многогранники. Mathematica J. 3, 48-57, 1993.
| Семя | Усечение | Исправление | Bitruncation | Двойной | Расширение | Омнитуркация | Чередования | ||
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  | |||||
| т0{p, q} {p, q} | т01{p, q} т {р, д} | т1{p, q} г {р, д} | т12{p, q} 2t {p, q} | т2{p, q} 2r {p, q} | т02{p, q} рр {р, q} | т012{p, q} tr {p, q} | ht0{p, q} ч {д, р} | ht12{p, q} s {q, p} | ht012{p, q} sr {p, q} |
