Пентаграммическая антипризма - Pentagrammic antiprism
| Униформа пентаграммическая антипризма | |
|---|---|
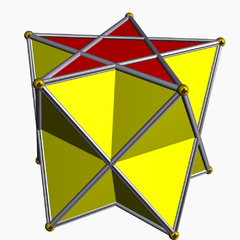 | |
| Тип | Призматический однородный многогранник |
| Элементы | F = 12, E = 20 V = 10 (χ = 2) |
| Лица по сторонам | 10{3}+2{5/2} |
| Символ Шлефли | sr {2,5/2} |
| Символ Wythoff | | 2 2 5/2 |
| Диаграмма Кокстера | |
| Симметрия | D5ч, [5,2], (* 552), порядок 20 |
| Группа вращения | D5, [5,2]+, (55), порядок 10 |
| Указатель ссылок | U79 (а) |
| Двойной | Пентаграмматический трапецоэдр |
| Характеристики | невыпуклый |
 Фигура вершины 3.3.3.5/2 | |

В геометрия, то пентаграммическая антипризма один в бесконечном множестве невыпуклых антипризмы образованный сторонами треугольника и двумя правильными звездный многоугольник колпачки, в данном случае два пентаграммы.
У него 12 граней, 20 ребер и 10 вершин. Этот многогранник обозначается индексированным именем U79 как равномерный многогранник[1].
Обратите внимание, что лицо пентаграммы имеет неоднозначный интерьер, потому что оно самопересекающееся. Центральную область пятиугольника можно рассматривать как внутреннюю или внешнюю, в зависимости от того, как определяется интерьер. Одно определение интерьера - это набор точек, луч которых пересекает границу нечетное число раз, чтобы выйти за периметр.
В любом случае лучше всего показать линию границы пентаграммы, чтобы отличить ее от вогнутого десятиугольника.
Галерея
 Альтернативное представление с полыми центрами пентаграмм. Альтернативное представление с полыми центрами пентаграмм. |  В пентаграмма трапецоэдр это двойной к пентаграмматической антипризме. В пентаграмма трапецоэдр это двойной к пентаграмматической антипризме. |
Сеть
Сеть (сложите пунктирную линию по центру в направлении, противоположном всем остальным линиям):
Рекомендации
- ^ Медер, Роман. "79: пентаграммическая антипризма".
Смотрите также
- Призматический однородный многогранник
- Пентаграммическая призма
- Пентаграмматическая скрещенная антипризма
внешняя ссылка
- Вайсштейн, Эрик В. «Пентаграммическая антипризма». MathWorld.
- http://www.mathconsult.ch/showroom/unipoly/04.html
- https://web.archive.org/web/20050313233653/http://www.math.technion.ac.il/~rl/kaleido/data/04.html
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
