Обычная сетка - Regular grid
Эта статья нужны дополнительные цитаты для проверка. (Декабрь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

А регулярная сетка это мозаика из п-размерный Евклидово пространство к конгруэнтный параллелоэдры (например. кирпичи ).[1] Сетки этого типа появляются на миллиметровая бумага и может использоваться в анализ методом конечных элементов, методы конечных объемов, методы конечных разностей, и вообще для дискретизации пространств параметров. Поскольку производные переменных поля удобно выразить в конечных разностях,[2] Структурированные сетки в основном появляются в методах конечных разностей. Неструктурированные сети предлагают большую гибкость, чем структурированные сетки, и поэтому очень полезны в методах конечных элементов и конечных объемов.
Каждая ячейка в сетке может быть адресована по индексу (i, j) в двух размеры или (i, j, k) в трех измерениях, и каждый вершина имеет координаты в 2D или в 3D для некоторых реальных чисел dx, dy, и дз представляющий шаг сетки.
Связанные сетки
А Декартова сетка это частный случай, когда элементы единичные квадраты или же единичные кубы, а вершины точки на целочисленная решетка.
А прямолинейная сетка тесселяция прямоугольники или же прямоугольные кубоиды (также известный как прямоугольные параллелепипеды ), которые, в общем, не все конгруэнтный друг другу. Ячейки по-прежнему могут быть индексированы целыми числами, как указано выше, но отображение индексов в координаты вершин менее равномерное, чем в обычной сетке. Пример нерегулярной прямолинейной сетки появляется на логарифмическая шкала миллиметровая бумага.
А перекошенная сетка представляет собой мозаику параллелограммы или же параллелепипеды. (Если все единицы длины равны, это тесселяция ромбовидные или же ромбоэдры.)
А криволинейная сетка или же структурированная сетка представляет собой сетку с той же комбинаторной структурой, что и регулярная сетка, в которой ячейки четырехугольники или же [общие] кубоиды, а не прямоугольники или прямоугольные кубоиды.
- Примеры регулярных сеток

3-D декартова сетка

Трехмерная прямолинейная сетка
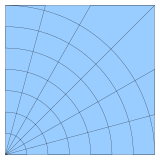
2-мерная криволинейная сетка

2-мерная криволинейная сетка
Смотрите также
Рекомендации
- ^ Узнанский, Дан. "Сетка". Из MathWorld - веб-ресурса Wolfram, созданного Эриком Вайсштейном. Получено 25 марта 2012.
- ^ Дж. Ф. Томпсон, Б. К. Soni & N.P. Weatherill (1998). Справочник по созданию сети. CRC-Press. ISBN 978-0-8493-2687-5.
| Этот Связанные с элементарной геометрией статья - это заглушка. Вы можете помочь Википедии расширяя это. |








