Додекагон - Dodecagon

Правильный двенадцатигранник
Правильный двенадцатигранник
Тип	Правильный многоугольник
Края и вершины	12
Символ Шлефли	{12}, т {6}, тт {3}
Диаграмма Кокстера
Группа симметрии	Двугранный (D12), порядок 2 × 12
Внутренний угол (градусы )	150°
Двойной многоугольник	Себя
Характеристики	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрия, а двенадцатигранник или 12-угольник - это любой двенадцатигранный многоугольник.

Правильный двенадцатигранник

А обычный Додекагон - это фигура со сторонами одинаковой длины и одинаковыми внутренними углами. Он имеет двенадцать линий отражательной симметрии и вращательной симметрии 12-го порядка. Правильный двенадцатигранник представлен символом Символ Шлефли {12} и может быть выполнен в виде усеченный шестиугольник, t {6}, или дважды усеченный треугольник, тт {3}. Внутренний угол в каждой вершине правильного двенадцатиугольника составляет 150 °.

Площадь

В площадь правильного двенадцатиугольника длины стороны а дан кем-то:

${\displaystyle {\begin{aligned}A&=3\cot \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\simeq 11.19615242\,a^{2}\end{aligned}}}$

А с точки зрения апофема р (смотрите также вписанная фигура ), площадь составляет:

${\displaystyle {\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\simeq 3.2153903\,r^{2}\end{aligned}}}$

Что касается по окружности р, площадь:^[1]

${\displaystyle A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}}$

Размах S двенадцатиугольника - это расстояние между двумя параллельными сторонами, равное удвоенной апофемой. Простая формула для определения площади (с учетом длины стороны и размаха):

${\displaystyle A=3aS}$

Это можно проверить с помощью тригонометрического соотношения:

${\displaystyle S=a(1+2\cos {30^{\circ }}+2\cos {60^{\circ }})}$

Периметр

В периметр правильного двенадцатиугольника по радиусу описанной окружности составляет:^[2]

${\displaystyle {\begin{aligned}p&=24R\tan \left({\frac {\pi }{12}}\right)=12R{\sqrt {2-{\sqrt {3}}}}\\&\simeq 6.21165708246\,R\end{aligned}}}$

Периметр в терминах апофемы:

${\displaystyle {\begin{aligned}p&=24r\tan \left({\frac {\pi }{12}}\right)=24r(2-{\sqrt {3}})\\&\simeq 6.43078061835\,r\end{aligned}}}$

Этот коэффициент вдвое больше коэффициента, найденного в уравнении апофемы для площади.^[3]

Додекагон конструкция

Поскольку 12 = 2² × 3 правильный двенадцатигранник равен конструктивный с помощью компас и линейка:

Построение правильного двенадцатиугольника при заданном описанный круг

Построение правильного двенадцатиугольника
при заданной длине стороны, анимация. (Конструкция очень похожа на восьмиугольник с заданной длиной стороны.)

Рассечение

12-куб	60 рассечение ромба

Изотоксальный додекагон

Coxeter заявляет, что каждый зоногон (а 2м-угольник, противоположные стороны которого параллельны и равной длины) можно разрезать на м(м-1) / 2 параллелограмма.^[4]В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для правильный двенадцатигранник, м= 6, и его можно разделить на 15: 3 квадрата, 6 широких ромбов 30 ° и 6 узких ромбов 15 °. Это разложение основано на Многоугольник Петри проекция 6-куб, с 15 из 240 граней. Последовательность OEIS последовательность A006245 определяет количество решений как 908, включая до 12-кратных поворотов и хиральных форм в отражении.

Рассечение на 15 ромбов

6-куб

Один из способов математический манипулятор блоки шаблона используются при создании ряда различных двенадцатиугольников.^[5] Они связаны с ромбическим рассечением, с 3 ромбами 60 °, объединенными в шестиугольники, полушестиугольными трапециями или разделенными на 2 равносторонних треугольника.

Другие вскрытия

Обычный		блоки шаблона

Симметрия

Симметрии правильного двенадцатиугольника, показанные с помощью цветов на ребрах и вершинах. Джон Конвей обозначает эти более низкие симметрии буквой, а порядок симметрии следует за буквой. Он дает d (диагональ) с зеркальными линиями через вершины, п с зеркальными линиями по краям (перпендикулярно), я с зеркальными линиями через вершины и края, и грамм для вращательной симметрии. а1 этикетки не симметричны. Эти более низкие симметрии позволяют степеням свободы определять неправильные додекагоны.^[6]

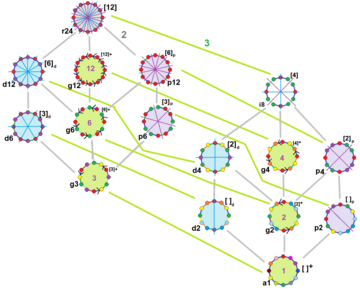
В правильный двенадцатигранник есть Dih₁₂ симметрия, порядок 24. Существует 15 различных подгрупп диэдральных и циклических симметрий. Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только g12 подгруппа не имеет степеней свободы, но может рассматриваться как направленные края.

Пример додекагонов по симметрии
r24
d12	g12	p12		i8
d6	g6	p6		d4	g4	p4
g3				d2	g2	p2
а1

Вхождение

Плитка

Обычный двенадцатигранник может заполнить вершину плоскости с другими правильными многоугольниками 4 способами:

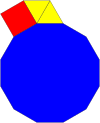3.12.12	4.6.12	3.3.4.12	3.4.3.12

Вот 3 примера периодические плоские мозаики которые используют правильные додекагоны, определяемые их конфигурация вершины:

1-униформа		2-униформа
3.12.12	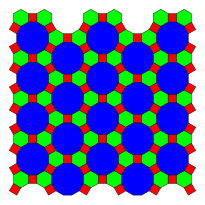4.6.12	3.12.12; 3.4.3.12

Наклонный двенадцатигранник

Правильный косой двенадцатигранник выглядит как зигзагообразные края шестиугольная антипризма.

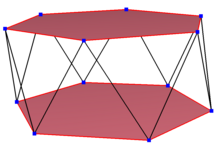
А наклонный двенадцатигранник это наклонный многоугольник с 12 вершинами и ребрами, но не находящихся в одной плоскости. Внутренняя часть такого двенадцатигранника обычно не определяется. А косой зигзагообразный двенадцатигранник имеет чередующиеся вершины между двумя параллельными плоскостями.

А правильный косой двенадцатигранник является вершинно-транзитивный с равной длиной кромки. В 3-х измерениях это будет зигзагообразный косой двенадцатигранник, и его можно будет увидеть в вершинах и боковых краях шестиугольная антипризма с тем же D_5d, [2⁺, 10] симметрия 20-го порядка. додекаграммная антипризма, с {2,24 / 5} и додекаграммная скрещенная антипризма, s {2,24 / 7} также имеют правильные скошенные двенадцатиугольники.

Полигоны Петри

Правильный двенадцатигранник - это Многоугольник Петри для многих многомерных многогранников, рассматриваемых как ортогональные проекции в Самолеты Кокстера. Примеры в 4-х измерениях: 24-элементный, курносый 24-элементный, 6-6 дуопризма, 6-6 дуопирамид. В 6 измерениях 6-куб, 6-ортоплекс, 2₂₁, 1₂₂. Это также многоугольник Петри для большой 120-элементный и большой звездчатый 120-элементный.

Регулярные косые додекагоны в более высоких измерениях
E6		F4		2G2 (4D)
221	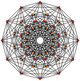122	24-элементный	Курносый 24-элементный	6-6 дуопирамид	6-6 дуопризма
А11	D7		B6
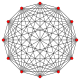11-симплекс	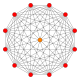(411)	141	6-ортоплекс	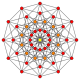6-куб

Связанные цифры

А додекаграмма представляет собой 12-сторонний звездообразный многоугольник, представленный символом {12 / n}. Есть один обычный звездный многоугольник: {12/5}, используя те же вершины, но соединяя каждую пятую точку. Также есть три соединения: {12/2} сокращается до 2 {6} как два шестиугольники, а {12/3} сокращается до 3 {4} как три квадраты, {12/4} уменьшается до 4 {3} как четыре треугольника, а {12/6} уменьшается до 6 {2} как шесть вырожденных дигоны.

Звезды и соединения
п	1	2	3	4	5	6
Форма	Многоугольник	Соединения			Звездный многоугольник	Сложный
Изображение	{12/1} = {12}	{12/2} или 2 {6}	{12/3} или 3 {4}	{12/4} или 4 {3}	{12/5}	{12/6} или 6 {2}

Более глубокие усечения правильного додекагона и додекаграммы могут давать изогональные (вершинно-транзитивный ) образуются промежуточные звёздчатые многоугольники с одинаковыми вершинами и двумя длинами ребер. Усеченный шестиугольник - это двенадцатиугольник, t {6} = {12}. Квазиусеченный шестиугольник, перевернутый как {6/5}, представляет собой додекаграмму: t {6/5} = {12/5}.^[7]

Вершинно-транзитивные усечения шестиугольника
Квазирегулярный	Изогональный		Квазирегулярный
t {6} = {12}			т {6/5} = {12/5}

Примеры в использовании

В блочные капиталы, письма E, ЧАС и Икс (и я в плита с засечками font) имеют двенадцатиугольные очертания. А Пересекать представляет собой двенадцатигранник, как и логотип Chevrolet автомобильное подразделение.

Церковь Вера Крус в Сеговия

Обычный двенадцатигранник занимает видное место во многих зданиях. В Торре дель Оро это двенадцатигранная армия сторожевая башня в Севилья, южный Испания, построенный Династия Альмохадов. Церковь Вера Крус начала XIII века в Сеговия, Испания двенадцатигранная. Другой пример - Порта ди Венере (Ворота Венеры) в Spello, Италия, построенный в I веке до нашей эры, имеет две двенадцатигранных башни, названные «Башнями Проперция».

Британский три пенса 1942 года, реверс

Обычный двенадцатиугольные монеты включают:

• Британский трехпенсовый бит с 1937 по 1971 год, когда он перестал быть законным платежным средством.
• Британская монета в один фунт, представленный в 2017 году.
• 50-центовая австралийская монета
• Фиджийский 50 центов
• Тонга 50-сенити, с 1974 г.
• Соломоновы Острова 50 центов
• Хорватская 25 кун
• Румынский 5000 лей, 2001–2005
• Канадский пенни, 1982–1996
• Южновьетнамский 20 đồng, 1968–1975
• Замбийский 50 нгве, 1969–1992
• Малавийская 50 тамбала, 1986–1995
• Мексиканские 20 сентаво, 1992-2009

в Филиппины, на местных карнавалах (перяханах) колеса обозрения обычно на 12 мест или гондолы.

Смотрите также

• Додекагональное число
• Додекаэдр - обычный многогранник с 12 пятиугольник лица.
• Додекаграмма

Примечания

1. Смотрите также Кюршак геометрическое доказательство на демонстрационный проект Wolfram
2. Плоская геометрия: эксперимент, классификация, открытие, применение Кларенс Аддисон Уиллис Б., (1922) Сын и компания Блэкистона, стр. 249 [1]
3. Элементы геометрии Джона Плейфэра, Уильяма Уоллеса, Джона Дэвидсона, (1814) Bell & Bradfute, стр. 243 [2]
4. Coxeter, Математические развлечения и эссе, тринадцатое издание, с.141
5. "Doin 'Da' Dodeca '" на mathforum.org
6. Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN  978-1-56881-220-5 (Глава 20, Обобщенные символы Шафли, Типы симметрии многоугольника, стр. 275-278)
7. Светлая сторона математики: материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994), Метаморфозы полигонов, Бранко Грюнбаум

внешняя ссылка

• Вайсштейн, Эрик В. «Додекагон». MathWorld.
• Плитка Кюршака и теорема
• Определение и свойства двенадцатиугольника С интерактивной анимацией
• Обычный двенадцатигранник в классе, с помощью блоки шаблона