Триакис икосаэдр - Triakis icosahedron

Триакис икосаэдр
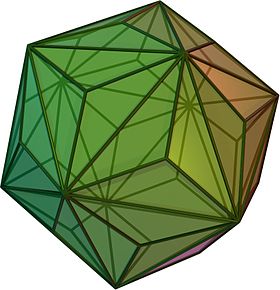(Нажмите здесь, чтобы повернуть модель)
Тип	Каталонский твердый
Диаграмма Кокстера
Обозначение Конвея	kI
Тип лица	V3.10.10 равнобедренный треугольник
Лица	60
Края	90
Вершины	32
Вершины по типу	20{3}+12{10}
Группа симметрии	я_час, H₃, [5,3], (*532)
Группа вращения	Я, [5,3]⁺, (532)
Двугранный угол	160°36′45″ arccos (-24 + 15√5/61)
Характеристики	выпуклый, лицо переходный
Усеченный додекаэдр (двойственный многогранник )	Сеть

3d модель триакиса икосаэдра

В геометрия, то триакис икосаэдр (или же кисикосаэдр^[1]) является Архимедова двойственная твердый, или Каталонский твердый. Его двойным является усеченный додекаэдр.

Декартовы координаты

Позволять ${ displaystyle phi}$ быть Золотое сечение. 12 баллов, присвоенных ${ displaystyle (0, pm 1, pm phi)}$ а циклические перестановки этих координат являются вершинами правильный икосаэдр. Его двойная правильный додекаэдр, чьи ребра пересекают ребра икосаэдра под прямым углом, имеет вершинами точки ${ Displaystyle ( pm 1, pm 1, pm 1)}$ вместе с точками ${ displaystyle ( pm phi, pm 1 / phi, 0)}$ и циклические перестановки этих координат. Умножив все координаты этого додекаэдра на коэффициент ${ Displaystyle (7 фи -1) / 11 приблизительно 0,938 , 748 , 901 , 93}$ дает додекаэдр несколько меньшего размера. 20 вершин этого додекаэдра вместе с вершинами икосаэдра являются вершинами триакисикосаэдра с центром в начале координат. Длина его длинных краев равна ${ displaystyle 2}$ . Его грани представляют собой равнобедренные треугольники с одним тупым углом ${ displaystyle arccos (-3 phi / 10) приблизительно 119,039 , 350 , 869 , 29 ^ { circ}}$ и два острых из ${ displaystyle arccos (( phi +7) / 10) приблизительно 30.480 , 324 , 565 , 36 ^ { circ}}$ . Отношение длин длинных и коротких краев этих треугольников равно ${ displaystyle ( phi +7) / 5 приблизительно 1,723 , 606 , 797 , 75}$ .

Ортогональные проекции

Триакисикосаэдр имеет три положения симметрии: два на вершинах и одно на краю: икосаэдр Триаки имеет пять особых ортогональные проекции с центром на вершине, на двух типах ребер и двух типах граней: шестиугольной и пятиугольной. Последние два соответствуют букве A₂ и H₂ Самолеты Кокстера.

Ортогональные проекции каркасных мод
Проективный симметрия	[2]	[6]	[10]
Изображение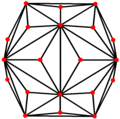
Двойной изображение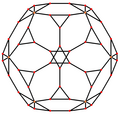

Kleetope

Это можно рассматривать как икосаэдр с треугольные пирамиды дополнено к каждому лицу; то есть это Kleetope икосаэдра. Это толкование выражено в названии, Triakis.

Если икосаэдр дополнить тетраэдром без удаления центрального икосаэдра, получится чистая икосаэдрическая пирамида.

Другие триаки икосаэдры

Эта интерпретация также может применяться к другим подобным невыпуклым многогранникам с пирамидами разной высоты:

Первая звёздчатая форма икосаэдра, или же Малый триамбический икосаэдр, или иногда называемый Триакис икосаэдр (среди прочего)
Большой звездчатый додекаэдр (с очень высокими пирамидами)
Большой додекаэдр (с перевернутыми пирамидами)

Звёздчатые

Триакисикосаэдр имеет множество звёздчатые, включая Вот этот.

Связанные многогранники

Сферический триакис икосаэдр

Семейство однородных икосаэдрических многогранников
Симметрия: [5,3], (*532)							[5,3]⁺, (532)


{5,3}	т {5,3}	г {5,3}	т {3,5}	{3,5}	рр {5,3}	tr {5,3}	ср {5,3}
Двойники к однородным многогранникам

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Триакисикосаэдр является частью последовательности многогранников и мозаик, простирающейся в гиперболическую плоскость. Эти лицо переходный фигуры имеют (* n32) отражающие симметрия.

*п32 мутации симметрии усеченных мозаик: t {п,3} [ v т е ]
Симметрия *п32 [n, 3]	Сферический				Евклид.	Компактная гиперболия.		Paraco.	Некомпактный гиперболический
Симметрия *п32 [n, 3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
Усеченный цифры
Символ	т {2,3}	т {3,3}	т {4,3}	т {5,3}	т {6,3}	т {7,3}	т {8,3}	т {∞, 3}	т {12i, 3}	т {9i, 3}	т {6i, 3}
Triakis цифры
Конфиг.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞