Золотое сечение - Golden ratio

Эта статья про число. Об альбоме Ace of Base см. Золотое сечение (альбом). Для календарных дат см. Золотое число (время).

Отрезки в золотом сечении

А золотой прямоугольник с более длинной стороной а и более короткая сторона б, при размещении рядом с квадратом со сторонами длины а, создаст похожий золотой прямоугольник с длинной стороной а + б и более короткая сторона а. Это иллюстрирует отношения ${displaystyle {frac {a+b}{a}}={frac {a}{b}}equiv varphi }$.

В математика, две величины находятся в Золотое сечение если их соотношение такое же, как и соотношение их сумма к большему из двух величин. Рисунок справа иллюстрирует геометрические отношения. Выражается алгебраически для величин а и б с а > б > 0,

${displaystyle {frac {a+b}{a}}={frac {a}{b}} {stackrel { ext{def}}{=}} varphi ,}$

где греческая буква фи (${displaystyle varphi }$ или же ${displaystyle phi }$) представляет собой золотое сечение.^[1][а] Это иррациональный номер это решение квадратного уравнения ${displaystyle x^{2}-x-1=0}$, со значением:

${displaystyle varphi ={frac {1+{sqrt {5}}}{2}}=1.6180339887ldots .}$^[2][3]

Золотое сечение также называют Золотая середина или же золотое сечение (латинский: sectio aurea).^[4][5] Другие имена включают крайнее и среднее соотношение,^[6] медиальный отдел, божественная пропорция (Латинский: proportio divina),^[7] божественный раздел (Латинский: Sectio Divina), золотая пропорция, золотая огранка,^[8] и золотой номер.^[9][10][11]

Математики поскольку Евклид изучили свойства золотого сечения, в том числе его появление в размерах правильный пятиугольник и в золотом прямоугольнике, который можно разрезать на квадрат и меньший прямоугольник с тем же соотношение сторон. Золотое сечение также использовалось для анализа пропорций природных объектов, а также искусственных систем, таких как финансовые рынки, в некоторых случаях на основании сомнительного соответствия данным.^[12] Золотое сечение появляется в некоторых закономерности в природе, в том числе спиральное расположение листьев и другие части растений.

Некоторые двадцатого века художники и архитекторы, включая Ле Корбюзье и Сальвадор Дали, распределили свои работы так, чтобы приблизиться к золотому сечению, полагая, что это эстетически приятно. Они часто появляются в виде золотой прямоугольник, в котором отношение длинной стороны к короткой является золотым сечением.

Расчет

Список номеров Иррациональные числа ζ(3) √2 √3 √5 φ е π
Двоичный	1.1001111000110111011...
Десятичный	1.6180339887498948482...[3]
Шестнадцатеричный	1.9E3779B97F4A7C15F39 ...
Непрерывная дробь	${displaystyle 1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}}}}$
Алгебраическая форма	${displaystyle {frac {1+{sqrt {5}}}{2}}}$

Греческая буква фи символизирует золотое сечение. Обычно строчная форма (φ или φ) используется. Иногда форма верхнего регистра (${displaystyle Phi }$) используется для взаимный золотого сечения, 1 /φ.^[13]

Две величины а и б говорят, что находятся в Золотое сечение φ если

${displaystyle {frac {a+b}{a}}={frac {a}{b}}=varphi .}$^[1]

Один из методов определения стоимости φ - начать с левой дроби. Упростив дробь и подставив в b / a = 1 /φ,

${displaystyle {frac {a+b}{a}}={frac {a}{a}}+{frac {b}{a}}=1+{frac {b}{a}}=1+{frac {1}{varphi }}.}$

Следовательно,

${displaystyle 1+{frac {1}{varphi }}=varphi .}$

Умножение на φ дает

${displaystyle varphi +1=varphi ^{2}}$

который может быть преобразован в

${displaystyle {varphi }^{2}-varphi -1=0.}$

С использованием квадратичная формула, получены два решения:

${displaystyle {frac {1+{sqrt {5}}}{2}}=1.618,033,988,7dots }$ и ${displaystyle {frac {1-{sqrt {5}}}{2}}=-0.618,033,988,7dots }$

Потому что φ это отношение положительных величин, φ обязательно положительный:

${displaystyle varphi ={frac {1+{sqrt {5}}}{2}}=1.61803,39887dots }$^[2]

История

Смотрите также: Математика и искусство и Число Фибоначчи § История

В соответствии с Марио Ливио,

Некоторые из величайших математических умов всех возрастов из Пифагор и Евклид в древняя Греция через средневекового итальянского математика Леонардо Пизанский и астроном эпохи Возрождения Иоганн Кеплер, современным ученым, таким как оксфордский физик Роджер Пенроуз, потратили бесконечные часы на это простое соотношение и его свойства. ... Биологи, художники, музыканты, историки, архитекторы, психологи и даже мистики размышляли и обсуждали причины его повсеместности и привлекательности. Фактически, будет справедливо сказать, что золотое сечение вдохновляло мыслителей всех дисциплин, как никакое другое число в истории математики.^[14]

— Золотое сечение: история Фи, самого удивительного числа в мире

Древнегреческий математики впервые изучали то, что мы теперь называем золотым сечением, поскольку оно часто встречается в геометрия;^[15] разделение линии на «крайнее и среднее отношение» (золотое сечение) важно в геометрии регулярного пентаграммы и пятиугольники.^[16] Согласно одной истории, математик V века до нашей эры Гиппас обнаружил, что золотое сечение не является ни целым числом, ни дробью ( иррациональный номер ), удивительно Пифагорейцы.^[17] Евклид с Элементы (c. 300 г. до н.э.) предоставляет несколько предложения и их доказательства, использующие золотое сечение,^[18][b] и содержит его первое известное определение, которое выглядит следующим образом:^[19]

Говорят, что прямая линия разрезана в крайнем и среднем соотношении, когда, как вся линия относится к большему сегменту, так и больше к меньшему.^[20][c]

Майкл Маэстлин, первым записавшим десятичную аппроксимацию отношения

В течение следующего тысячелетия золотое сечение изучалось периферийно. Абу Камил (ок. 850–930) использовал его в своих геометрических вычислениях пятиугольников и декагонов; его сочинения повлияли на Фибоначчи (Леонардо Пизанский) (ок. 1170–1250), который использовал соотношение в связанных задачах геометрии, хотя никогда не связывал его с серия чисел, названная его именем.^[22]

Лука Пачоли назвал свою книгу Divina пропорционально (1509 ) после соотношения, и исследовал его свойства, включая его появление в некоторых Платоновы тела.^[11][23] Леонардо да Винчи, который иллюстрировал вышеупомянутую книгу, назвал соотношение sectio aurea («золотое сечение»).^[24] Математики XVI века, такие как Рафаэль Бомбелли решал геометрические задачи с помощью соотношения.^[25]

Немецкий математик Саймон Якоб (ум. 1564) заметил, что последовательные числа Фибоначчи сходятся к золотому сечению;^[26] это было заново открыто Иоганн Кеплер в 1608 г.^[27] Первый известный десятичный приближение (обратного) золотого сечения было заявлено как "около 0,6180340" в 1597 г. Майкл Маэстлин из Тюбингенский университет в письме своему бывшему ученику Кеплеру.^[28] В том же году Кеплер написал Маэстлину из Треугольник Кеплера, который сочетает в себе золотое сечение с теорема Пифагора. Кеплер сказал об этом:

У геометрии есть два великих сокровища: одно - это теорема Пифагора, другое - деление прямой на крайнее и среднее отношение. Первое мы можем сравнить с массой золота, второе - с драгоценным камнем.^[7]

Математики 18 века Абрахам де Муавр, Даниэль Бернулли, и Леонард Эйлер использовал формулу, основанную на золотом сечении, которая находит значение числа Фибоначчи на основе его расположения в последовательности; в 1843 году это было заново открыто Жак Филипп Мари Бине, в честь которого она была названа «формулой Бине».^[29] Мартин Ом впервые использовал немецкий термин Goldener Schnitt («золотое сечение») для описания соотношения в 1835 году.^[30] Джеймс Салли использовал эквивалентный английский термин в 1875 году.^[31]

К 1910 году математик Марк Барр начал использовать Греческая буква Фи (φ) как символ для золотого сечения.^[32][d] Он также был представлен тау (τ), первая буква древнегреческий τομή («вырезать» или «разрезать»).^[35][36]

Между 1973 и 1974 гг. Роджер Пенроуз развитый Плитка Пенроуза, узор, относящийся к золотому сечению как по соотношению площадей двух ромбических плиток, так и по их относительной частоте в узоре.^[37] Это привело к Дэн Шехтман открытие в начале 80-х квазикристаллы,^[38][39] некоторые из которых выставлены икосаэдрическая симметрия.^[40][41]

Приложения и наблюдения

Архитектура

Дальнейшая информация: Математика и архитектура

Вид на минарет со двора Великая мечеть Кайруана

Геометрический анализ более ранних исследований 2004 г. Великая мечеть Кайруана (670) показывает применение золотого сечения в большей части дизайна.^[42] Они нашли соотношения, близкие к золотому сечению, в общей планировке и в размерах молитвенного пространства, двора и минарет. Однако области с соотношением, близким к золотому сечению, не входили в первоначальный план и, вероятно, были добавлены при реконструкции.^[42]

Было высказано предположение, что золотое сечение использовалось дизайнерами Площадь Накш-э-Джахан (1629), а соседние Мечеть Лотфолла.^[43]

Швейцарцы архитектор Ле Корбюзье, известный своим вкладом в современное международный стиль, сосредоточил свою философию дизайна на системах гармонии и пропорций. Вера Ле Корбюзье в математический порядок Вселенной была тесно связана с золотым сечением и рядами Фибоначчи, которые он описал как «ритмы, очевидные для глаза и ясные в их отношениях друг с другом. И эти ритмы лежат в основе человеческая деятельность. Они звучат в человеке органической неизбежностью, той же прекрасной неизбежностью, которая заставляет детей, стариков, дикарей и ученых вычеркивать Золотое сечение ».^[44][45]

Ле Корбюзье явно использовал золотое сечение в своем Модулор система для шкала из архитектурная пропорция. Он видел эту систему как продолжение давней традиции Витрувий Леонардо да Винчи "Витрувианский человек ", работа Леон Баттиста Альберти, и другие, которые использовали пропорции человеческого тела для улучшения внешнего вида и функций архитектура.

Помимо золотого сечения Ле Корбюзье основал систему на человеческие измерения, Числа Фибоначчи, и двойной блок. Он довел предположение о золотом сечении в человеческих пропорциях до крайности: он разделил высоту своей модели человеческого тела на уровне пупка на две части в золотом сечении, затем разделил эти части в золотом сечении на коленях и горле; он использовал эти пропорции золотого сечения в Модулор система. Вилла Штайн 1927 года Ле Корбюзье в Garches проиллюстрировано приложение системы Modulor. Прямоугольный план, фасад и внутренняя структура виллы очень похожи на золотые прямоугольники.^[46]

Другой швейцарский архитектор, Марио Ботта, основывает многие свои проекты на геометрических фигурах. Несколько частных домов, которые он спроектировал в Швейцарии, состоят из квадратов и кругов, кубов и цилиндров. В доме, который он спроектировал в Ориглио, золотое сечение - это соотношение между центральной и боковыми частями дома.^[47]

Изобразительное искусство

Дальнейшая информация: Математика и искусство и История эстетики до 20 века

Леонардо иллюстрация додекаэдра из Пачоли с Divina пропорционально (1509)

Divina пропорционально (Божественная пропорция), трехтомник Лука Пачоли, был опубликован в 1509 году. Пачоли, а Францисканский монах, был известен в основном как математик, но он также был обучен и очень интересовался искусством. Divina пропорционально исследовал математику золотого сечения. Хотя часто говорят, что Пачоли защищал применение золотого сечения для получения приятных гармоничных пропорций, Ливио указывает, что интерпретация была прослежена до ошибки в 1799 году, и что Пачоли фактически выступал за Витрувианский система рациональных пропорций.^[48] Пачоли также видел католическое религиозное значение в соотношении, что привело к названию его работы.

Леонардо да Винчи иллюстрации многогранники в Divina пропорционально^[49] заставили некоторых предположить, что он использовал золотое сечение в своих картинах. Но предположение, что его Мона Лиза, например, использует пропорции золотого сечения, что не подтверждается собственными трудами Леонардо.^[50] Точно так же, хотя Витрувианский человек часто отображается в связи с золотым сечением, пропорции фигуры на самом деле не соответствуют ему, а в тексте упоминаются только отношения целых чисел.^[51][52]

Сальвадор Дали под влиянием произведений Матила Гика,^[53] явно использовал золотое сечение в своем шедевре, Таинство Тайной вечери. Размеры полотна - золотой прямоугольник. Сверху и сзади подвешен огромный додекаэдр в перспективе, так что края кажутся друг другу в золотом сечении. Иисус и доминирует в композиции.^[50][54]

Статистическое исследование 565 произведений искусства разных великих художников, проведенное в 1999 году, показало, что эти художники не использовали золотое сечение в размере своих полотен. Исследование пришло к выводу, что среднее соотношение двух сторон изученных картин составляет 1,34, при этом средние значения для отдельных художников варьируются от 1,04 (Гойя) до 1,46 (Беллини).^[55] С другой стороны, Пабло Тосто перечислил более 350 работ известных художников, в том числе более 100 работ с холстами с золотым прямоугольником и пропорциями корня 5, а также другие с пропорциями, такими как корень 2, 3, 4 и 6.^[56]

Изображение пропорций в средневековой рукописи. В соответствии с Ян Чихольд: "Пропорции страницы 2: 3. Пропорции полей 1: 1: 2: 3. Пропорции области текста в золотом сечении."^[57]

Книги и дизайн

Основная статья: Каноны построения страницы

В соответствии с Ян Чихольд,

Было время, когда отклонения от действительно красивых пропорций страницы 2: 3, 1: √3 и золотого сечения были редкостью. Многие книги, выпущенные между 1550 и 1770 годами, демонстрируют эти пропорции с точностью до полмиллиметра.^[58]

Согласно некоторым источникам, золотое сечение используется в повседневном дизайне, например, в пропорциях игральных карт, открыток, плакатов, пластин переключателя света и широкоэкранных телевизоров.^{[59][60][61][62]}

Музыка

Эрно Лендваи анализы Бела Барток работает как основанная на двух противоположных системах: золотом сечении и акустическая шкала,^[63] хотя другие ученые-музыковеды отвергают этот анализ.^[64] Французский композитор Эрик Сати использовал золотое сечение в нескольких своих произведениях, в том числе Sonneries de la Rose + Croix. Золотое сечение также проявляется в организации разделов в музыке Дебюсси с Reflets dans l'eau (Размышления в воде), из Изображений (1-я серия, 1905 г.), в которой «последовательность клавиш обозначена интервалами 34, 21, 13 и 8, а основная кульминация находится в позиции фи».^[65]

Музыковед Рой Ховат заметил, что формальные границы Дебюсси La Mer точно соответствуют золотому сечению.^[66] Трезизе считает внутреннее свидетельство "замечательным", но предупреждает, что никакие письменные или заявленные свидетельства не предполагают, что Дебюсси сознательно стремился к таким масштабам.^[67]

Жемчужные барабаны позиционирует вентиляционные отверстия на своих моделях Masters Premium на основе золотого сечения. Компания утверждает, что это устройство улучшает басы, и подала заявку на патент по этому нововведению.^[68]

Хотя Хайнц Болен предложил неоктавно-повторяющийся 833 цента шкала на основе сочетание тонов, в настройке предусмотрены отношения, основанные на золотом сечении. В качестве музыкального интервала соотношение 1,618 ... составляет 833,090 ... центов (Играть в ).^[69]

Природа

Деталь блюдца растения, Эониум табулиформный, показывающий многоспиральное расположение (парастихия )

Основная статья: Узоры в природе

Смотрите также: Число Фибоначчи § Природа

Иоганн Кеплер писал, что «образ мужчины и женщины проистекает из божественной пропорции. На мой взгляд, размножение растений и потомство животных находятся в одном соотношении».^[70]

Психолог Адольф Цейзинг отметил, что золотое сечение появилось в филлотаксис и аргументировал это закономерности в природе что золотое сечение было универсальным законом.^[71][72] Цейзинг написал в 1854 г. ортогенетический закон «стремления к красоте и полноте в царстве природы и искусства».^[73]

В 2010 г. журнал Наука сообщили, что золотое сечение присутствует на атомном уровне в магнитном резонансе спинов в кристаллах ниобата кобальта.^[74]

Однако некоторые утверждали, что многие очевидные проявления золотого сечения в природе, особенно в отношении размеров животных, являются вымышленными.^[75]

Оптимизация

Золотое сечение - ключ к успеху. поиск золотого сечения.

Математика

Иррациональность

Золотое сечение - это иррациональный номер. Ниже приведены два коротких доказательства иррациональности:

Противоречие из низшего выражения

Если φ мы рациональный, то это будет отношение сторон прямоугольника к целым сторонам (прямоугольник, составляющий всю диаграмму). Но это также будет отношение целых сторон меньшего прямоугольника (самая правая часть диаграммы), полученного удалением квадрата. Последовательность убывающих длин сторон целого числа, образованная удалением квадратов, не может продолжаться бесконечно, потому что целые числа имеют нижнюю границу, поэтому φ не может быть рациональным.

Напомним, что:

целое - это более длинная часть плюс более короткая часть;

целое относится к более длинной части, а более длинная - к более короткой.

Если мы назовем все п и более длинная часть м, то второе утверждение выше становится

п должен м в качестве м должен п − м,

или, алгебраически

${displaystyle {frac {n}{m}}={frac {m}{n-m}}.qquad (*)}$

Сказать, что золотое сечение φ рационально означает, что φ это дробь п/м куда п и м целые числа. Мы можем взять п/м быть в самые низкие сроки и п и м быть позитивным. Но если п/м находится в низших терминах, то идентичность, помеченная (*) выше, говорит м/(п − м) находится в еще более низких сроках. Это противоречие следует из предположения, что φ рационально.

По иррациональности √5

Еще одно короткое доказательство - возможно, более широко известное - иррациональности золотого сечения использует закрытие рациональных чисел при сложении и умножении. Если ${displaystyle extstyle {frac {1+{sqrt {5}}}{2}}}$ рационально, то ${displaystyle extstyle 2left({frac {1+{sqrt {5}}}{2}}ight)-1={sqrt {5}}}$ также рационально, что является противоречием, если уже известно, что квадратный корень из не-квадрат натуральное число иррационально.

Минимальный многочлен

Золотое сечение также алгебраическое число и даже алгебраическое целое число. Она имеет минимальный многочлен

${displaystyle x^{2}-x-1.}$

Имея степень 2, этот многочлен фактически имеет два корня, второй из которых является сопряженным золотым сечением.

Конъюгат золотого сечения

Сопряженный корень минимальному многочлену x² - x - 1 - это

${displaystyle -{frac {1}{varphi }}=1-varphi ={frac {1-{sqrt {5}}}{2}}=-0.61803,39887dots .}$

Абсолютное значение этой величины (≈ 0,618) соответствует отношению длин, взятому в обратном порядке (меньшая длина сегмента по сравнению с большей длиной сегмента, б / а), и иногда его называют конъюгат золотого сечения^[13] или же соотношение серебра.^[e][76] Обозначается здесь заглавной Фи (${displaystyle Phi }$):

${displaystyle Phi ={1 over varphi }=varphi ^{-1}=0.61803,39887ldots .}$

В качестве альтернативы, ${displaystyle Phi }$ можно выразить как

${displaystyle Phi =varphi -1=1.61803,39887ldots -1=0.61803,39887ldots .}$

Это иллюстрирует уникальное свойство золотого сечения среди положительных чисел, которое

${displaystyle {1 over varphi }=varphi -1,}$

или его обратное:

${displaystyle {1 over Phi }=Phi +1.}$

Это означает 0,61803 ...: 1 = 1: 1,61803 ....

Альтернативные формы

Аппроксимация обратного золотого сечения конечными цепными дробями или отношениями чисел Фибоначчи

Формула φ = 1 + 1/φ может быть расширен рекурсивно, чтобы получить непрерывная дробь для золотого сечения:^[77]

${displaystyle varphi =[1;1,1,1,dots ]=1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}}$

и его обратное:

${displaystyle varphi ^{-1}=[0;1,1,1,dots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}}$

В сходящиеся этих непрерывных дробей (1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ... или 1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ...) - отношения последовательных Числа Фибоначчи.

Уравнение φ² = 1 + φ аналогично производит непрерывный квадратный корень:

${displaystyle varphi ={sqrt {1+{sqrt {1+{sqrt {1+{sqrt {1+cdots }}}}}}}}.}$

Можно вывести бесконечный ряд, чтобы выразить φ:^[78]

${displaystyle varphi ={frac {13}{8}}+sum _{n=0}^{infty }{frac {(-1)^{n+1}(2n+1)!}{4^{2n+3}n!(n+2)!}}.}$

Также:

${displaystyle varphi =1+2sin(pi /10)=1+2sin 18^{circ }}$

${displaystyle varphi ={1 over 2}csc(pi /10)={1 over 2}csc 18^{circ }}$

${displaystyle varphi =2cos(pi /5)=2cos 36^{circ }}$

${displaystyle varphi =2sin(3pi /10)=2sin 54^{circ }.}$

Это соответствует тому факту, что длина диагонали правильного пятиугольника равна φ раз больше длины его стороны, и аналогичные отношения в пентаграмма.

Геометрия

Примерно и верно золотые спирали. В зеленый спираль состоит из четверти окружностей, касающихся внутренней части каждого квадрата, а красный спираль - это Золотая спираль, особый вид логарифмическая спираль. Появляются перекрывающиеся части желтый. Длина стороны одного квадрата, деленная на сторону следующего меньшего квадрата, и есть золотое сечение.

Номер φ часто появляется в геометрия, особенно в фигурах с пятиугольником симметрия.Длина обычного пятиугольник с диагональ является φ умноженное на его сторону. Вершины правильного икосаэдр те из три взаимно ортогональный золотые прямоугольники.

Нет известного генерала алгоритм равномерно расположить заданное количество узлов на сфере для любого из нескольких определений равномерного распределения (см., например, Проблема Томсона ). Однако полезное приближение получается из разделения сферы на параллельные полосы равных площадь поверхности и размещение по одному узлу в каждой полосе на долготах, разделенных золотым сечением круга, т.е. 360 ° /φ ≅ 222,5 °. Этим методом были расставлены 1500 зеркал студенческого собрания. спутник Звездный свет-3.^[79]

Разделение отрезка на внутреннее деление

Разделение отрезка на внутреннее деление по золотому сечению

1. Имея отрезок AB, постройте перпендикуляр BC в точке B так, чтобы BC составлял половину длины AB. Нарисуйте гипотенуза AC.
2. Нарисуйте дугу с центром C и радиусом BC. Эта дуга пересекает гипотенузу AC в точке D.
3. Нарисуйте дугу с центром A и радиусом AD. Эта дуга пересекает исходный отрезок AB в точке S. Точка S делит исходный отрезок AB на отрезки AS и SB с длинами в золотом сечении.

Разделение линейного сегмента внешним делением

Разделение отрезка линии внешним делением по золотому сечению

1. Проведите отрезок AS и постройте от точки S отрезок SC, перпендикулярный AS и такой же длины, как AS.
2. Разделите пополам отрезок AS с M.
3. Дуга окружности вокруг M с радиусом MC пересекает в точке B прямую, проходящую через точки A и S (также известную как продолжение AS). Отношение AS к построенному сегменту SB - это золотое сечение.

Примеры применения вы можете увидеть в статьях Пентагон с заданной длиной стороны, Десятиугольник с заданной описанной окружностью и Десятиугольник с заданной длиной стороны.

Оба вышеперечисленных отображаются по-разному алгоритмы производить геометрические конструкции которые определяют два согласованных отрезки линии где отношение более длинного к более короткому - это золотое сечение.

Золотой треугольник, пятиугольник и пентаграмма

Золотой треугольник. Угол с двойной красной аркой составляет 36 градусов, или ${displaystyle {frac {pi }{5}}}$ радианы.

Золотой треугольник

В золотой треугольник можно охарактеризовать как равнобедренный треугольник ABC со свойством, что деление пополам угол C дает новый треугольник CXB, который является подобный треугольник к оригиналу.

Если угол BCX = α, то XCA = α из-за деления пополам и CAB = α из-за аналогичных треугольников; ABC = 2α из исходной равнобедренной симметрии и BXC = 2α по подобию. Сумма углов в треугольнике составляет 180 °, поэтому 5α = 180, что дает α = 36 °. Таким образом, углы золотого треугольника составляют 36 ° -72 ° -72 °. Углы оставшегося тупого равнобедренного треугольника AXC (иногда называемого золотым гномоном) составляют 36 ° -36 ° -108 °.

Предположим, что XB имеет длину 1, и мы называем BC длиной φ. Из-за равнобедренных треугольников XC = XA и BC = XC, это также длина φ. Длина AC = AB, следовательно, равна φ + 1. Но треугольник ABC подобен треугольнику CXB, поэтому AC / BC = BC / BX, AC /φ = φ / 1, поэтому AC также равно φ². Таким образом φ² = φ + 1, подтверждая, что φ действительно золотое сечение.

Точно так же отношение площади большего треугольника AXC к меньшему CXB равно φ, в то время как обратный коэффициент φ - 1.

Пентагон

В правильный пятиугольник отношение диагонали к стороне - это золотое сечение, а пересекающиеся диагонали разделяют друг друга в золотом сечении.^[11]

Строительство Одома

Пусть A и B - середины сторон EF и ED равностороннего треугольника DEF. Продлите AB, чтобы встретить описанную окружность DEF в C.
${displaystyle { frac {|AB|}{|BC|}}={ frac {|AC|}{|AB|}}=phi }$

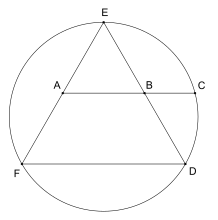
Джордж Одом дал удивительно простую конструкцию для φ с участием равностороннего треугольника: если равносторонний треугольник вписан в круг и отрезок линии, соединяющий середины двух сторон, образуется так, чтобы пересекать круг в любой из двух точек, то эти три точки находятся в золотой пропорции. Этот результат является прямым следствием теорема о пересечении хорд и может быть использован для построения правильного пятиугольника, конструкция, которая привлекла внимание известного канадского геометра. Х. С. М. Коксетер кто опубликовал это от имени Одома в виде диаграммы в Американский математический ежемесячный журнал сопровождается единственным словом «вот!» ^[80]

Пентаграмма

Пентаграмма, окрашенная для выделения отрезков разной длины. Четыре длины находятся в золотом соотношении друг к другу.

Золотое сечение играет важную роль в геометрии пентаграммы. Каждое пересечение ребер разделяет другие ребра в золотой пропорции. Кроме того, отношение длины более короткого сегмента к отрезку, ограниченному двумя пересекающимися краями (сторона пятиугольника в центре пентаграммы), равно φ, как показано на четырехцветной иллюстрации.

Пентаграмма включает десять равнобедренные треугольники: пять острый и пять тупой равнобедренные треугольники. Во всех них отношение длинной стороны к короткой стороне равно φ. Острые треугольники - это золотые треугольники. Тупые равнобедренные треугольники - золотые гномоны.

Теорема Птолемея

Золотое сечение в правильном пятиугольнике можно вычислить с помощью Теорема Птолемея.

Свойства золотого сечения правильного пятиугольника можно подтвердить, применив Теорема Птолемея в четырехугольник, образованный удалением одной из его вершин. Если длинный край и диагонали четырехугольника равны б, а короткие края - а, то теорема Птолемея дает б² = а² + ab что дает

${displaystyle {b over a}={{1+{sqrt {5}}} over 2}.}$

Масштабность треугольников

Рассмотрим треугольник со сторонами длины а, б, и c в порядке убывания. Определите "масштабность" треугольника как меньшее из двух соотношений. а/б и б/c. Масштабность всегда меньше φ и может быть максимально приближен к φ.^[81]

Треугольник, стороны которого образуют геометрическую прогрессию

Если стороны треугольника образуют геометрическая прогрессия и находятся в соотношении 1: р : р², куда р это обычное отношение, тогда р должен находиться в диапазоне φ−1 < р < φ, что является следствием неравенство треугольника (сумма любых двух сторон треугольника должна быть строго больше длины третьей стороны). Если р = φ тогда две более короткие стороны равны 1 и φ но их сумма φ², таким образом р < φ. Аналогичный расчет показывает, что р > φ−1. Треугольник, стороны которого находятся в соотношении 1: √φ : φ прямоугольный треугольник (потому что 1 + φ = φ²) известный как Треугольник Кеплера.^[82]

Золотой треугольник, ромб и ромбический триаконтаэдр

Один из ромбов ромбического триаконтаэдра

Все грани ромбического триаконтаэдра - золотые ромбы.

А золотой ромб это ромб диагонали которого находятся в золотом сечении. В ромбический триаконтаэдр это выпуклый многогранник у него очень особенное свойство: все его грани - золотые ромбы. в ромбический триаконтаэдр то двугранный угол Между любыми двумя соседними ромбами 144 °, что в два раза больше равнобедренного угла золотого треугольника и в четыре раза больше его самого острого угла.^[83]

Связь с последовательностью Фибоначчи

Математика золотого сечения и Последовательность Фибоначчи тесно взаимосвязаны. Последовательность Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...

А выражение в закрытой форме для последовательности Фибоначчи используется золотое сечение:

${displaystyle Fleft(night)={{varphi ^{n}-(1-varphi )^{n}} over {sqrt {5}}}={{varphi ^{n}-(-varphi )^{-n}} over {sqrt {5}}}.}$

А Спираль Фибоначчи который аппроксимирует золотую спираль, используя размеры квадратов последовательности Фибоначчи до 34. Спираль рисуется, начиная с внутреннего квадрата 1 × 1, и продолжается наружу к последовательно большим квадратам.

Золотые квадраты с Т-разветвление

Золотой квадратный фрактал

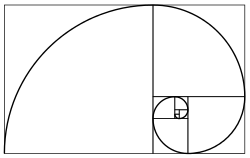
Золотое сечение - это предел соотношений последовательных членов последовательности Фибоначчи (или любой последовательности, подобной Фибоначчи), как показано Кеплер:^[84]

${displaystyle lim _{n o infty }{frac {F_{n+1}}{F_{n}}}=varphi .}$

Другими словами, если число Фибоначчи делится на его непосредственного предшественника в последовательности, частное приблизительно равно φ; например, 987/610≈ 1.6180327868852. Эти приближения попеременно ниже и выше, чем φ, и сходятся к φ когда числа Фибоначчи увеличиваются, и:

${displaystyle sum _{n=1}^{infty }|F_{n}varphi -F_{n+1}|=varphi .}$

В более общем смысле:

${displaystyle lim _{n o infty }{frac {F_{n+a}}{F_{n}}}=varphi ^{a},}$

где выше отношения последовательных членов последовательности Фибоначчи, является случаем, когда ${displaystyle a=1.}$

Кроме того, последовательные степени φ подчиняться Фибоначчи повторение:

${displaystyle varphi ^{n+1}=varphi ^{n}+varphi ^{n-1}.}$

Это тождество допускает любой многочлен от φ сводится к линейному выражению. Например:

${displaystyle {egin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi )-5varphi ^{2}+4&=3[(varphi +1)+varphi ]-5(varphi +1)+4&=varphi +2approx 3.618.end{aligned}}}$

Приведение к линейному выражению может быть выполнено за один шаг с помощью отношения

${displaystyle varphi ^{k}=F_{k}varphi +F_{k-1},}$

куда ${displaystyle F_{k}}$ это k-е число Фибоначчи.

Однако это не особенное свойство φ, потому что многочлены в любом решении Икс к квадратное уровненеие можно уменьшить аналогичным образом, применив:

${displaystyle x^{2}=ax+b}$

для заданных коэффициентов а, б такой, что Икс удовлетворяет уравнению. В более общем смысле, любой рациональная функция (с рациональными коэффициентами) корня неприводимой пМногочлен -й степени над рациональными числами сводится к полиному степени п ‒ 1. Сформулировано в терминах теория поля, если α - корень неприводимой пмногочлен -й степени, то ${displaystyle mathbb {Q} (alpha )}$ имеет степень п над ${displaystyle mathbb {Q} }$, с основанием ${displaystyle {1,alpha ,dots ,alpha ^{n-1}}.}$

Симметрии

Золотое сечение и обратное золотое сечение ${displaystyle varphi _{pm }=(1pm {sqrt {5}})/2}$ обладают набором симметрий, которые их сохраняют и связывают. Оба они сохранены дробно-линейные преобразования ${displaystyle x,1/(1-x),(x-1)/x,}$ - этот факт соответствует тождеству и определению квадратного уравнения. Далее они меняются местами тремя отображениями ${displaystyle 1/x,1-x,x/(x-1)}$ - они взаимны, симметричны относительно ${displaystyle 1/2}$, и (проективно) симметрично относительно 2.

Более глубоко эти карты образуют подгруппу модульная группа ${displaystyle operatorname {PSL} (2,mathbf {Z} )}$ изоморфен симметричная группа на 3 буквы, ${displaystyle S_{3},}$ соответствующий стабилизатор из набора ${displaystyle {0,1,infty }}$ 3-х стандартных точек на проективная линия, а симметрии соответствуют фактор-отображению ${displaystyle S_{3} o S_{2}}$ - подгруппа ${displaystyle C_{3}<S_{3}}$ состоящий из 3-циклов и тождественного ${displaystyle ()(01infty )(0infty 1)}$ фиксирует два числа, в то время как 2 цикла меняют их местами, таким образом реализуя карту.

Другие свойства

Золотое сечение имеет простейшее выражение (и самую медленную сходимость) в виде разложения в непрерывную дробь любого иррационального числа (см. Альтернативные формы над). По этой причине это один из худшие случаи из Аппроксимационная теорема Лагранжа и это экстремальный случай Неравенство Гурвица за Диофантовы приближения. Возможно, поэтому углы, близкие к золотому сечению, часто появляются в филлотаксис (рост растений).^[85]

Определяющий квадратичный полином и сопряженное отношение приводят к десятичным значениям, дробная часть которых совпадает с φ:

${displaystyle varphi ^{2}=varphi +1=2.618dots }$

${displaystyle {1 over varphi }=varphi -1=0.618dots .}$

Последовательность полномочий φ содержит эти значения 0,618 ..., 1,0, 1,618 ..., 2,618 ...; вообще, любая сила φ равно сумме двух непосредственно предшествующих степеней:

${displaystyle varphi ^{n}=varphi ^{n-1}+varphi ^{n-2}=varphi cdot operatorname {F} _{n}+operatorname {F} _{n-1}.}$

В результате легко разложить любую степень φ в несколько φ и постоянная. Кратное и константа всегда являются смежными числами Фибоначчи. Это приводит к другому свойству положительных степеней φ:

Если ${displaystyle lfloor n/2-1floor =m}$, тогда:

${displaystyle ! varphi ^{n}=varphi ^{n-1}+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2-2m}}$

${displaystyle ! varphi ^{n}-varphi ^{n-1}=varphi ^{n-2}.}$

Когда золотое сечение используется в качестве основы система счисления (видеть База золотого сечения, иногда дублированный финарный или же φ-нари) каждое целое число имеет завершающее представление, несмотря на φ быть иррациональным, но каждая дробь имеет представление без конца.

Золотое сечение - это основная единица из поле алгебраических чисел ${displaystyle mathbb {Q} ({sqrt {5}})}$ и является Число Писот – Виджаярагаван.^[86] В поле ${displaystyle mathbb {Q} ({sqrt {5}})}$ у нас есть ${displaystyle varphi ^{n}={{L_{n}+F_{n}{sqrt {5}}} over 2}}$, куда ${displaystyle L_{n}}$ это ${displaystyle n}$-го Число Лукаса.

Золотое сечение также появляется в гиперболическая геометрия, как максимальное расстояние от точки на одной стороне идеальный треугольник к ближайшей из двух других сторон: это расстояние, длина стороны равносторонний треугольник образованный точками касания окружности, вписанной в идеальный треугольник, является ${displaystyle 4log(varphi )}$.^[87]

Золотое сечение появляется в теории модульные функции также. Позволять

${displaystyle R(q)={cfrac {q^{1/5}}{1+{cfrac {q}{1+{cfrac {q^{2}}{1+{cfrac {q^{3}}{1+ddots }}}}}}}}.}$

потом

${displaystyle R(e^{-2pi })={sqrt {varphi {sqrt {5}}}}-varphi ,quad R(e^{-2pi {sqrt {5}}})={frac {sqrt {5}}{1+left(5^{frac {3}{4}}(varphi -1)^{frac {5}{2}}-1ight)^{frac {1}{5}}}}-varphi .}$

Также если ${displaystyle a,bin mathbb {R} ^{+}}$ и ${displaystyle ab=pi ^{2}}$, тогда^[88]

${displaystyle (R(e^{-2a})+varphi )(R(e^{-2b})+varphi )=varphi {sqrt {5}}.}$

Десятичное разложение

Десятичное разложение золотого сечения можно вычислить непосредственно из выражения

${displaystyle varphi ={1+{sqrt {5}} over 2}}$

с √5 ≈ 2.2360679774997896964 OEIS: A002163. В квадратный корень из 5 можно рассчитать с помощью Вавилонский метод, начиная с начальной оценки, такой как Иксφ = 2 и повторение

${displaystyle x_{n+1}={frac {(x_{n}+5/x_{n})}{2}}}$

за п = 1, 2, 3, ..., пока разница между Икс_п и Икс_п−1 становится нулем до желаемого количества цифр.

Вавилонский алгоритм для √5 эквивалентно Метод Ньютона для решения уравнения Икс² - 5 = 0. В более общем виде метод Ньютона может применяться непосредственно к любым алгебраическое уравнение, включая уравнение Икс² - x - 1 = 0, что определяет золотое сечение. Это дает итерацию, которая сходится к самому золотому сечению,

${displaystyle x_{n+1}={frac {x_{n}^{2}+1}{2x_{n}-1}},}$

для соответствующей начальной оценки Иксφ Такие как Иксφ = 1. Более быстрый способ - переписать уравнение в виде Икс − 1 − 1/Икс = 0, и в этом случае итерация Ньютона становится

${displaystyle x_{n+1}={frac {x_{n}^{2}+2x_{n}}{x_{n}^{2}+1}}.}$

Все эти итерации сходятся квадратично; то есть каждый шаг примерно удваивает количество правильных цифр. Таким образом, золотое сечение относительно легко вычислить с помощью произвольная точность. Время, необходимое для вычисления п цифры золотого сечения пропорциональны времени, необходимому для деления двух п-значные числа. Это значительно быстрее, чем известные алгоритмы для трансцендентные числа π и е.

Легко программируемая альтернатива с использованием только целочисленной арифметики - вычислить два больших последовательных числа Фибоначчи и разделить их. Отношение чисел Фибоначчи F ₂₅₀₀₁ и F ₂₅₀₀₀, каждая из которых превышает 5000 цифр, дает более 10 000 значащих цифр золотого сечения.

Десятичное разложение золотого сечения φ^[3] был рассчитан с точностью до двух триллионов (2×10¹² = 2 000 000 000 000) цифр.^[89]

Пирамиды

Дальнейшая информация: Математика и искусство

Правильная квадратная пирамида определяется ее средним прямоугольным треугольником, ребрами которого являются апофема пирамиды (a), полуоснование (b) и высота (h); также отмечается угол наклона лица. Математические пропорции b: h: a of ${displaystyle 1:{sqrt {varphi }}:varphi }$ и ${displaystyle 3:4:5}$ и ${displaystyle 1:4/pi :1.61899}$ представляют особый интерес по отношению к египетским пирамидам.

И египетские пирамиды, и обычные квадратные пирамиды похожие на них, можно проанализировать с точки зрения золотого сечения и других соотношений.

Математические пирамиды

Пирамида, в которой апофема (наклонная высота по биссектрисе грани) равна φ раз полубазу (половину ширины основания) иногда называют золотая пирамида. Равнобедренный треугольник, который является гранью такой пирамиды, может быть построен из двух половин разделенного по диагонали золотого прямоугольника (размером с полуоснование по апофемой), соединяющих края средней длины, чтобы образовать апофему. Высота этой пирамиды ${displaystyle {sqrt {varphi }}}$ умножить на полуоснование (то есть наклон грани равен ${displaystyle {sqrt {varphi }}}$); квадрат высоты равен площади лица, φ умножить на квадрат полуоснования.

Медиальный прямоугольный треугольник этой "золотой" пирамиды (см. схему), со сторонами ${displaystyle 1:{sqrt {varphi }}:varphi }$ интересен сам по себе, демонстрируя через теорема Пифагора отношения ${displaystyle {sqrt {varphi }}={sqrt {varphi ^{2}-1}}}$ или же ${displaystyle varphi ={sqrt {1+varphi }}}$. Этот Треугольник Кеплера^[90]- единственная пропорция прямоугольного треугольника с длиной ребер в геометрическая прогрессия,^[91][82] точно так же, как треугольник 3–4–5 является единственной пропорцией прямоугольного треугольника с длинами сторон в арифметическая прогрессия. Угол с касательная ${displaystyle {sqrt {varphi }}}$ соответствует углу, который сторона пирамиды образует по отношению к земле, 51,827 ... градусов (51 ° 49 '38 ").^[92]

Почти аналогичная форма пирамиды, но с рациональными пропорциями, описана в Математический папирус Райнда (источник значительной части современных знаний древнего Египетская математика ), основанный на треугольнике 3: 4: 5;^[93] наклон лица, соответствующий углу с касательной 4/3, составляет с двумя десятичными знаками 53,13 градуса (53 градуса и 8 минут). Наклонная высота или апофема составляет 5/3 или 1,666 ... раз от полуоснования. У папируса Райнда есть еще одна проблема пирамиды, опять же с рациональным наклоном (выраженным как наезд через подъем). Египетская математика не включала понятие иррациональных чисел,^[94] и рациональный обратный наклон (бег / подъем, умноженный на коэффициент 7, чтобы преобразовать в их условные единицы пальмы на локоть) использовался при строительстве пирамид.^[93]

Еще одна математическая пирамида с пропорциями, почти идентичными «золотой», - это пирамида с периметром, равным 2.π умноженное на высоту, или h: b = 4:π. Этот треугольник имеет угол наклона 51,854 ° (51 ° 51 '), что очень близко к 51,827 ° треугольника Кеплера. Эта пирамида отношения соответствует случайные отношения ${displaystyle {sqrt {varphi }}approx 4/pi }$.

Известны египетские пирамиды, очень близкие по пропорциям к этим математическим пирамидам.^[95][82]

Египетские пирамиды

В Великая пирамида в Гизе

Одна египетская пирамида, близкая к «золотой пирамиде», - это Великая пирамида в Гизе (также известная как пирамида Хеопса или Хуфу). Ее наклон 51 ° 52 'близок к наклону "золотой" пирамиды 51 ° 50' - и даже ближе к πнаклонная пирамида 51 ° 51 '. Однако несколько других математических теорий формы великой пирамиды, основанные на рациональных наклонах, оказались как более точными, так и более правдоподобными объяснениями наклона 51 ° 52 '.^[82]

В середине девятнадцатого века Фридрих Ребер изучал различные египетские пирамиды, в том числе пирамиды Хефрена, Menkaure, и некоторые из Гиза, Саккара, и Абусир группы. Он не применял золотое сечение к Великой пирамиде в Гизе, но вместо этого согласился с Джон Шэй Перринг что его соотношение сторон к высоте составляет 8: 5. Для всех других пирамид он применил измерения, относящиеся к треугольнику Кеплера, и заявил, что их длина целиком или половина стороны связана с их высотой по золотому сечению.^[96]

В 1859 г. пирамидолог Джон Тейлор неверно истолкованный Геродот (c. 440 г. до н.э.) как указание на то, что квадрат высоты Великой пирамиды равен площади одного из треугольников ее граней.^[f] Это привело Тейлора к утверждению, что в Великой пирамиде золотое сечение представлено отношением длины грани (высота склона, наклоненного под углом θ к земле) на половину длины стороны квадратного основания (эквивалентно секущий угла θ).^[98] Две указанные выше длины составляют примерно 186,4 метра (612 футов) и 115,2 метра (378 футов) соответственно.^[97] Отношение этих длин - золотое сечение, с точностью до большего числа цифр, чем любое из исходных измерений. По аналогии, Говард Вайс сообщил о высоте великой пирамиды 148,2 метра (486 футов) и половине основания 116,4 метра (382 фута), что дает 1,6189 для отношения наклонной высоты к половине основания, что опять же более точно, чем изменчивость данных.^[91]

Эрик Темпл Белл, математик и историк, утверждал в 1950 году, что египетская математика не поддержала бы способность вычислять наклонную высоту пирамид или отношение к высоте, за исключением пирамиды 3: 4: 5, поскольку 3: Треугольник 4: 5 был единственным прямоугольным треугольником, известным египтянам, и они не знали ни теорему Пифагора, ни какого-либо способа рассуждать об иррациональных числах, таких как π или же φ.^[99] Примерные геометрические задачи пирамидального дизайна в папирусе Райнда соответствуют различным рациональным наклонам.^[82]

Майкл Райс^[100] утверждает, что главные авторитеты в истории Египетская архитектура утверждали, что египтяне были хорошо знакомы с золотым сечением и что оно является частью математики пирамид, цитируя Гедона (1957).^[101] Историки науки давно обсуждают, обладали ли египтяне такими знаниями, утверждая, что его появление в Великой пирамиде - результат случайности.^[102]

Спорные наблюдения

Примеры спорных наблюдений за золотым сечением включают следующее:

Наутилус ракушки часто ошибочно называют золотыми пропорциями.

• Некоторые специфические пропорции тел многих животных (включая человека)^[103][104] и части раковин моллюсков^[5] часто утверждают, что они находятся в золотом сечении. Однако существует большой разброс в реальных показателях этих элементов у конкретных людей, и рассматриваемая пропорция часто значительно отличается от золотого сечения.^[103] Отношение последовательных фаланговых костей пальцев и пястной кости приблизительно соответствует золотому сечению.^[104] В наутилус оболочка, строительство которой происходит в логарифмическая спираль, часто цитируется, обычно с идеей, что любая логарифмическая спираль связана с золотым сечением, но иногда с утверждением, что каждая новая камера имеет золотую пропорцию по отношению к предыдущей.^[105] Однако измерения раковин наутилуса не подтверждают это утверждение.^[106]
• Историк Джон Ман заявляет, что страницы и текстовая область Библия Гутенберга были «основаны на форме золотого сечения». Однако, по его собственным меркам, отношение высоты к ширине страниц составляет 1,45.^[107]
• Исследования психологов, начиная с Густав Фехнер c. 1876 ​​г.,^[108] были разработаны, чтобы проверить идею о том, что золотое сечение играет роль в восприятии человеком Красота. Хотя Фехнер предпочел прямоугольные отношения, основанные на золотом сечении, более поздние попытки тщательно проверить такую ​​гипотезу были, в лучшем случае, безрезультатными.^[109][50]
• В области инвестирования некоторые практики технический анализ используйте золотое сечение для обозначения поддержки уровня цен или сопротивления росту цен на акции или товары; после значительных изменений цены вверх или вниз новые уровни поддержки и сопротивления предположительно обнаруживаются на уровне или около цен, связанных с начальной ценой через золотое сечение.^[110] Использование золотого сечения в инвестировании также связано с более сложными схемами, описываемыми Числа Фибоначчи (например. Волновой принцип Эллиотта и Восстановление Фибоначчи ). Однако другие рыночные аналитики опубликовали анализы, предполагающие, что эти проценты и закономерности не подтверждаются данными.^[111]

Парфенон

Многие пропорции Парфенон якобы демонстрируют золотое сечение, но оно в значительной степени дискредитировано.^[112]

В Парфенон фасад (ок. 432 г. до н.э.), а также элементы его фасада и других мест, как говорят некоторые, были очерчены золотыми прямоугольниками.^[113] Другие ученые отрицают, что у греков была эстетическая связь с золотым сечением. Например, Кейт Девлин говорит: «Конечно, часто повторяемое утверждение, что Парфенон в Афинах основан на золотом сечении, не подтверждается фактическими измерениями. На самом деле, вся история о греках и золотом сечении кажется безосновательной».^[114] Мидхат Дж. Газале утверждает, что «только Евклид ... математические свойства золотого сечения были изучены».^[115]

Из измерений 15 храмов, 18 монументальных гробниц, 8 саркофагов и 58 надгробных стел с пятого века до нашей эры до второго века нашей эры один исследователь пришел к выводу, что золотое сечение полностью отсутствует в греческой архитектуре классического пятого века до нашей эры, и почти отсутствует в течение следующих шести столетий.^[116]Более поздние источники, такие как Витрувий (первый век до нашей эры), обсуждают исключительно пропорции, которые могут быть выражены целыми числами, то есть соразмерные, а не иррациональные пропорции.

Современное искусство

Альберт Глейзес, Les Baigneuses (1912)

В Section d'Or («Золотое сечение») был коллективом художники, скульпторы, поэты и критики, связанные с Кубизм и Орфизм.^[117] Действуя с 1911 по 1914 год, они приняли это название, чтобы подчеркнуть, что кубизм представляет собой продолжение великой традиции, а не изолированное движение, и дань уважения математической гармонии, связанной с Жорж Сёра.^[118] Кубисты наблюдали в его гармонии, геометрической структуре движения и формы, примат идеи над природой, абсолютную научную ясность концепции.^[119] Однако, несмотря на общий интерес к математической гармонии, были ли картины, представленные в знаменитом 1912 году, Салон-де-ла-Раздел д'Ор Выставочное используемое золотое сечение в любых композициях определить сложнее. Ливио, например, утверждает, что они не^[120] и Марсель Дюшан сказал об этом в интервью.^[121] С другой стороны, анализ показывает, что Хуан Грис использовали золотое сечение при составлении работ, которые, вероятно, но не окончательно, были показаны на выставке.^{[121][122][123]} Историк искусства Дэниел Роббинс утверждал, что, помимо ссылки на математический термин, название выставки также относится к более раннему Bandeaux d'Or группа, с которой Альберт Глейзес и другие бывшие члены Abbaye de Créteil был вовлечен.^[124]

Пит Мондриан было сказано, что он широко использовал золотое сечение в своих геометрических картинах,^[125] хотя другие эксперты (в том числе критик Ив-Ален Буа ) дискредитировали эти утверждения.^[50][126]

Смотрите также

• Золотой угол
• Список работ с золотым сечением
• Металлическое средство
• Пластиковый номер
• Сакральная геометрия
• Сверхзолотое соотношение

Рекомендации

Пояснительные сноски

1. Если ограничение на a и b, каждое из которых больше нуля, снимается, тогда у этого уравнения фактически есть два решения, одно положительное и одно отрицательное. ϕ определяется как положительное решение. Отрицательное решение можно записать как ${displaystyle {frac {1-{sqrt {5}}}{2}}}$. Сумма двух решений равна одному, а произведение двух решений отрицательно.
2. Евклид, Элементы, Книга II, Предложение 11; Книга IV, предложения 10–11; Книга VI, Предложение 30; Книга XIII, Предложения 1–6, 8–11, 16–18.
3. "Κρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ λη πρὸς τὸ μεῖζον τμῆμα, οὕλτως τὸ μεῖζον πὸςτ.^[21]
4. По образцу классического греческого скульптора Фидий (ок. 490–430 до н. э.);^[33] Позже Барр писал, что считал маловероятным, что Фидий действительно использовал золотое сечение.^[34]
5. Не путать с серебряная середина, также известный как соотношение серебра.
6. Тейлор перевел Геродота: «Пирамида четырехгранная, каждая грань на каждой стороне 8 плетра, и высота равна ". Он истолковал это образно, и в 1860 г. Джон Гершель был первым из многих авторов, повторившим его ложное утверждение. В 2000 году Роджер Герц-Фишлер проследил за ошибкой до Тейлора.^[97]

Цитаты

1. «Сборник математических символов». Математическое хранилище. 2020-03-01. Получено 2020-08-10.
2. Вайсштейн, Эрик В. "Золотое сечение". mathworld.wolfram.com. Получено 2020-08-10.
3. OEIS: A001622
4. Ливио 2003 С. 3, 81.
5. Данлэп, Ричард А., Золотое сечение и числа Фибоначчи, World Scientific Publishing, 1997 г.
6. Евклид, Элементы, Книга 6, Определение 3.
7. Финк, Карл; Беман, Вустер Вудрафф; Смит, Дэвид Юджин (1903). Краткая история математики: авторизованный перевод книги доктора Карла Финка Geschichte der Elementar-Mathematik (2-е изд.). Чикаго: Open Court Publishing Co., стр. 223.
8. Саммерсон Джон, Небесные особняки: и другие очерки архитектуры (Нью-Йорк: W.W. Norton, 1963) с. 37. "И то же самое в архитектуре, прямоугольники представляющие эти и другие соотношения (например, «золотая огранка»). Единственная ценность этих соотношений в том, что они интеллектуально плодотворны и предполагают ритмы модульного дизайна ».
9. Джей Хэмбидж, Динамическая симметрия: греческая ваза, Нью-Хейвен, Коннектикут: Издательство Йельского университета, 1920.
10. Уильям Лидвелл, Критина Холден, Джилл Батлер, Универсальные принципы дизайна: междисциплинарный справочник, Глостер, Массачусетс: Rockport Publishers, 2003 г.
11. Пачоли, Лука. De Divina пропорционально, Лука Паганинем де Паганинус де Брешиа (Антонио Капелла) 1509, Венеция.
12. Строгац, Стивен (24 сентября 2012 г.). «Я, я и математика: контроль пропорций». Нью-Йорк Таймс.
13. Вайсштейн, Эрик В. «Сопряжение золотого сечения». MathWorld.
14. Ливио 2003, п. 6.
15. Ливио 2003, п. 4: «... линейное деление, которое Евклид определены для ... чисто геометрических целей ... "
16. Ливио 2003, стр. 7–8.
17. Ливио 2003, стр. 4–5.
18. Ливио 2003, п. 78.
19. Хеменуэй, Прия (2005). Божественная пропорция: Фи в искусстве, природе и науке. Нью-Йорк: Стерлинг. С. 20–21. ISBN  978-1-4027-3522-6.
20. Ливио 2003, п. 3.
21. Ричард Фицпатрик (переводчик) (2007). Элементы геометрии Евклида. п. 156. ISBN  978-0615179841.
22. Ливио 2003 С. 88–96.
23. Ливио 2003 С. 131–132.
24. Баравалле, Х. В. (1948). «Геометрия пятиугольника и золотого сечения». Учитель математики. 41: 22–31.
25. Ливио 2003, п. 141.
26. Шрайбер, Питер (1995). «Приложение к статье Дж. Шаллита» Истоки анализа алгоритма Евклида"". Historia Mathematica. 22 (4): 422–424. Дои:10.1006 / hmat.1995.1033.
27. Ливио 2003 С. 151–152.
28. «Золотое сечение». Архив истории математики MacTutor. Получено 2007-09-18.
29. Вайсштейн, Эрик В. «Формула чисел Фибоначчи Бине». MathWorld.
30. Герц-Фишлер, Роджер (1987). Математическая история деления в крайнем и среднем соотношении. Издательство Университета Уилфрида Лорье. ISBN  978-0889201521.
31. Позаментьер, Альфред С.; Леманн, Ингмар (2011). Великолепное золотое сечение. Книги Прометея. п. 8. ISBN  9-781-61614-424-1.
32. Позаментьер, Альфред С.; Леманн, Ингмар (2011). Великолепное золотое сечение. Книги Прометея. п. 285. ISBN  9-781-61614-424-1.
33. Повар, Теодор Андреа (1914). Кривые жизни. Лондон: Констебль и Компания Лтд., Стр. 420.
34. Барр, Марк (1929). «Параметры красоты». Архитектура (Нью-Йорк). Vol. 60. с. 325. Перепечатано: «Параметры красоты». Считать. Vol. 10–11. Международная корпорация бизнес-машин. 1944 г.
35. Ливио 2003, п. 5.
36. Вайсштейн, Эрик В. "Золотое сечение". MathWorld.
37. Гарднер, Мартин (2001). Колоссальная книга математики: классические головоломки, парадоксы и задачи. W.W. Нортон и компания. С. 77, 88. ISBN  978-0393020236.
38. Герлин, Андреа (5 октября 2011 г.). «Шехтман компании Tecnion получил Нобелевскую премию по химии за открытие квазикристаллов». Bloomberg. Архивировано из оригинал 5 декабря 2014 г.. Получено 4 января, 2019.
39. Ярич, Марко В. (2012), Введение в математику квазикристаллов, Elsevier, стр. Икс, ISBN  978-0323159470, Хотя на момент открытия квазикристаллов теория квазипериодических функций была известна почти шестьдесят лет, это была математика апериодических мозаик Пенроуза, в основном разработанная А. Николаас де Брёйн, что обеспечило основное влияние на новое направление.
40. Ливио 2003 С. 203–209.
41. Гольдман, Алан I .; и другие. (1996). «Квазикристаллические материалы». Американский ученый. 84 (3): 230–241.
42. Буссора, Кенза и Мазуз, Сказал: Использование золотого сечения в Великой мечети Кайруана, Nexus Network Journal, т. 6 шт. 1 (весна 2004 г.).
43. Эллиот, Джейсон (2006). Зеркала невидимого: путешествия по Ирану. Макмиллан. С. 277, 284. ISBN  978-0-312-30191-0.
44. Ле Корбюзье, Модулор п. 25, как цитируется у Падована Ричарда, Пропорции: наука, философия, архитектура (1999), стр. 316, Тейлор и Фрэнсис, ISBN  0-419-22780-6
45. Фрингс, Маркус, Золотое сечение в теории архитектуры, Nexus Network Journal т. 4 шт. 1 (зима 2002 г.).
46. Ле Корбюзье, Модулор, п. 35, цитируется у Падована Ричарда, Пропорции: наука, философия, архитектура (1999), стр. 320. Тейлор и Фрэнсис. ISBN  0-419-22780-6: «И в картинах, и в архитектурных решениях используется золотое сечение».
47. Урвин, Саймон. Анализ архитектуры (2003) стр. 154–155, ISBN  0-415-30685-X
48. Ливио 2003 С. 134–135.
49. Харт, Джордж У. (1999). "Многогранники Леонардо да Винчи". Джордж У. Харт. Получено 10 марта, 2019.
50. Ливио, Марио (1 ноября 2002 г.). «Золотое сечение и эстетика». Plus Magazine. Получено 26 ноября, 2018.
51. Кейт Девлин (май 2007 г.). "Миф, который никуда не денется". Получено 26 сентября, 2013. Похоже, что часть процесса становления писателем-математиком состоит в том, чтобы понять, что нельзя ссылаться на золотое сечение, не следуя при первом упоминании фразой, которая выглядит примерно так: «которую древние греки и другие считали обладающей божественными и мистическими свойствами. ' Почти столь же навязчивым является побуждение добавить второй фактоид вроде «Леонардо да Винчи считал, что человеческая форма отображает золотое сечение». Нет ни малейшего доказательства, подтверждающего любое из утверждений, и есть все основания предполагать, что они оба ложны. Тем не менее, оба утверждения, наряду с другими подобными заявлениями, продолжаются.
52. Дональд Э. Симанек. "Фибоначчи Флим-Флам". Архивировано из оригинал 9 января 2010 г.. Получено 9 апреля, 2013.
53. Сальвадор Дали (2008). Измерение Дали: расшифровка разума гения (DVD). Медиа 3.14-TVC-FGSD-IRL-AVRO.
54. Хант, Карла Херндон и Гилки, Сьюзен Никодемус. Обучение математике в блоке С. 44, 47, ISBN  1-883001-51-X
55. Олариу, Агата, Золотое сечение и искусство живописи Доступно онлайн
56. Тосто, Пабло, La composición áurea en las artes plásticas - El número de oro, Librería Hachette, 1969, стр. 134–144.
57. Ян Чихольд. Форма книги, п. 43 Рис. 4. «Рамки идеальных пропорций в средневековой рукописи без нескольких столбцов. Определено Яном Чихольдом в 1953 году. Пропорции страницы 2: 3. Пропорции полей 1: 1: 2: 3, область текста пропорциональна золотому сечению. угол текстовой области также фиксируется диагональю ".
58. Чихольд, Ян (1991). Форма книги. Хартли и Маркс. С. 27–28. ISBN  0-88179-116-4.
59. Джонс, Рональд (1971). «Золотое сечение: замечательная мера». Структурист. 11: 44–52. Кто бы мог заподозрить, например, что пластина переключателя для одиночных выключателей света стандартизирована в виде золотого прямоугольника?
60. Джонсон, Искусство (1999). Знаменитые задачи и их математики. Библиотеки без ограничений. п. 45. ISBN  978-1-56308-446-1. Золотое сечение является стандартной чертой многих современных дизайнов, от открыток и кредитных карт до плакатов и пластин для выключателей света.
61. Стахов и Ольсен, 2009 г., п. 21. «Кредитная карта имеет форму золотого прямоугольника».
62. Кокс, Саймон (2004). Взломать код да Винчи: неавторизованный справочник по фактам, лежащим в основе бестселлера Дэна Брауна. Barnes & Noble Books. п. 62. ISBN  978-0-7607-5931-8. Золотое сечение также возникает в очень неожиданных местах: широкоэкранные телевизоры, открытки, кредитные карты и фотографии обычно соответствуют его пропорциям.
63. Лендваи, Эрне (1971). Бела Барток: анализ его музыки. Лондон: Кан и Аверилл.
64. Ливио 2003, п. 190.
65. Смит, Питер Ф. Динамика восторга: архитектура и эстетика (Нью-Йорк: Рутледж, 2003) с. 83, ISBN  0-415-30010-X
66. Рой Ховат (1983). Дебюсси в пропорции: музыкальный анализ. Издательство Кембриджского университета. ISBN  978-0-521-31145-8.
67. Саймон Трезизе (1994). Дебюсси: La Mer. Издательство Кембриджского университета. п. 53. ISBN  978-0-521-44656-3.
68. "Жемчужные Мастерс Премиум". Pearl Corporation. Архивировано из оригинал 19 декабря 2007 г.. Получено 2 декабря, 2007.
69. "Шкала 833 центов: эксперимент над гармонией ", Huygens-Fokker.org. По состоянию на 1 декабря 2012 г.
70. Ливио 2003, п. 154.
71. Ричард Падован (1999). Пропорции. Тейлор и Фрэнсис. С. 305–306. ISBN  978-0-419-22780-9.
72. Падован, Ричард (2002). «Пропорции: наука, философия, архитектура». Сетевой журнал Nexus. 4 (1): 113–122. Дои:10.1007 / s00004-001-0008-7.
73. Цейзинг, Адольф (1854). Neue Lehre van den Proportionen des meschlischen Körpers. предисловие.
74. «Золотое сечение обнаружено в квантовом мире». Eurekalert.org. 2010-01-07. Получено 2011-10-31.
75. Поммерсхайм, Джеймс Э., Тим К. Маркс и Эрика Л. Флапан, ред. 2010. "Теория чисел: живое введение с доказательствами, приложениями и историями". Джон Уайли и сыновья: 82.
76. Вайсштейн, Эрик В. (2002). «Сопряжение золотого сечения». CRC Краткая энциклопедия математики, второе изданиеС. 1207–1208. CRC Press. ISBN  978-1420035223.
77. Максимум. Хаильперин; Барбара К. Кайзер; Карл В. Найт (1998). Конкретные абстракции: введение в информатику с использованием схем. Brooks / Cole Pub. Co. ISBN  978-0-534-95211-2.
78. Брайан Розел, "Золотая середина"
79. "Диско-шар в космосе". НАСА. 2001-10-09. Получено 2007-04-16.
80. Крис и Пенни. «Сложности и вопросы». Центр математики. Получено 23 октября 2011.
81. Американский математический ежемесячный журнал, 1954, с. 49–50.
82. Герц-Фишлер, Роджер (2000). Форма Великой пирамиды. Издательство Университета Уилфрида Лорье. ISBN  978-0-88920-324-2.^{[страница нужна ]}
83. Коджа, Мехмет; Коджа, Назифе Оздес; Коч, Рамазан (2010), «Каталонские твердые тела, полученные из трехмерных корневых систем и кватернионов», Журнал математической физики, 51 (4): 043501, arXiv:0908.3272, Bibcode:2010JMP .... 51d3501K, Дои:10.1063/1.3356985, S2CID  115157829.
84. Таттерсолл, Джеймс Джозеф (2005). Элементарная теория чисел в девяти главах (2-е изд.). Издательство Кембриджского университета. п. 28. ISBN  978-0-521-85014-8.
85. Числа Фибоначчи и природа - Часть 2: Почему золотое сечение является «лучшим» расположением?, из Доктора Рона Нотта Числа Фибоначчи и золотое сечение, получено 29 ноября 2012.
86. Вайсштейн, Эрик В. «Число Писо». MathWorld.
87. Horocycles exinscrits: une propriété hyperbolique remarquable, cabri.net, получено 21 июля 2009 г.
88. Brendt, B. et al. «Непрерывная дробь Роджерса – Рамануджана»
89. Йи, Александр Дж. (17 августа 2015 г.). "Золотое сечение". numberword.org. Независимые вычисления выполнены Роном Уоткинсом и Дастином Киркландом.
90. Элисон, Джим (2006). Никсон, Стив (ред.). Лучшее из Астреи: 17 статей по науке, истории и философии. Веб-радио Astrea. С. 92–93. ISBN  978-1-4259-7040-6.
91. Гика, Матила (1977). Геометрия искусства и жизни. Нью-Йорк: Дувр. С. 22–24. ISBN  978-0486235424.
92. Мидхат Газале, Гномон: от фараонов до фракталов, Princeton Univ. Пресса, 1999 г.
93. Эли Маор, Тригонометрические наслаждения, Princeton Univ. Пресса, 2000
94. Хогбен, Ланселот, Математика на миллион, Лондон: Аллен и Анвин, 1942, стр. 63., цитируется Терези, Дик, Утраченные открытия: древние корни современной науки - от вавилонян до майя, Нью-Йорк: Саймон и Шустер, 2003, стр.56.
95. «Великая пирамида, Великое открытие и Великое совпадение». Архивировано из оригинал на 2014-01-02. Получено 2007-11-25.
96. Герц-Фишлер, Роджер (2000). Форма Великой пирамиды. Издательство Университета Уилфрида Лорье. С. 80–89. ISBN  978-0-88920-324-2.
97. Ливио 2003 С. 55–58.
98. Тейлор, Великая пирамида: зачем она была построена и кто ее построил?, 1859
99. Белл, Эрик Темпл (1940). Развитие математики. Нью-Йорк: Дувр. п. 40. ISBN  978-0486272399.
100. Райс, Майкл, Наследие Египта: архетипы западной цивилизации, 3000–30 гг. До н. Э. п. 24 Рутледж, 2003 г., ISBN  0-415-26876-1
101. С. Гедон, 1957, Начало архитектуры, A.W. Mellon Lectures in the Fine Arts, 457, цитируется у Райса, Майкла, Наследие Египта: архетипы западной цивилизации, 3000–30 гг. До н. Э. п. 24 Рутледж, 2003 г.
102. Марковский, Джордж (январь 1992 г.). «Заблуждения о золотом сечении» (PDF). Журнал математики колледжа. Математическая ассоциация Америки. 23 (1): 2–19. Дои:10.2307/2686193. JSTOR  2686193.
103. Фазан, Стивен (1998). Bodyspace. Лондон: Тейлор и Фрэнсис. ISBN  978-0-7484-0067-6.
104. ван Лаак, Вальтер (2001). Лучшая история нашего мира: Том 1 Вселенная. Ахен: van Laach GmbH.
105. Москович, Иван, Коллекция идейного вдохновителя Ивана Московича: навесной квадрат и другие головоломки, Нью-Йорк: Стерлинг, 2004 г.^{[страница нужна ]}
106. Петерсон, Иварс (1 апреля 2005 г.). "Спирали морских ракушек". Новости науки.
107. Человек, Джон, Гутенберг: как один человек переделал мир словом (2002) стр. 166–167, Wiley, ISBN  0-471-21823-5. «Половина страницы (30,7 × 44,5 см) состояла из двух прямоугольников - всей страницы и ее текстовой области - на основе так называемого« золотого сечения », которое определяет важнейшее соотношение между короткой и длинной сторонами и дает иррациональное число, такое как пи, но в соотношении примерно 5: 8 ".
108. Фехнер, Густав (1876 г.). Vorschule der Ästhetik. Лейпциг: Breitkopf & Härtel. С. 190–202.
109. Ливио 2003, п. 7.
110. Например, Ослер пишет, что «38,2% и 61,8% откатов недавних подъемов или падений являются обычным явлением» в Ослер, Кэрол (2000). «Поддержка сопротивления: технический анализ и обменные курсы в течение дня» (PDF). Обзор экономической политики Федерального резервного банка Нью-Йорка. 6 (2): 53–68.
111. Рой Бэтчелор и Ричард Рамьяр "Магические числа в индексе Доу, "25-й Международный симпозиум по прогнозированию, 2005 г., стр. 13, 31".Ни разу с тех пор, как великан прекрасный день, гиганты не выглядели лучше ", Том Стивенсон, Дейли Телеграф, 10 апреля 2006 г., и «Техническая неисправность», Экономист, 23 сентября 2006 г., оба являются сообщениями популярной прессы об исследованиях Бэтчелора и Рамьяра.
112. Ливио 2003 С. 74–75.
113. Ван Мерсберген, Одри М., "Риторические прототипы в архитектуре: измерение Акрополя с помощью философской полемики", Связь ежеквартально, Vol. 46 № 2, 1998, стр. 194–213.
114. Девлин, Кейт Дж. (2009) [2005]. Математический инстинкт: почему вы математический гений (наряду с лобстерами, птицами, кошками и собаками). Нью-Йорк: Базовые книги. п. 54. ISBN  978-1-56025-672-4.
115. Газале, Мидхат Дж., Гномон: от фараонов до фракталов, Princeton University Press, 1999, стр. 125. ISBN  0-691-00514-1
116. Патрис Футакис, «Строили ли греки по золотому сечению?», Кембриджский археологический журнал, т. 24, № 1, февраль 2014 г., стр. 71–86.
117. Le Salon de la Section d'Or, Октябрь 1912 г., Посреднический центр Помпиду
118. Jeunes Peintres ne vous frappez pas!, La Section d'Or: Numéro spécial consacré à l'Exposition de la "Section d'Or", première année, n ° 1, 9 октября 1912 г., стр. 1–7, Bibliothèque Kandinsky
119. Герберт, Роберт, Неоимпрессионизм, Нью-Йорк: Фонд Соломона Р. Гуггенхайма, 1968 г.^{[страница нужна ]}
120. Ливио 2003, п. 169.
121. Кэмфилд, Уильям А., Хуан Грис и Золотое сечение, Вестник Искусства, 47, вып. 1, март 1965 г., стр. 128–134. 68
122. Грин, Кристофер, Хуан Грис, Художественная галерея Уайтчепел, Лондон, 18 сентября - 29 ноября 1992 г .; Staatsgalerie Stuttgart 18 декабря 1992 года - 14 февраля 1993 года; Rijksmuseum Kröller-Müller, Otterlo, 6 марта - 2 мая 1993 г., Yale University Press, 1992, стр. 37–38, ISBN  0300053746
123. Коттингтон, Дэвид, Кубизм и его истории, Критические перспективы Института Барбера в серии по истории искусства, Критические перспективы в истории искусства, Manchester University Press, 2004, стр. 112, 142, ISBN  0719050049
124. Роджер Аллард, Sur quelques peintre, Les Marches du Sud-Ouest, июнь 1911 г., стр. 57–64. У Марка Антлиффа и Патрисии Лейтен, Читатель кубизма, документы и критика, 1906-1914 гг., Издательство Чикагского университета, 2008 г., стр. 178–191, 330.
125. Було, Шарль, Тайная геометрия художника: исследование композиции в искусстве (1963) стр. 247–248, Harcourt, Brace & World, ISBN  0-87817-259-9
126. Ливио 2003 С. 177–178.

Процитированные работы

• Ливио, Марио (2003) [2002]. Золотое сечение: история Фи, самого удивительного числа в мире (Первая торговая книга в мягкой обложке, ред.). Нью-Йорк: Бродвей Книги. ISBN  978-0-7679-0816-0.
• Стахов Алексей П.; Олсен, Скотт (2009). Математика гармонии: от Евклида до современной математики и информатики. Сингапур: World Scientific Publishing. ISBN  978-981-277-582-5.

дальнейшее чтение

• Докзи, Дьёрдь (2005) [1981]. Сила ограничений: пропорциональные гармонии в природе, искусстве и архитектуре. Бостон: публикации Шамбалы. ISBN  978-1-59030-259-0.
• Хеменуэй, Прия (2005). Божественная пропорция: Фи в искусстве, природе и науке. Нью-Йорк: Стерлинг. ISBN  978-1-4027-3522-6.
• Хантли, Х. Э. (1970). Божественная пропорция: исследование математической красоты. Нью-Йорк: Dover Publications. ISBN  978-0-486-22254-7.
• Джозеф, Джордж Г. (2000) [1991]. Гребень павлина: неевропейские корни математики (Новое изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN  978-0-691-00659-8.
• Сахлквист, Лейф (2008). Кардинальные мировоззрения и золотое сечение: принципы древней космографии и дизайна (3-е изд. Ред.). Чарльстон, Южная Каролина: BookSurge. ISBN  978-1-4196-2157-4.
• Шнайдер, Майкл С. (1994). Руководство для начинающих по построению Вселенной: математические архетипы природы, искусства и науки. Нью-Йорк: HarperCollins. ISBN  978-0-06-016939-8.
• Scimone, Альдо (1997). La Sezione Aurea. Culturale di un leitmotiv della Matematica. Палермо: Sigma Edizioni. ISBN  978-88-7231-025-0.
• Вальзер, Ганс (2001) [Der Goldene Schnitt 1993]. Золотое сечение. Питер Хилтон пер. Вашингтон, округ Колумбия: Математическая ассоциация Америки. ISBN  978-0-88385-534-8.

внешняя ссылка

• "Золотое сечение", Энциклопедия математики, EMS Press, 2001 [1994]
• «Золотое сечение» Майкл Шрайбер, Вольфрам Демонстрационный проект, 2007.
• Вайсштейн, Эрик В. "Золотое сечение". MathWorld.
• Нотт, Рон. "Соотношение золотого сечения: Фи". Информация и деятельность профессора математики.
• Пентаграмма и золотое сечение. Грин, Томас М. Обновлено в июне 2005 г. Архивировано в ноябре 2007 г. Инструкция по геометрии с задачами, которые необходимо решить.
• Миф, который никуда не денется, к Кейт Девлин, отвечая на многочисленные утверждения об использовании золотого сечения в культуре.