Квадратное уровненеие - Quadratic equation

Эта статья посвящена алгебраическим уравнениям второй степени и их решениям. Формулу, используемую для поиска решений таких уравнений, см. Квадратичная формула. О функциях, определяемых полиномами второй степени, см. Квадратичная функция.

В квадратичная формула для корней общего квадратного уравнения

В алгебра, а квадратное уровненеие (от латинский квадратная мышца за "квадрат ") - любое уравнение, которое в стандартной форме может быть преобразовано в

${displaystyle ax^{2}+bx+c=0}$

куда Икс представляет собой неизвестный, и а, б, и c представляют известные числа, где а ≠ 0. Если а = 0, то уравнение имеет вид линейный, не квадратичный, так как нет ${displaystyle ax^{2}}$ срок. Цифры а, б, и c являются коэффициенты уравнения и могут быть выделены, называя их соответственно квадратичный коэффициент, то линейный коэффициент и постоянный или же свободный срок.^[1]

Ценности Икс удовлетворяющие уравнению, называются решения уравнения, и корни или же нули из выражение с левой стороны. У квадратного уравнения не более двух решений. Если нет настоящий решение, есть два сложный решения. Если есть только одно решение, говорят, что это двойной корень. Квадратное уравнение всегда имеет два корня, если включены комплексные корни и двойной корень считается за два. Квадратичное уравнение может быть учтенный в эквивалентное уравнение

${displaystyle ax^{2}+bx+c=a(x-r)(x-s)=0}$

куда р и s решения для Икс. Завершение квадрата на квадратное уравнение в стандартной форме приводит к квадратичная формула, который выражает решения через а, б, и c. Решения проблем, которые можно выразить в терминах квадратных уравнений, были известны еще в 2000 году до нашей эры.

Поскольку квадратное уравнение включает только одно неизвестное, оно называется "одномерный ". Квадратное уравнение содержит только полномочия из Икс которые являются неотрицательными целыми числами, и, следовательно, это полиномиальное уравнение. В частности, это вторая степень полиномиальное уравнение, так как наибольшая степень равна двум.

Решение квадратного уравнения

Рисунок 1. Графики квадратичной функции. у = топор² + bx + c, варьируя каждый коэффициент отдельно, в то время как остальные коэффициенты фиксированы (при значениях а = 1, б = 0, c = 0)

Квадратичное уравнение с настоящий или же сложный коэффициенты имеет два решения, называемых корни. Эти два решения могут быть, а могут и не быть разными, и они могут быть или не быть реальными.

Факторинг по инспекции

Можно выразить квадратное уравнение топор² + bx + c = 0 как продукт (px + q)(rx + s) = 0. В некоторых случаях можно путем простого осмотра определить значения п, q, р, и s которые делают две формы эквивалентными друг другу. Если квадратное уравнение записано во второй форме, то "Свойство нулевого фактора" утверждает, что квадратное уравнение выполняется, если px + q = 0 или же rx + s = 0. Решение этих двух линейных уравнений дает корни квадратичной.

Для большинства студентов факторинг путем осмотра - это первый метод решения квадратных уравнений, с которым они сталкиваются.^{[2]:202–207} Если задано квадратное уравнение в виде Икс² + bx + c = 0, искомая факторизация имеет вид (Икс + q)(Икс + s), и нужно найти два числа q и s что в сумме б и чей продукт c (это иногда называют "правилом Виета"^[3] и связан с Формулы Виета ). В качестве примера, Икс² + 5Икс + 6 факторы как (Икс + 3)(Икс + 2). Более общий случай, когда а не равно 1 может потребовать значительных усилий при поиске и проверке методом проб и ошибок, предполагая, что это вообще может быть учтено путем проверки.

За исключением особых случаев, например, когда б = 0 или же c = 0, факторизация по проверке работает только для квадратных уравнений с рациональными корнями. Это означает, что подавляющее большинство квадратных уравнений, возникающих в практических приложениях, не может быть решено факторизацией путем проверки.^[2]:207

Завершение квадрата

Основная статья: Завершение квадрата

Рисунок 2. Для квадратичная функция у = Икс² − Икс − 2, точки пересечения графика Икс-ось, Икс = −1 и Икс = 2, являются решениями квадратного уравнения Икс² − Икс − 2 = 0.

Процесс завершения квадрата использует алгебраическое тождество

${displaystyle x^{2}+2hx+h^{2}=(x+h)^{2},}$

который представляет собой четко определенный алгоритм который можно использовать для решения любого квадратного уравнения.^[2]:207 Начиная с квадратного уравнения в стандартной форме, топор² + bx + c = 0

1. Разделите каждую сторону на а, коэффициент при квадрате члена.
2. Вычтите постоянный член c/а с обеих сторон.
3. Добавьте квадрат половины б/а, коэффициент Икс, в обе стороны. Это «завершает квадрат», превращая левую часть в идеальный квадрат.
4. Запишите левую часть в виде квадрата и при необходимости упростите правую.
5. Получите два линейных уравнения, приравняв квадратный корень из левой части к положительным и отрицательным квадратным корням из правой части.
6. Решите каждое из двух линейных уравнений.

Мы проиллюстрируем использование этого алгоритма, решив 2Икс² + 4Икс − 4 = 0

${displaystyle 1) x^{2}+2x-2=0}$

${displaystyle 2) x^{2}+2x=2}$

${displaystyle 3) x^{2}+2x+1=2+1}$

${displaystyle 4) left(x+1ight)^{2}=3}$

${displaystyle 5) x+1=pm {sqrt {3}}}$

${displaystyle 6) x=-1pm {sqrt {3}}}$

В знак плюс-минус "±" указывает, что оба Икс = −1 + √3 и Икс = −1 − √3 являются решениями квадратного уравнения.^[4]

Квадратичная формула и ее вывод

Основная статья: Квадратичная формула

Завершение квадрата можно использовать для вывести общую формулу для решения квадратных уравнений, называемых квадратной формулой.^[5] В математическое доказательство теперь будут кратко резюмированы.^[6] Это легко увидеть, если полиномиальное разложение, что следующее уравнение эквивалентно квадратному уравнению:

${displaystyle left(x+{frac {b}{2a}}ight)^{2}={frac {b^{2}-4ac}{4a^{2}}}.}$

Принимая квадратный корень с обеих сторон и изолирующий Икс, дает:

${displaystyle x={frac {-bpm {sqrt {b^{2}-4ac}}}{2a}}.}$

Некоторые источники, особенно старые, используют альтернативные параметризации квадратного уравнения, такие как топор² + 2bx + c = 0 или же топор² − 2bx + c = 0 ,^[7] куда б имеет величину, равную половине более распространенной, возможно, с противоположным знаком. Это приводит к несколько разным формам решения, но в остальном они эквивалентны.

Номер альтернативные производные можно найти в литературе. Эти доказательства проще, чем стандартное завершение метода квадратов, представляют интересные приложения других часто используемых методов в алгебре или предлагают понимание других областей математики.

Менее известная квадратичная формула, используемая в Метод Мюллера дает те же корни через уравнение

${displaystyle x={frac {2c}{-bpm {sqrt {b^{2}-4ac}}}}.}$

Это можно вывести из стандартной формулы квадратичных уравнений следующим образом: Формулы Виета, которые утверждают, что продукт корней c/а.

Одним из свойств этой формы является то, что она дает один действительный корень, когда а = 0, а другой корень содержит деление на ноль, потому что когда а = 0, квадратное уравнение превращается в линейное уравнение с одним корнем. Напротив, в этом случае более распространенная формула имеет деление на ноль для одного корня и неопределенная форма 0/0 для другого корня. С другой стороны, когда c = 0, более распространенная формула дает два правильных корня, тогда как эта форма дает нулевой корень и неопределенную форму 0/0.

Приведенное квадратное уравнение

Иногда бывает удобно сократить квадратное уравнение так, чтобы его ведущий коэффициент является одним. Это делается путем разделения обеих сторон на а, что всегда возможно, так как а не равно нулю. Это производит приведенное квадратное уравнение:^[8]

${displaystyle x^{2}+px+q=0,}$

куда п = б/а и q = c/а. Этот моническое уравнение имеет те же решения, что и оригинал.

Квадратичная формула для решений приведенного квадратного уравнения, записанная через его коэффициенты, имеет следующий вид:

${displaystyle x={frac {1}{2}}left(-ppm {sqrt {p^{2}-4q}}ight),}$

или эквивалентно:

${displaystyle x=-{frac {p}{2}}pm {sqrt {left({frac {p}{2}}ight)^{2}-q}}.}$

Дискриминантный

Рисунок 3. Дискриминантные признаки

В формуле квадратного корня выражение под знаком квадратного корня называется выражением дискриминант квадратного уравнения, и часто представляется в верхнем регистре D или греческий верхний регистр дельта:^[9]

${displaystyle Delta =b^{2}-4ac.}$

Квадратичное уравнение с настоящий коэффициенты могут иметь один или два различных действительных корня или два различных комплексных корня. В этом случае дискриминант определяет количество и характер корней. Есть три случая:

• Если дискриминант положительный, то есть два различных корня

${displaystyle {frac {-b+{sqrt {Delta }}}{2a}}quad { ext{and}}quad {frac {-b-{sqrt {Delta }}}{2a}},}$

оба являются действительными числами. Для квадратных уравнений с рациональный коэффициентов, если дискриминант квадратный номер, то корни рациональны - в других случаях они могут быть квадратичные иррациональные числа.

• Если дискриминант равен нулю, то существует ровно один настоящий корень

${displaystyle -{frac {b}{2a}},}$

иногда называется повторным или двойной корень.

• Если дискриминант отрицательный, то реальных корней нет. Скорее, есть два разных (нереальных) сложный корни^[10]

${displaystyle -{frac {b}{2a}}+i{frac {sqrt {-Delta }}{2a}}quad { ext{and}}quad -{frac {b}{2a}}-i{frac {sqrt {-Delta }}{2a}},}$

которые комплексные конъюгаты друг друга. В этих выражениях я это мнимая единица.

Таким образом, корни различны тогда и только тогда, когда дискриминант не равен нулю, а корни действительны тогда и только тогда, когда дискриминант неотрицателен.

Геометрическая интерпретация

График у = топор² + bx + c, куда а и дискриминант б² − 4ac положительные, с

• Корни и у-перехват в красный
• Вершина и ось симметрии в синий
• Фокус и директриса в розовый

Визуализация сложных корней у = топор² + bx + c: парабола поворачивается на 180 ° вокруг своей вершины (апельсин). Его Икс-перехваты поворачиваются на 90 ° вокруг своей средней точки, а декартова плоскость интерпретируется как комплексная плоскость (зеленый).^[11]

Функция ж(Икс) = топор² + bx + c это квадратичная функция.^[12] График любой квадратичной функции имеет одинаковую общую форму, которая называется парабола. Расположение и размер параболы, а также то, как она открывается, зависят от значений а, б, и c. Как показано на рисунке 1, если а > 0, парабола имеет точку минимума и открывается вверх. Если а < 0, парабола имеет максимальную точку и открывается вниз. Крайняя точка параболы, будь то минимум или максимум, соответствует ее вершина. В Икс-координат вершины будет располагаться в ${displaystyle scriptstyle x={ frac {-b}{2a}}}$, а у-координат вершины можно найти, подставив это Икс-ценить в функцию. В у-перехват находится в точке (0, c).

Решения квадратного уравнения топор² + bx + c = 0 соответствуют корни функции ж(Икс) = топор² + bx + c, поскольку они являются значениями Икс для которого ж(Икс) = 0. Как показано на рисунке 2, если а, б, и c находятся действительные числа и домен из ж - множество действительных чисел, то корни ж точно Икс-координаты точек касания графика Икс-ось. Как показано на рисунке 3, если дискриминант положительный, график касается Икс-ось в двух точках; если ноль, график касается в одной точке; а если отрицательный, график не касается Икс-ось.

Квадратичная факторизация

Период, термин

${displaystyle x-r}$

является множителем полинома

${displaystyle ax^{2}+bx+c}$

если и только если р это корень квадратного уравнения

${displaystyle ax^{2}+bx+c=0.}$

Из формулы корней квадратного уравнения следует, что

${displaystyle ax^{2}+bx+c=aleft(x-{frac {-b+{sqrt {b^{2}-4ac}}}{2a}}ight)left(x-{frac {-b-{sqrt {b^{2}-4ac}}}{2a}}ight).}$

В частном случае б² = 4ac где у квадратичной есть только один отличный корень (т.е. дискриминант равен нулю), квадратичный многочлен может быть учтенный в качестве

${displaystyle ax^{2}+bx+c=aleft(x+{frac {b}{2a}}ight)^{2}.}$

Графическое решение

Рис. 4. Графический калькулятор вычисления одного из двух корней квадратного уравнения. 2Икс² + 4Икс − 4 = 0. Хотя на дисплее отображается только пять значащих цифр точности, полученное значение xc составляет 0,732050807569 с точностью до двенадцати значащих цифр.

Квадратичная функция без действительного корня: у = (Икс − 5)² + 9. "3" - это мнимая часть Икс-перехват. Настоящая часть - это Икс-координата вершины. Таким образом, корни 5 ± 3я.

Решения квадратного уравнения

${displaystyle ax^{2}+bx+c=0}$

может быть выведено из график из квадратичная функция

${displaystyle y=ax^{2}+bx+c,}$

который является парабола.

Если парабола пересекает Икс-оси в двух точках, есть две реальные корни, которые являются Икс-координаты этих двух точек (также называемых Икс-перехват).

Если парабола касательная к Икс-оси есть двойной корень, который является Икс-координата точки соприкосновения графика и параболы.

Если парабола не пересекает Икс-оси, есть два комплексно сопряженный корни. Хотя эти корни нельзя визуализировать на графике, их реальные и мнимые части возможно.^[13]

Позволять час и k быть соответственно Икс-координат и у-координата вершины параболы (то есть точки с максимальным или минимальным у-координат. Квадратичную функцию можно переписать

${displaystyle y=a(x-h)^{2}+k.}$

Позволять d быть расстоянием между точкой у-координат 2k на оси параболы, и точка на параболе с тем же у-координата (см. рисунок; таких точек две, которые дают одинаковое расстояние из-за симметрии параболы). Тогда действительная часть корней равна час, а их мнимая часть равна ±d. То есть корни

${displaystyle h+idquad { ext{and}}quad x-id,}$

или в случае примера рисунка

${displaystyle 5+3iquad { ext{and}}quad 5-3i.}$

Как избежать потери значимости

Хотя квадратная формула дает точное решение, результат не точен, если действительные числа аппроксимируются при вычислении, как обычно в числовой анализ, где действительные числа аппроксимируются числа с плавающей запятой (во многих языки программирования ). В этом контексте квадратичная формула не является полностью стабильный.

Это происходит, когда корни имеют разные порядок величины, или, что то же самое, когда б² и б² − 4ac близки по величине. В этом случае вычитание двух почти равных чисел приведет к потеря значимости или же катастрофическая отмена в меньшем корне. Чтобы избежать этого, корень меньшего размера, р, можно вычислить как ${displaystyle (c/a)/R}$ куда р корень, который больше по величине.

Вторая форма отмены может произойти между условиями б² и 4ac дискриминанта, то есть когда два корня очень близки. Это может привести к потере до половины правильных значащих цифр в корнях.^[7][14]

Примеры и приложения

Траектория прыжка с утеса параболический потому что горизонтальное смещение является линейной функцией времени ${displaystyle x=v_{x}t}$, а вертикальное смещение - квадратичная функция времени ${displaystyle y={ frac {1}{2}}at^{2}+v_{y}t+h}$. В результате путь следует квадратному уравнению ${displaystyle y={ frac {a}{2v_{x}^{2}}}x^{2}+{ frac {v_{y}}{v_{x}}}x+h}$, куда ${displaystyle v_{x}}$ и ${displaystyle v_{y}}$ - горизонтальная и вертикальная составляющие исходной скорости, а является гравитационный ускорение и час оригинальная высота. В а значение здесь следует считать отрицательным, так как его направление (вниз) противоположно измерению высоты (вверх).

В Золотое сечение находится как положительное решение квадратного уравнения ${displaystyle x^{2}-x-1=0.}$

Уравнения круг и другие конические секции —эллипсы, параболы, и гиперболы - квадратные уравнения с двумя переменными.

Учитывая косинус или же синус угла, нахождение косинуса или синуса угол, который вдвое меньше включает решение квадратного уравнения.

Процесс упрощения выражений с участием квадратный корень из выражения, включающего квадратный корень из другого выражения включает в себя поиск двух решений квадратного уравнения.

Теорема Декарта утверждает, что для каждых четырех кругов поцелуев (касающихся друг друга) их радиусы удовлетворяют конкретному квадратному уравнению.

Уравнение, данное Теорема Фусса, задавая соотношение между радиусами двухцентровый четырехугольник с вписанный круг, радиус его описанный круг, и расстояние между центрами этих окружностей, может быть выражено в виде квадратного уравнения, для которого расстояние между центрами двух окружностей через их радиусы является одним из решений. Другое решение того же уравнения в терминах соответствующих радиусов дает расстояние между центром описанной окружности и центром окружности. внеокружность из эксантангенциальный четырехугольник.

История

Вавилонские математики, еще в 2000 г. до н.э. (отображено на Старый вавилонский глиняные таблички ) может решить проблемы, связанные с областями и сторонами прямоугольников. Есть свидетельства того, что этот алгоритм датируется еще Третья династия Ура.^[15] В современных обозначениях проблемы обычно включали решение пары одновременных уравнений вида:

${displaystyle x+y=p, xy=q,}$

что эквивалентно утверждению, что Икс и у являются корнями уравнения:^[16]:86

${displaystyle z^{2}+q=pz.}$

Шаги, данные вавилонскими писцами для решения вышеуказанной проблемы прямоугольника с точки зрения Икс и у, были следующие:

1. Вычислить половину п.
2. Возведите результат в квадрат.
3. Вычесть q.
4. Найдите (положительный) квадратный корень, используя таблицу квадратов.
5. Сложите результаты шагов (1) и (4), чтобы получить Икс.

В современных обозначениях это означает вычисление ${displaystyle x=left({frac {p}{2}}ight)+{sqrt {left({frac {p}{2}}ight)^{2}-q}}}$, что эквивалентно современному дню квадратичная формула для большего действительного корня (если есть) ${displaystyle x={frac {-b+{sqrt {b^{2}-4ac}}}{2a}}}$ с а = 1, б = −п, и c = q.

Геометрические методы использовались для решения квадратных уравнений в Вавилонии, Египте, Греции, Китае и Индии. Египетский Берлинский папирус, начиная с Поднебесная (2050 г. до н.э. - 1650 г. до н.э.), содержит решение двухчленного квадратного уравнения.^[17] Вавилонские математики примерно 400 г. до н.э. и Китайские математики примерно с 200 г. до н.э. использовались геометрические методы рассечения решать квадратные уравнения с положительными корнями.^[18][19] Правила для квадратных уравнений приведены в Девять глав математического искусства, китайский трактат по математике.^[19][20] Эти ранние геометрические методы, похоже, не имели общей формулы. Евклид, то Греческий математик, около 300 г. до н.э. создал более абстрактный геометрический метод. С чисто геометрическим подходом Пифагор и Евклид создали общую процедуру для поиска решений квадратного уравнения. В своей работе Арифметика, греческий математик Диофант решает квадратное уравнение, но дает только один корень, даже если оба корня положительны.^[21]

В 628 году нашей эры Брахмагупта, Индийский математик, дала первое явное (хотя и не совсем общее) решение квадратного уравнения топор² + bx = c следующим образом: "К абсолютному числу, умноженному на [коэффициент при] квадрате в четыре раза, прибавьте квадрат [коэффициента] среднего члена; квадратный корень из того же числа за вычетом [коэффициента] среднего члена, деление на дважды [коэффициент] квадрата и есть значение ". (Брахмаспхутасиддханта, Перевод Коулбрука, 1817, стр. 346)^[16]:87 Это эквивалентно:

${displaystyle x={frac {{sqrt {4ac+b^{2}}}-b}{2a}}.}$

В Бахшалинская рукопись написанный в Индии в VII веке нашей эры, содержал алгебраическую формулу для решения квадратных уравнений, а также квадратную формулу. неопределенные уравнения (первоначально типа топор/c = у^{[требуется разъяснение : это линейный, а не квадратичный]}). Мухаммад ибн Муса аль-Хорезми (Персия, 9 век), вдохновленный Брахмагуптой,^{[оригинальное исследование? ]} разработал набор формул, которые работают для положительных решений. Аль-Хорезми идет дальше в предоставлении полного решения общего квадратного уравнения, принимая один или два числовых ответа на каждое квадратное уравнение, обеспечивая при этом геометрическое доказательства в процессе.^[22] Он также описал метод завершения квадрата и признал, что дискриминант должен быть положительным,^[22][23]:230 что было доказано его современником 'Абд аль-Хамид ибн Тюрк (Средняя Азия, IX век), который привел геометрические фигуры, чтобы доказать, что при отрицательном дискриминанте квадратное уравнение не имеет решения.^[23]:234 Хотя сам аль-Хорезми не принимал отрицательных решений, позже Исламские математики его сменившие принимали отрицательные решения,^[22]:191 а также иррациональные числа как решения.^[24] Абу Камил Шуджа ибн Аслам (Египет, 10 век), в частности, был первым, кто принял иррациональные числа (часто в форме квадратный корень, кубический корень или же четвертый корень ) как решения квадратных уравнений или как коэффициенты в уравнении.^[25] Индийский математик 9 века Шридхара записал правила решения квадратных уравнений.^[26]

Еврейский математик Авраам бар Хийя Ха-Наси (XII век, Испания) является автором первой европейской книги, включающей полное решение общего квадратного уравнения.^[27] Его решение было во многом основано на работе Аль-Хорезми.^[22] Письмо китайского математика Ян Хуэй (1238–1298 гг. Н.э.) - первое известное уравнение, в котором появляются квадратные уравнения с отрицательными коэффициентами при «х», хотя он приписывает это более раннему Лю И.^[28] К 1545 году Джероламо Кардано собраны работы, связанные с квадратными уравнениями. Квадратичная формула, охватывающая все случаи, была впервые получена Саймон Стевин в 1594 г.^[29] В 1637 г. Рене Декарт опубликовано La Géométrie содержащую квадратную формулу в том виде, который мы знаем сегодня.

Дополнительные темы

Альтернативные методы расчета корня

Формулы Виета

Основная статья: Формулы Виета

Рисунок 5. График разницы между приближением Виета для меньшего из двух корней квадратного уравнения. Икс² + bx + c = 0 по сравнению со значением, рассчитанным по формуле корней квадратного уравнения. Приближение Виета неточно для малых б но подходит для больших б. Прямая оценка с использованием квадратной формулы точна для малых б с корнями сопоставимого значения, но имеет ошибки потери значимости для больших б и широко расставленные корни.Разница между приближением Виета против прямое вычисление достигает минимума в больших точках, а округление вызывает волнистые линии на кривых за пределами этого минимума.

Формулы Виета дают простую связь между корнями многочлена и его коэффициентами. В случае квадратичного полинома они принимают следующий вид:

${displaystyle x_{1}+x_{2}=-{frac {b}{a}}}$

и

${displaystyle x_{1}x_{2}={frac {c}{a}}.}$

Эти результаты немедленно следуют из соотношения:

${displaystyle left(x-x_{1}ight)left(x-x_{2}ight)=x^{2}-left(x_{1}+x_{2}ight)x+x_{1}x_{2}=0,}$

который можно почленно сравнить с

${displaystyle x^{2}+(b/a)x+c/a=0.}$

Первая формула выше дает удобное выражение для построения графика квадратичной функции. Поскольку график симметричен относительно вертикальной линии, проходящей через вершина, когда есть два действительных корня, вершина Икс-координата расположена на среднем уровне корней (или пересечений). Таким образом Икс-координата вершины задается выражением

${displaystyle x_{V}={frac {x_{1}+x_{2}}{2}}=-{frac {b}{2a}}.}$

В у-координата может быть получена путем подстановки приведенного выше результата в данное квадратное уравнение, что дает

${displaystyle y_{V}=-{frac {b^{2}}{4a}}+c=-{frac {b^{2}-4ac}{4a}}.}$

На практике формулы Виета представляют собой полезный метод нахождения корней квадратичного уравнения в случае, когда один корень намного меньше другого. Если | Икс ₂| << | Икс ₁|, тогда Икс ₁ + Икс ₂ ≈ Икс ₁, и имеем оценку:

${displaystyle x_{1}approx -{frac {b}{a}}.}$

Вторая формула Виета дает:

${displaystyle x_{2}={frac {c}{ax_{1}}}approx -{frac {c}{b}}.}$

Эти формулы намного легче вычислить, чем квадратную формулу при условии одного большого и одного малого корня, потому что квадратная формула оценивает малый корень как разность двух почти равных чисел (случай большого б), что приводит к ошибка округления в числовой оценке. На рисунке 5 показана разница между (i) прямой оценкой с использованием квадратной формулы (точной, когда корни близки друг к другу по значению) и (ii) оценкой, основанной на приведенной выше аппроксимации формул Виета (точной, когда корни широко разнесены. ). Поскольку линейный коэффициент б увеличивается, первоначально квадратичная формула является точной, а приближенная формула становится точнее, что приводит к меньшей разнице между методами, поскольку б увеличивается. Однако в какой-то момент квадратичная формула начинает терять точность из-за ошибки округления, а приближенный метод продолжает совершенствоваться. Следовательно, разница между методами начинает увеличиваться по мере того, как квадратная формула становится все хуже и хуже.

Эта ситуация обычно возникает при проектировании усилителя, когда желательно широко разделенные корни для обеспечения стабильной работы (см. пошаговая реакция ).

Тригонометрическое решение

До появления калькуляторов люди использовали математические таблицы - списки чисел, показывающие результаты вычислений с различными аргументами - для упрощения и ускорения вычислений. Таблицы логарифмов и тригонометрических функций были обычным явлением в учебниках математики и естествознания. Были опубликованы специализированные таблицы для таких приложений, как астрономия, астрономия и статистика. Существовали методы численной аппроксимации, получившие название протокаферез, который предлагал ярлыки для трудоемких операций, таких как умножение и получение степеней и корней.^[30] Астрономов особенно интересовали методы, которые могли бы ускорить длинную серию вычислений, связанных с небесная механика расчеты.

Именно в этом контексте мы можем понять развитие средств решения квадратных уравнений с помощью тригонометрической подстановки. Рассмотрим следующую альтернативную форму квадратного уравнения:

[1]   ${displaystyle ax^{2}+bxpm c=0,}$

где знак символа ± выбран так, чтобы а и c оба могут быть положительными. Подставив

[2]   ${displaystyle x={sqrt {c/a}} an heta }$

а затем умножая на потому что²θ, мы получаем

[3]   ${displaystyle sin ^{2} heta +{frac {b}{sqrt {ac}}}sin heta cos heta pm cos ^{2} heta =0.}$

Представляя функции 2θ и переставляя, получаем

[4]   ${displaystyle an 2 heta _{n}=+2{frac {sqrt {ac}}{b}},}$

[5]   ${displaystyle sin 2 heta _{p}=-2{frac {sqrt {ac}}{b}},}$

где индексы п и п соответствуют, соответственно, использованию отрицательного или положительного знака в уравнении [1]. Подставляя два значения θ_п или же θ_п найдено из уравнений [4] или же [5] в [2] дает необходимые корни [1]. Комплексные корни встречаются в решении, основанном на уравнении [5] если абсолютное значение грех 2θ_п превышает единицу. Объем усилий, затраченных на решение квадратных уравнений с использованием этой смешанной тригонометрической и логарифмической стратегии поиска по таблицам, составлял две трети усилий с использованием одних только логарифмических таблиц.^[31] Для вычисления комплексных корней потребуется использовать другую тригонометрическую форму.^[32]

Для иллюстрации предположим, что у нас есть доступные семизначные логарифмы и тригонометрические таблицы, и мы хотим решить следующую задачу с точностью до шести значащих цифр:

${displaystyle 4.16130x^{2}+9.15933x-11.4207=0}$

1. В поисковой таблице с семью разрядами может быть всего 100 000 записей, и вычисление промежуточных результатов для семи позиций обычно требует интерполяции между соседними записями.
2. ${displaystyle log a=0.6192290,log b=0.9618637,log c=1.0576927}$
3. ${displaystyle 2{sqrt {ac}}/b=2 imes 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314}$
4. ${displaystyle heta =( an ^{-1}1.505314)/2=28.20169^{circ }{ ext{ or }}-61.79831^{circ }}$
5. ${displaystyle log | an heta |=-0.2706462{ ext{ or }}0.2706462}$
6. ${displaystyle log {sqrt {c/a}}=(1.0576927-0.6192290)/2=0.2192318}$
7. ${displaystyle x_{1}=10^{0.2192318-0.2706462}=0.888353}$ (округлено до шести значащих цифр)

${displaystyle x_{2}=-10^{0.2192318+0.2706462}=-3.08943}$

Решение для сложных корней в полярных координатах

Если квадратное уравнение ${displaystyle ax^{2}+bx+c=0}$ с действительными коэффициентами имеет два комплексных корня - случай, когда ${displaystyle b^{2}-4ac<0,}$ требующий а и c иметь одинаковый знак друг с другом - тогда решения для корней можно выразить в полярной форме как^[33]

${displaystyle x_{1},,x_{2}=r(cos heta pm isin heta ),}$

куда ${displaystyle r={sqrt { frac {c}{a}}}}$ и ${displaystyle heta =cos ^{-1}left({ frac {-b}{2{sqrt {ac}}}}ight).}$

Геометрическое решение

Рисунок 6. Геометрическое решение топор² + bx + c = 0 используя метод Лилля. Решения: −AX1 / SA, −AX2 / SA

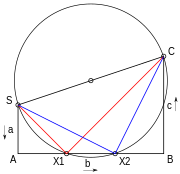
Квадратное уравнение может быть решено геометрически несколькими способами. Один путь - через Метод Лилля. Три коэффициента а, б, c нарисованы с прямыми углами между ними, как в SA, AB и BC на рисунке 6. Нарисована окружность с начальной и конечной точками SC в качестве диаметра. Если это пересекает среднюю линию AB из трех, то уравнение имеет решение, и решения даются как отрицательное значение расстояния вдоль этой линии от A, деленного на первый коэффициент а или SA. Если а является 1 коэффициенты можно считывать напрямую. Таким образом, решения на диаграмме - это −AX1 / SA и −AX2 / SA.^[34]

Круг Карлейля квадратного уравнения Икс² − sx + п = 0.

В Карлайл круг, названный в честь Томас Карлайл, обладает тем свойством, что решения квадратного уравнения являются горизонтальными координатами пересечений окружности с Горизонтальная ось.^[35] Круги Карлайла использовались для разработки линейки-компас конструкции из правильные многоугольники.

Обобщение квадратного уравнения

Формула и ее вывод остаются верными, если коэффициенты а, б и c находятся сложные числа, или, в более общем смысле, члены любого поле чей характеристика не является 2. (В поле характеристики 2 элемент 2а равен нулю и делить на него невозможно.)

Символ

${displaystyle pm {sqrt {b^{2}-4ac}}}$

в формуле следует понимать как «любой из двух элементов, квадрат которых равен б² − 4ac, если такие элементы существуют ". В некоторых полях некоторые элементы не имеют квадратных корней, а некоторые - два; только ноль имеет только один квадратный корень, за исключением полей характеристики 2. Даже если поле не содержит квадратного корня из некоторого числа, всегда есть квадратичный поле расширения что делает, поэтому квадратная формула всегда будет иметь смысл как формула в этом поле расширения.

Характеристика 2

В области характеристик 2, квадратичная формула, основанная на 2 быть единица измерения, не держит. Рассмотрим моник квадратичный многочлен

${displaystyle x^{2}+bx+c}$

над полем характеристики 2. Если б = 0, то решение сводится к извлечению квадратного корня, поэтому решение

${displaystyle x={sqrt {c}}}$

и есть только один корень, так как

${displaystyle -{sqrt {c}}=-{sqrt {c}}+2{sqrt {c}}={sqrt {c}}.}$

В итоге,

${displaystyle displaystyle x^{2}+c=(x+{sqrt {c}})^{2}.}$

Видеть квадратичный вычет для получения дополнительной информации об извлечении квадратных корней в конечных полях.

В случае, если б ≠ 0, есть два различных корня, но если многочлен несводимый, они не могут быть выражены через квадратные корни из чисел в поле коэффициентов. Вместо этого определите 2-корень р(c) из c быть корнем многочлена Икс² + Икс + c, элемент поле расщепления этого полинома. Один подтверждает, что р(c) + 1 тоже корень. В терминах операции с двумя корнями два корня (немонической) квадратичной топор² + bx + c находятся

${displaystyle {frac {b}{a}}Rleft({frac {ac}{b^{2}}}ight)}$

и

${displaystyle {frac {b}{a}}left(Rleft({frac {ac}{b^{2}}}ight)+1ight).}$

Например, пусть а обозначают мультипликативный образующий группы единиц F₄, то Поле Галуа четвертого порядка (таким образом а и а + 1 корни Икс² + Икс + 1 над F₄. Потому что (а + 1)² = а, а + 1 является единственным решением квадратного уравнения Икс² + а = 0. С другой стороны, полином Икс² + топор + 1 неприводимо над F₄, но он разделяется F₁₆, где имеет два корня ab и ab + а, куда б это корень Икс² + Икс + а в F₁₆.

Это частный случай Теория Артина – Шрайера.

Смотрите также

• Решение квадратных уравнений с цепными дробями
• Линейное уравнение
• Кубическая функция
• Уравнение четвертой степени
• Квинтическое уравнение
• Основная теорема алгебры

Рекомендации

1. Проттерс и Морри: «Исчисление и аналитическая геометрия. Первый курс».
2. Вашингтон, Аллин Дж. (2000). Основы технической математики с исчислением, седьмое издание. Addison Wesley Longman, Inc. ISBN  978-0-201-35666-3.
3. Эббингаус, Хайнц-Дитер; Юинг, Джон Х. (1991), Числа, Тексты для выпускников по математике, 123, Springer, стр. 77, ISBN  9780387974972.
4. Стерлинг, Мэри Джейн (2010), Алгебра I для чайников, Wiley Publishing, стр. 219, ISBN  978-0-470-55964-2
5. Рич, Барнетт; Шмидт, Филипп (2004), Очерк теории и проблем элементарной алгебры Шаума, Компании McGraw-Hill, ISBN  978-0-07-141083-0, Глава 13 §4.4, с. 291
6. Химонас, Алекс. Расчет для бизнеса и социальных наук, п. 64 (Публикации Ричарда Денниса, 2001).
7. Кахан, Виллиан (20 ноября 2004 г.), О стоимости вычислений с плавающей запятой без сверхточной арифметики (PDF), получено 2012-12-25
8. Аленицын Александр и Бутиков Евгений. Краткий справочник по математике и физике, п. 38 (CRC Press 1997)
9. Δ это начало Греческий слово Διακρίνουσα, Diakrínousa, дискриминант.
10. Ахатц, Томас; Андерсон, Джон Дж .; Маккензи, Кэтлин (2005). Технический цех математики. Промышленная пресса. п. 277. ISBN  978-0-8311-3086-2.
11. «Сложные корни стали видимыми - забавные математические факты». Получено 1 октября 2016.
12. Уортон, П. (2006). Основы Edexcel Gcse Math / Higher. Лонсдейл. п. 63. ISBN  978-1-905-129-78-2.
13. Алек Нортон, Бенджамин Лото (июнь 1984 г.), «Сложные корни стали видимыми», Математический журнал колледжа, 15 (3): 248–249, Дои:10.2307/2686333, JSTOR  2686333
14. Хайэм, Николас (2002), Точность и стабильность численных алгоритмов (2-е изд.), SIAM, стр. 10, ISBN  978-0-89871-521-7
15. Фриберг, Йоран (2009). "Геометрический алгоритм с решениями квадратных уравнений в шумерском юридическом документе из Ур III Умма". Журнал электронной библиотеки клинописи. 3.
16. Стиллвелл, Джон (2004). Математика и ее история (2-е изд.). Springer. ISBN  978-0-387-95336-6.
17. Кембриджская древняя история, часть 2 Ранняя история Ближнего Востока. Издательство Кембриджского университета. 1971. с. 530. ISBN  978-0-521-07791-0.
18. Хендерсон, Дэвид В. «Геометрические решения квадратных и кубических уравнений». Математический факультет Корнельского университета. Получено 28 апреля 2013.
19. Эйткен, Уэйн. "Китайская классика: девять глав" (PDF). Математический факультет Калифорнийского государственного университета. Получено 28 апреля 2013.
20. Смит, Дэвид Юджин (1958). История математики. Courier Dover Publications. п. 380. ISBN  978-0-486-20430-7.
21. Смит, Дэвид Юджин (1958). История математики, Том 1. Courier Dover Publications. п. 134. ISBN  978-0-486-20429-1. Выдержка страницы 134
22. Кац, В. Дж .; Бартон, Б. (2006). «Этапы истории алгебры с последствиями для обучения». Образовательные исследования по математике. 66 (2): 185–201. Дои:10.1007 / s10649-006-9023-7. S2CID  120363574.
23. Бойер, Карл Б .; Ута К. Мерцбах, ред. редактор (1991). История математики. John Wiley & Sons, Inc. ISBN  978-0-471-54397-8.
24. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Арабская математика: забытый талант?", Архив истории математики MacTutor, Сент-Эндрюсский университет. «Алгебра была объединяющей теорией, которая позволяла рассматривать рациональные числа, иррациональные числа, геометрические величины и т. Д. Как« алгебраические объекты ».
25. Жак Сезиано, "Исламская математика", стр. 148, дюйм Селин, Хелайн; Д'Амброзио, Убиратан, ред. (2000), Математика в разных культурах: история незападной математики, Springer, ISBN  978-1-4020-0260-1
26. Смит, Дэвид Юджин (1958). История математики. Courier Dover Publications. п. 280. ISBN  978-0-486-20429-1.
27. Ливио, Марио (2006). Уравнение, которое не могло быть решено. Саймон и Шустер. ISBN  978-0743258210.
28. Ронан, Колин (1985). Более короткая наука и цивилизация в Китае. Издательство Кембриджского университета. п. 15. ISBN  978-0-521-31536-4.
29. Struik, D. J .; Стевин, Саймон (1958), Основные работы Саймона Стевина по математике (PDF), II – B, C. V. Swets & Zeitlinger, стр. 470
30. Ballew, Pat. «Решение квадратных уравнений - аналитическими и графическими методами; включая несколько методов, которых вы, возможно, никогда не видели» (PDF). Архивировано из оригинал (PDF) 9 апреля 2011 г.. Получено 18 апреля 2013.
31. Сирс, Ф. Х. (1945). «Тригонометрическое решение квадратного уравнения». Публикации Тихоокеанского астрономического общества. 57 (339): 307–309. Bibcode:1945PASP ... 57..307S. Дои:10.1086/125759.
32. Од, Х. Т. Р. (1938). "Решения квадратного уравнения, полученные с помощью тригонометрии". Национальный математический журнал. 13 (3): 118–121. Дои:10.2307/3028750. JSTOR  3028750.
33. Саймонс, Стюарт, "Альтернативный подход к комплексным корням вещественных квадратных уравнений", Математический вестник 93, март 2009 г., стр. 91–92.
34. Биксби, Уильям Герберт (1879), Графический метод быстрого нахождения истинных корней числовых уравнений любой степени, Вест-Пойнт Н. Ю.
35. Вайсштейн, Эрик В. "Карлайл Серкл". Из MathWorld - веб-ресурса Wolfram. Получено 21 мая 2013.

внешняя ссылка

• "Квадратное уровненеие", Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. "Квадратные уравнения". MathWorld.
• 101 использование квадратного уравнения
• 101 использование квадратного уравнения: Часть II