Золотой угол - Golden angle

О бабочке см. Caprona ransonnetii.

Золотой угол - это угол, образуемый меньшей (красной) дугой, когда две дуги, составляющие круг, находятся в Золотое сечение

В геометрия, то золотой угол это меньший из двух углы создается путем разделения окружности круга в соответствии с Золотое сечение; то есть на два дуги так, чтобы отношение длины меньшей дуги к длине большей дуги было таким же, как отношение длины большей дуги к полной длине окружности.

Алгебраически пусть а + б быть окружностью круг, разделенный на более длинную дугу длины а и меньшая дуга длины б такой, что

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}}$

Золотой угол - это угол поданный по меньшей дуге длины б. Он измеряет приблизительно 137,5077640500378546463487 ... ° OEIS: A096627 или в радианы 2.39996322972865332 ... OEIS: A131988.

Название происходит от связи золотого угла с Золотое сечение φ; точное значение золотого угла

${\displaystyle 360\left(1-{\frac {1}{\varphi }}\right)=360(2-\varphi )={\frac {360}{\varphi ^{2}}}=180(3-{\sqrt {5}}){\text{ degrees}}}$

или же

${\displaystyle 2\pi \left(1-{\frac {1}{\varphi }}\right)=2\pi (2-\varphi )={\frac {2\pi }{\varphi ^{2}}}=\pi (3-{\sqrt {5}}){\text{ radians}},}$

где эквивалентности следуют из хорошо известных алгебраических свойств золотого сечения.

Вывод

Золотое сечение равно φ = а/б учитывая вышеуказанные условия.

Позволять ƒ быть частью окружности, образуемой золотым углом, или, что эквивалентно, золотым углом, деленным на угловое измерение круга.

${\displaystyle f={\frac {b}{a+b}}={\frac {1}{1+\varphi }}.}$

Но с тех пор

${\displaystyle {1+\varphi }=\varphi ^{2},}$

следует, что

${\displaystyle f={\frac {1}{\varphi ^{2}}}}$

Это эквивалентно тому, что φ ² золотые углы могут уместиться в круг.

Следовательно, доля круга, занимаемого золотым углом, равна

${\displaystyle f\approx 0.381966.\,}$

Золотой угол грамм поэтому можно численно аппроксимировать градусы в качестве:

${\displaystyle g\approx 360\times 0.381966\approx 137.508^{\circ },\,}$

или в радианах как:

${\displaystyle g\approx 2\pi \times 0.381966\approx 2.39996.\,}$

Золотой угол в природе

Угол между следующими друг за другом цветочками у некоторых цветов - золотой угол.

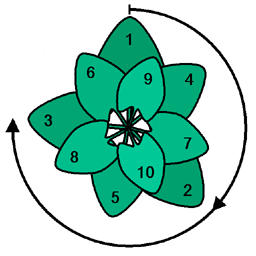
Золотой угол играет значительную роль в теории филлотаксис; например, золотой угол - это угол, разделяющий цветочки на подсолнечник.^[1] Анализ рисунка показывает, что он очень чувствителен к углу, разделяющему человека. примордия, причем угол Фибоначчи дает парастихия с оптимальной плотностью упаковки.^[2]

Математическое моделирование вероятного физического механизма развития цветков показало закономерность, спонтанно возникающую при решении нелинейного уравнения в частных производных на плоскости.^[3][4]

Рекомендации

1. Дженнифер Чу (2011-01-12). "А вот и Солнце". Новости MIT. Получено 2016-04-22.
2. Ридли, Дж. (Февраль 1982 г.). «Эффективность упаковки в головки подсолнечника». Математические биологические науки. 58 (1): 129–139. Дои:10.1016/0025-5564(82)90056-6.
3. Пеннибекер, Мэтью; Ньюэлл, Алан К. (13.06.2013). «Филлотаксис, выдвигающиеся фасады, формирующие узор, и оптимальная упаковка» (PDF). Письма с физическими проверками. 110 (24): 248104. Дои:10.1103 / PhysRevLett.110.248104. ISSN  0031-9007. PMID  25165965.
4. «Подсолнухи и Фибоначчи: модели эффективности». ThatsMaths. 2014-06-05. Получено 2020-05-23.

• Фогель, Х (1979). «Лучший способ построить голову подсолнуха». Математические биологические науки. 44 (3–4): 179–189. Дои:10.1016/0025-5564(79)90080-4.
• Прусинкевич, Пшемыслав; Линденмайер, Аристид (1990). Алгоритмическая красота растений. Springer-Verlag. стр.101–107. ISBN  978-0-387-97297-8.

внешняя ссылка

• Золотой угол в MathWorld