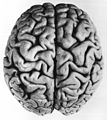
Узоры в природе - Patterns in nature


Узоры в природе видимые закономерности формы, встречающиеся в мире природы. Эти узоры повторяются в разных контекстах и иногда могут быть смоделирован математически. Природные узоры включают симметрии, деревья, спирали, извилины, волны, пены, мозаика, трещины и полосы.[1] Рано Греческие философы изученный образец, с Платон, Пифагор и Эмпедокл пытаясь объяснить порядок в природе. Современное понимание видимых узоров со временем развивалось.
В 19 веке бельгийский физик Плато Джозеф исследовал мыльные фильмы, что привело его к формулированию концепции минимальная поверхность. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морские организмы чтобы подчеркнуть их симметрия. Шотландский биолог Д'Арси Томпсон был пионером в изучении моделей роста как у растений, так и у животных, показав, что простые уравнения могут объяснить спиральный рост. В ХХ веке британский математик Алан Тьюринг предсказанные механизмы морфогенез которые приводят к узоры пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа Мандельброт показал, как математика фракталы может создавать модели роста растений.
Математика, физика и химия может объяснять закономерности в природе на разных уровнях. Образцы в живых существах объясняются биологический процессы естественный отбор и половой отбор. Исследования формирование рисунка использовать компьютерные модели для моделирования широкого спектра узоров.
История

Ранние греческие философы пытались объяснить порядок в природа, предвосхищая современные концепции. Пифагор (ок. 570 – ок. 495 до н. э.) объяснил закономерности в природе, такие как гармонии музыки, как возникающие из числа, которое он считал основной составляющей существования.[а] Эмпедокл (ок. 494 – ок. 434 г. до н. э.) в ожидаемой степени Дарвин Эволюционное объяснение структур организмов.[b] Платон (ок. 427 – ок. 347 до н. э.) доказывал существование естественных универсалии. Он считал, что они состоят из идеальные формы (εἶδος эйдос: "form") физические объекты которых всегда являются несовершенными копиями. Таким образом, цветок может быть примерно круглым, но никогда не бывает идеальным.[2]
Теофраст (ок. 372 – ок. 287 до н. э.) отметил, что растения «с плоскими листьями имеют их в регулярной последовательности»; Плиний Старший (23–79 г. н.э.) отметили их узорчатое круговое расположение.[3] Спустя века Леонардо да Винчи (1452–1519) отметили спиралевидное расположение узоров листьев, что стволы деревьев с возрастом получают последовательные кольца, и предложил правило якобы удовлетворены площадью поперечного сечения ветвей деревьев.[4][3] Иоганн Кеплер (1571–1630) указали на наличие Последовательность Фибоначчи в природе, используя его для объяснения пятиугольник форма некоторых цветов.[3] В 1754 г. Шарль Бонне заметил, что спираль филлотаксис растений часто выражались в обоих по часовой стрелке и против часовой стрелки Золотое сечение серии.[3] Математические наблюдения филлотаксиса сопровождались Карл Фридрих Шимпер и его друг Александр Браун работы 1830 и 1830 годов соответственно; Огюст Браве и его брат Луи соединили отношения филлотаксиса с последовательностью Фибоначчи в 1837 году, также отметив его появление в сосновые шишки и ананасы.[3] В своей книге 1854 года немецкий психолог Адольф Цейзинг исследовали золотое сечение, выраженное в расположении частей растений, скелеты животных и паттерны ветвления их вен и нервов, а также в кристаллы.[5][6][7] А. Х. Чёрч изучал закономерности филлотаксиса в своей книге 1904 года.[8] В 1917 г. Д'Арси Томпсон опубликовано О росте и форме; его описание филлотаксиса и последовательности Фибоначчи, математические соотношения в спиральных моделях роста растений показали, что простые уравнения могут описывать спиральные паттерны роста растений. рога животных и раковины моллюсков.[9]
В 1202 г. Леонардо Фибоначчи представил последовательность Фибоначчи западному миру в своей книге Liber Abaci.[10] Фибоначчи представил мысленный эксперимент о росте идеализированного кролик численность населения.[11]
В 1658 году английский врач и философ Сэр Томас Браун обсуждали "как природа геометризирует" в Сад Кира, цитируя Пифагорейская нумерология с числом 5 и Платоническая форма из квинконс шаблон. Центральная глава дискурса содержит примеры и наблюдения квинконса в ботанике.[12]
Бельгийский физик Плато Джозеф (1801–1883) сформулировал математическая проблема о существовании минимальная поверхность с заданной границей, которая теперь названа его именем. Он интенсивно изучал мыльные пленки, формулируя Законы Плато которые описывают структуры, образованные пленками в пенах.[13]
Эрнст Геккель (1834–1919) нарисовал прекрасные иллюстрации морских организмов, в частности Радиолярии, подчеркивая их симметрия чтобы поддержать его поддельныеДарвиновский теории эволюции.[14]
Американский фотограф Уилсон Бентли сделал первую микрофотографию снежинка в 1885 г.[15]

В 1952 г. Алан Тьюринг (1912–1954), более известный своими работами по вычислительной технике и взлом кода, написал Химические основы морфогенеза, анализ механизмов, которые потребуются для создания паттернов в живых организмах, в процессе, называемом морфогенез.[16] Он предсказал колеблющийся химические реакции, в частности Реакция Белоусова – Жаботинского. Эти механизмы активатор-ингибитор могут, как предположил Тьюринг, генерировать паттерны (названные "Паттерны Тьюринга ") полос и пятен у животных, и вносят вклад в спиральные узоры, наблюдаемые при филлотаксисе растений.[17]
В 1968 году венгерский биолог-теоретик Аристид Линденмайер (1925–1989) разработали L-система, а формальная грамматика который можно использовать для моделирования модели роста растений в стиле фракталы.[18] L-системы имеют алфавит символов, которые можно комбинировать, используя правила производства для построения больших цепочек символов и механизма для преобразования сгенерированных строк в геометрические структуры. В 1975 году, после столетий медленного развития математики закономерностей, Готфрид Лейбниц, Георг Кантор, Хельге фон Кох, Вацлав Серпинский и другие, Бенуа Мандельброт написал известную статью, Какова длина побережья Британии? Статистическое самоподобие и дробная размерность кристаллизации математической мысли в концепцию фрактал.[19]
Причины
Живые существа как орхидеи, колибри, а хвост павлина иметь абстрактный дизайн с красотой формы, узора и цвета, с которыми художники с трудом справляются.[20] Красота, которую люди воспринимают в природе, имеет причины на разных уровнях, в частности, в математике, которая определяет, какие модели могут физически формироваться, и среди живых существ в результате естественного отбора, который определяет эволюцию моделей.[21]
Математика стремится открывать и объяснять абстрактные закономерности или закономерности всех видов.[22][23]Визуальные закономерности в природе находят объяснение в теория хаоса, фракталы, логарифмические спирали, топология и другие математические закономерности. Например, L-системы формировать убедительные модели различных закономерностей роста деревьев.[18]
Законы физика применять абстракции математики к реальному миру, часто как если бы идеально. Например, кристалл идеален, когда он не имеет структурных дефектов, таких как дислокации, и полностью симметричен. Точное математическое совершенство может только приблизиться к реальным объектам.[24] Видимые закономерности в природе регулируются физические законы; Например, извилины можно объяснить с помощью динамика жидкостей.
В биология, естественный отбор может вызывать развитие закономерностей в живых существах по нескольким причинам, в том числе камуфляж,[25] половой отбор,[25] и различные виды сигнализации, в том числе мимикрия[26] и чистящий симбиоз.[27] У растений формы, цвета и узоры опыляемый насекомыми цветы словно Лили эволюционировали, чтобы привлекать насекомых, таких как пчелы. Радиальные узоры цветов и полос, некоторые из которых видны только в ультрафиолетовом свете, служат проводники нектара что видно на расстоянии.[28]
Виды выкройки
Симметрия
Симметрия широко распространено в живых существах. Животные в основном имеют двустороннюю или зеркальная симметрия, как и листья растений и некоторые цветы, такие как орхидеи.[29] Растения часто имеют радиальные или вращательная симметрия, как и многие цветы и некоторые группы животных, такие как морские анемоны. Пятикратная симметрия обнаружена в иглокожие, группа, в которую входят морская звезда, морские ежи, и морские лилии.[30]
Среди неживых существ, снежинки иметь поразительный шестикратная симметрия; Структура каждой чешуйки представляет собой запись различных условий во время ее кристаллизации, с почти одинаковым рисунком роста на каждом из шести ее плеч.[31] Кристаллы в целом имеют различные симметрии и кристальные привычки; они могут быть кубическими или октаэдрическими, но настоящие кристаллы не могут иметь пятикратную симметрию (в отличие от квазикристаллы ).[32] Вращательная симметрия встречается в разных масштабах у неживых существ, включая коронообразную всплеск узор, образующийся при падении капли в пруд,[33] и оба сфероидальный форма и кольца планета подобно Сатурн.[34]
Симметрия имеет множество причин. Радиальная симметрия подходит таким организмам, как морские анемоны, взрослые особи которых не двигаются: пища и угрозы могут прибывать с любого направления. Но животные, которые движутся в одном направлении, обязательно имеют верхнюю и нижнюю стороны, концы головы и хвоста, а значит, левую и правую. Голова приобретает особую форму рта и органов чувств (цефализация ), и тело становится двусторонне симметричным (хотя внутренние органы могут быть не такими).[35] Более загадочной является причина пятичастной (пятиугольной) симметрии иглокожих. Ранние иглокожие были билатерально симметричны, как и их личинки. Самралл и Рэй утверждают, что потеря старой симметрии имела как связанные с развитием, так и экологические причины.[36]

Животные часто показывают зеркало или двусторонняя симметрия, так тигр.

Иглокожие так морская звезда имеют пятеричная симметрия.

Пятикратную симметрию можно увидеть во многих цветках и некоторых фруктах, подобных этому. мушмула.

Снежинки имеют шестикратная симметрия.

Флюорит показывая кубический кристальная привычка.

Вода всплеск приблизительно радиальная симметрия.

Гранат показывает габитус ромбического додекаэдра.

Volvox имеет сферическую симметрию.
Деревья, фракталы
Схема ветвления деревьев описана в Итальянский ренессанс к Леонардо да Винчи. Он заявил, что:
Все ветви дерева на каждой стадии его роста, когда собраны вместе, равны по толщине стволу [под ними].[37]
Более общая версия гласит, что когда родительская ветвь разделяется на две или более дочерних ветвей, площадь поверхности дочерних ветвей складывается с площадями родительской ветки.[38] Эквивалентная формулировка состоит в том, что если родительская ветвь разделяется на две дочерние ветви, то диаметры поперечного сечения родительской и двух дочерних ветвей образуют прямоугольный треугольник. Одно из объяснений состоит в том, что это позволяет деревьям лучше противостоять сильным ветрам.[38] Моделирование биомеханических моделей согласуется с правилом.[39]
Фракталы бесконечно самоподобный, повторные математические конструкции, имеющие фрактальная размерность.[19][40][41] Бесконечный итерация невозможно в природе, поэтому все «фрактальные» паттерны являются приблизительными. Например, листья папоротники и зонтичные (Apiaceae) самоподобны (перистые) только на 2, 3 или 4 уровнях. Паттерны роста, похожие на папоротник, встречаются у растений и животных, включая мшанки, кораллы, гидрозоа словно воздушный папоротник, Sertularia argentea, и в неживых существах, особенно электрические разряды. Система Линденмайера фракталы могут моделировать различные модели роста деревьев, изменяя небольшое количество параметров, включая угол ветвления, расстояние между узлами или точками ветвления (междоузлия длина), и количество ветвей на точку ветвления.[18]
Фрактальные узоры широко распространены в природе в таких разнообразных явлениях, как облака, речные сети, геологический Линии разломов, горы, береговые линии,[42] окраска животных, снежинки,[43] кристаллы,[44] кровеносный сосуд ветвление[45] актиновый цитоскелет,[46] и Океанские волны.[47]

Модели роста некоторых деревьев напоминают эти Система Линденмайера фракталы.

Схема разветвления баобаб дерево

Лист петрушки коровьей, Anthriscus sylvestris, это 2- или 3-перистый, не бесконечно

Фрактал спирали: Романеско брокколи показывая самоподобный форма

Деревья: Фигура Лихтенберга: высокое напряжение диэлектрик поломка в акриловый полимер блокировать

Деревья: дендритный кристаллы меди (в микроскоп)
Спирали
Спирали распространены у растений и некоторых животных, особенно моллюски. Например, в наутилус, головоногий моллюск, каждый камера его оболочки является приблизительной копией следующей, масштабированной с постоянным коэффициентом и расположенной в логарифмическая спираль.[48] Учитывая современное понимание фракталов, спираль роста можно рассматривать как частный случай самоподобия.[49]
Спирали растений можно увидеть в филлотаксис, расположение листьев на стебле и в расположении (парастихия[50]) других частей, как в составной цветочные головки и семенные головки словно подсолнечник или же фрукты структуры, подобные ананас[8][51]:337 и змеиный фрукт, а также в узоре чешуек в сосновые шишки, где несколько спиралей движутся как по часовой, так и против часовой стрелки. У этих договоренностей есть объяснения на разных уровнях - математике, физике, химии, биологии - каждое индивидуально правильное, но все необходимое вместе.[52] Спирали филлотаксиса могут быть получены математически из Отношения Фибоначчи: последовательность Фибоначчи проходит 1, 1, 2, 3, 5, 8, 13 ... (каждое последующее число является суммой двух предыдущих). Например, когда листья чередуются вверх по стеблю, один оборот спирали касается двух листьев, поэтому узор или соотношение равно 1/2. В орешник соотношение 1/3; в абрикос это 2/5; в груша это 3/8; в миндаль это 5/13.[53] В филлотаксисе диска, как в подсолнечник и маргаритка, соцветия расположены в Спираль Ферма с нумерацией Фибоначчи, по крайней мере, когда цветочная головка созрела, поэтому все элементы имеют одинаковый размер. Соотношения Фибоначчи приблизительно равны золотой угол, 137,508 °, что определяет кривизну спирали Ферма.[54]
С точки зрения физики спирали представляют собой конфигурации с наименьшей энергией.[55] которые возникают спонтанно через самоорганизующийся процессы в динамические системы.[56] С точки зрения химии, спираль может быть образована процессом реакции-диффузии, включающим как активацию, так и ингибирование. Филлотаксис контролируется белки которые манипулируют концентрацией растительного гормона ауксин, что активирует меристема рост, наряду с другими механизмами контроля относительного угла почек вокруг стебля.[57] С биологической точки зрения, размещение листьев как можно дальше друг от друга в любом заданном пространстве благоприятствует естественному отбору, поскольку он максимизирует доступ к ресурсам, особенно солнечному свету. фотосинтез.[51]

Фибоначчи спираль

снежный баран, Овис канадский

Спирали: филлотаксис спирального алоэ, Алоэ полифилла

Наутилус оболочки логарифмический спираль роста
Спираль Ферма: семенная головка подсолнечник, Helianthus annuus

Множественные спирали Фибоначчи: красный капуста в поперечном сечении

Спиральная оболочка Trochoidea liebetruti

Капли воды отлетают от мокрого вращающегося шара в равносторонние спирали
Хаос, поток, меандры
В математике динамическая система хаотичен, если он (очень) чувствителен к начальным условиям (так называемый "эффект бабочки "[58]), что требует математических свойств топологическое перемешивание и плотный периодические орбиты.[59]
Наряду с фракталами теория хаоса считается универсальным влиянием на закономерности в природе. Между хаосом и фракталами существует связь - странные аттракторы в хаотических системах есть фрактальная размерность.[60] Немного клеточные автоматы, простые наборы математических правил, которые генерируют закономерности, имеют хаотическое поведение, в частности Стивен Вольфрам с Правило 30.[61]
Вихревые улицы зигзагообразные узоры кружения вихри созданный неустойчивым разделение потока из жидкость, чаще всего воздухом или водой, над препятствующими объектами.[62] Гладкий (ламинарный ) поток начинает разрушаться, когда размер препятствия или скорость потока становятся достаточно большими по сравнению с вязкость жидкости.
Меандры извилистые изгибы рек или других каналов, которые образуются, когда жидкость, чаще всего вода, течет вокруг изгибов. Как только путь немного изогнут, размер и кривизна каждой петли увеличиваются по мере винтовой поток перетаскивает такие материалы, как песок и гравий, через реку к внутренней части поворота. Внешняя часть петли остается чистой и незащищенной, поэтому эрозия ускоряется, еще больше увеличивая извилистость в мощном петля положительной обратной связи.[63]
Хаос: оболочка брюхоногие моллюски моллюск ткань золотого конуса, Конус текстиль, напоминает Правило 30 клеточный автомат

Поток: вихревая улица облаков на Острова Хуана Фернандеса
Меандры: драматические меандровые шрамы и старицы в широком пойма из Рио-Негро, вид из космоса
Меандры: извилистый путь Rio Cauto, Куба

Меандры: извилистое ползание змеи

Меандры: симметричные мозговой коралл, Diploria strigosa
Волны, дюны
Волны это возмущения, которые несут энергию при движении. Механические волны распространяются через среду - воздух или воду, в результате чего колебаться когда они проходят мимо.[64] Ветровые волны море поверхностные волны которые создают характерный хаотический узор для любого большого водоема, хотя их статистическое поведение можно предсказать с помощью моделей ветровых волн.[65] Когда волны в воде или ветер проходят по песку, они образуют рябь. Когда ветер дует на большие песчаные массы, они создают дюны, иногда на обширных дюнных полях, как в Такламакан пустыня. Дюны могут образовывать ряд узоров, включая полумесяцы, очень длинные прямые линии, звезды, купола, параболы, а также продольные или seif («мечи») формы.[66]
Барханы или серповидные дюны создаются ветром, действующим на песок пустыни; два рога полумесяца и скользкое лицо указать по ветру. Песок обрушивается на поверхность с наветренной стороны, которая находится под углом примерно 15 градусов от горизонтали, и падает на поверхность скольжения, где накапливается до угол естественного откоса песка, который составляет около 35 градусов. Когда поверхность скольжения превышает угол естественного откоса, песок лавины, что является нелинейный поведение: добавление большого количества небольшого количества песка ничего особенного не вызывает, но затем добавление еще небольшого количества песка внезапно вызывает сход большого количества песка.[67] Помимо этой нелинейности, барханы ведут себя скорее как уединенные волны.[68]

Волны: разбивающаяся волна вслед за кораблем

Дюны: песчаные дюны в Такламакан пустыня, из космоса

Дюны: бархан серповидная песчаная дюна
Пузыри, пена
А мыльный пузырь образует сфера, а поверхность с минимальной площадью - наименьшая возможная площадь поверхности для заключенного объема. Два пузыря вместе образуют более сложную форму: внешние поверхности обоих пузырей имеют сферическую форму; к этим поверхностям присоединяется третья сферическая поверхность, поскольку меньший пузырек слегка расширяется в больший.[13]
А мыло это масса пузырей; пены из разных материалов встречаются в природе. Пены, состоящие из мыльные фильмы подчиниться Законы Плато, для которых требуется три мыльных пленки, чтобы встретиться на каждом краю под углом 120 °, и четыре мыльных края, чтобы встретиться в каждой вершине в четырехгранный угол около 109,5 °. Законы Плато также требуют, чтобы пленки были гладкими и непрерывными, а также имели постоянный средняя кривизна в каждой точке. Например, пленка может оставаться в среднем почти плоской, изгибаясь вверх в одном направлении (скажем, слева направо), в то время как изгибаясь вниз в другом направлении (например, спереди назад).[69][70] Конструкции с минимальной площадью можно использовать как палатки. Лорд Кельвин выявил проблему наиболее эффективного способа упаковки ячеек равного объема, как пену в 1887 году; его решение использует только одно твердое тело, усеченные кубические соты с очень слегка изогнутыми гранями, чтобы соответствовать законам Плато. Лучшего решения не было до 1993 года, когда Дени Вир и Роберт Фелан предложили Структура Вира – Фелана; в Пекинский национальный центр водных видов спорта адаптировали структуру для своей внешней стены в Летние Олимпийские игры 2008 года.[71]
В масштабе жизни клетки, рисунки пены обычны; радиолярии, губка спикулы, силикофлагеллят экзоскелеты и кальцитовый скелет морской еж, Cidaris rugosa, все напоминают минеральные слепки границ пены Плато.[72][73] Скелет Радиолярий, Аулония шестиугольная, красивая морская форма, нарисованная Эрнст Геккель, выглядит так, как будто это сфера, полностью состоящая из шестиугольников, но это математически невозможно. В Эйлерова характеристика заявляет, что для любого выпуклый многогранник, количество граней плюс количество вершин (углов) равно количеству ребер плюс два. Результатом этой формулы является то, что любой замкнутый многогранник шестиугольников должен включать ровно 12 пятиугольников, например футбольный мяч, Бакминстер Фуллер геодезический купол, или же фуллерен молекула. Это можно визуализировать, отметив, что сетка из шестиугольников плоская, как лист проволочной сетки, но каждый добавленный пятиугольник заставляет сетку изгибаться (углов меньше, поэтому сетка втягивается).[74]

Мыло из мыльные пузыри: четыре ребра пересекаются в каждой вершине под углами, близкими к 109,5 °, как в двух связях C-H в метан.
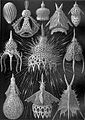
Радиолярии нарисованный Геккель в его Kunstformen der Natur (1904).

Геккеля Спумеллария; скелеты этих радиолярий имеют пеноподобную форму.
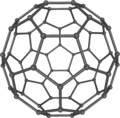
Бакминстерфуллерен C60: Ричард Смолли и коллеги синтезировали фуллерен молекула в 1985 году.

Брохосомы (секреторный микрочастицы произведено цикадки ) часто приблизительно фуллерен геометрия.

Цирковой шатер примерно минимальная поверхность.

Пекинский национальный центр водных видов спорта для Олимпийских игр 2008 года имеет Структура Вира – Фелана.

Равные сферы (пузырьки газа) в поверхностной пене
Мозаики
Мозаики шаблоны, образованные повторением плитка по всей плоской поверхности. Всего 17 группы обоев плиток.[75] Хотя это часто бывает в искусстве и дизайне, точно повторяющиеся плитки труднее найти в живых существах. Ячейки в бумажных гнездах социальных осы, а восковые ячейки в соты построенные медоносными пчелами - хорошо известные примеры. Среди животных костлявые рыбы, рептилии или ящер, или фрукты, подобные Салак защищены перекрывающимися чешуйками или остеодермы, они образуют более или менее точно повторяющиеся единицы, хотя часто масштабы на самом деле постоянно меняются по размеру. Среди цветов змеиная голова рябчатая, Fritillaria meleagris, имеют на лепестках мозаичный узор в виде шахматной доски. Структуры минералы предоставить хорошие примеры регулярно повторяющихся трехмерных массивов. Несмотря на сотни тысяч известных минералов, существует довольно мало возможных типов расположения атомов в кристалл, определяется Кристальная структура, кристаллическая система, и точечная группа; например, ровно 14 Решетки Браве для семи решетчатых систем в трехмерном пространстве.[76]

Кристаллы: кристаллы кубической формы галит (каменная соль); кубическая кристаллическая система, изометрическая гексоктаэдрическая симметрия кристалла

Висмут хоппер кристалл иллюстрирование ступеньки кристальная привычка.
Плитки: мозаичный цветок из рябины на голове змеи, Fritillaria meleagris
Плитки: перекрывающиеся чешуйки обыкновенной плотвы, Рутилус рутилус

Плитки: перекрывающиеся чешуйки змеиного плода или Салак, Salacca zalacca

Мозаичный тротуар: редкое горное образование на Полуостров Тасман
Трещины
Трещины являются линейными отверстиями, которые образуются в материалах для разгрузки стресс. Когда эластичный материал растягивается или сжимается равномерно, в конечном итоге он достигает своей прочности на разрыв, а затем внезапно выходит из строя во всех направлениях, создавая трещины с соединением под углом 120 градусов, поэтому три трещины встречаются в узле. И наоборот, когда неэластичный материал выходит из строя, образуются прямые трещины для снятия напряжения. Дальнейшее напряжение в том же направлении просто открыло бы существующие трещины; напряжение под прямым углом может привести к появлению новых трещин, под углом 90 градусов к старым. Таким образом, рисунок трещин показывает, эластичен материал или нет.[77] В жестком волокнистом материале, таком как кора дуба, образуются трещины, чтобы снять напряжение, как обычно, но они не растут долго, поскольку их рост прерывается пучками прочных эластичных волокон. Поскольку каждый вид дерева имеет свою собственную структуру на уровне клеток и молекул, у каждого есть свой собственный образец расщепления коры.[78]

Поверхность старой керамики, белая глазурь с трещинами в основном под углом 90 °

Сушка неупругой грязи в Ранн из Катча с трещинами в основном под углом 90 °

Прожилками габбро с трещинами 90 °, около Сгурр на Стри, Скай

Сушка эластичной грязи в Сицилия в основном с трещинами под углом 120 °

Охлажденный базальт в Дорога гигантов. Вертикальные трещины, в основном 120 °, образующие шестиугольные колонны

Ствол пальмы с ветвящимися вертикальными трещинами (и горизонтальными рубцами на листьях)
Пятна, полосы
Замечены леопарды и божьи коровки; скалярии и зебры полосатые.[79] Эти шаблоны имеют эволюционный объяснение: у них есть функции которые увеличивают шансы того, что потомство животного с рисунком выживет и будет воспроизводиться. Одна из функций рисунков животных - камуфляж;[25] например, леопард что труднее увидеть ловит больше добычи. Другая функция сигнализация[26] - например, божья коровка с меньшей вероятностью подвергнется нападению хищный птиц, которые охотятся с виду, если они имеют жирные предупреждающие цвета, а также неприятно горький или ядовитый, или же имитирует другие неприятные насекомые. Молодая птица может увидеть насекомое с предупреждающим узором, такое как божья коровка, и попытаться съесть его, но сделает это только один раз; очень скоро оно выплюнет горькое насекомое; остальные божьи коровки останутся нетронутыми. Молодые леопарды и божьи коровки, унаследовавшие гены которые каким-то образом создают пятнистость, выживают. Но хотя эти эволюционные и функциональные аргументы объясняют, почему этим животным нужны их паттерны, они не объясняют, как эти паттерны формируются.[79]

Дирс красавица бабочка, Колобура дирче

Зебра Греви, Equus Grevyi

Королевский ангел, Pygoplites diacanthus

Леопард, Panthera pardus pardus

Массив божьи коровки к Г.Г. Якобсон

Схема размножения каракатица, Сепия лекарственная
Формирование паттерна
Алан Тьюринг,[16] а позже математический биолог Джеймс Мюррей,[80] описал механизм, который самопроизвольно создает пятнистые или полосатые узоры: система реакция – диффузия.[81] В клетках молодого организма есть гены, которые могут быть включены химическим сигналом, морфоген, что приводит к росту структуры определенного типа, скажем, темного пигментированного участка кожи. Если морфоген присутствует повсюду, получается ровная пигментация, как у черного леопарда. Но если он распределен неравномерно, могут образоваться пятна или полосы. Тьюринг предположил, что может быть Обратная связь контроль продукции самого морфогена. Это может вызвать постоянные колебания количества морфогена, распространяющегося по телу. Второй механизм необходим для создания стоячая волна паттерны (приводящие к пятнам или полосам): химический ингибитор, который выключает выработку морфогена и который сам диффундирует по телу быстрее, чем морфоген, что приводит к схеме активатор-ингибитор. В Реакция Белоусова – Жаботинского небиологический пример такой схемы, химический осциллятор.[81]
Более поздние исследования позволили создать убедительные модели узоров, столь же разнообразных, как полосы зебры, пятна жирафа, пятна ягуара (средне-темные пятна, окруженные темными разорванными кольцами) и узоры на панцирях божьих коровок (различные геометрические схемы пятен и полос, см. Иллюстрации).[82] Ричард Прам модели ингибирования активации, разработанные на основе работы Тьюринга, используют шесть переменных для учета наблюдаемого диапазона из девяти основных паттернов пигментации внутри пера, от простейшего центрального пигментного пятна до концентрических пятен, полос, шевронов, глазного пятна и т. д. пара центральных пятен, ряды парных пятен и ряд точек.[83][84]:6 Более сложные модели имитируют сложный узор перьев цесарок. Нумида Мелеагрис в котором отдельные перья имеют переходы от полос у основания к массиву точек на дальнем (дистальном) конце. Для этого требуется колебание, создаваемое двумя запрещающими сигналами, взаимодействующими как в пространстве, так и во времени.[84]:7–8
Шаблоны могут формироваться по другим причинам в растительный ландшафт из куст тигра[85] и еловые волны.[86] Полосы тигрового куста встречаются на засушливых склонах, где рост растений ограничен дождями. Каждая примерно горизонтальная полоса растительности эффективно собирает дождевую воду из голой зоны непосредственно над ней.[85] Пихтовые волны возникают в лесах на горных склонах после ветрового волнения, в период возобновления. Когда деревья падают, деревья, которые они укрывали, становятся незащищенными и, в свою очередь, с большей вероятностью будут повреждены, поэтому промежутки имеют тенденцию расширяться по ветру. Между тем с наветренной стороны растут молодые деревья, защищенные ветровой тенью оставшихся высоких деревьев.[86] Природные узоры иногда образуют животные, как в Мима курганы Северо-Запада Соединенных Штатов и некоторых других территорий, которые, по-видимому, были созданы за многие годы в результате роющей деятельности карманные суслики,[87] а так называемые круги фей Намибии, по всей видимости, возникли в результате взаимодействия конкурирующих групп песчаных термитов и конкуренции за воду среди пустынных растений.[88]
В многолетнемерзлых грунтах с активным верхним слоем, подверженным ежегодному промерзанию и оттаиванию, узорчатая земля может образовывать, создавая круги, сети, ледяной клин многоугольники, ступеньки и полосы. Термическое сжатие вызывает образование усадочных трещин; во время оттепели вода заполняет трещины, расширяясь, образуя лед при следующем замерзании, и превращая трещины в клинья. Эти трещины могут соединяться, образуя многоугольники и другие формы.[89]
В трещинный узор который развивается в головном мозге позвоночных, вызывается физическим процессом ограниченного расширения, зависящим от двух геометрических параметров: относительного тангенциального расширения коры и относительной толщины кора. Подобные модели извилины (пики) и борозды (впадины) были продемонстрированы на моделях мозга, начиная с гладких, слоистых гелей, с узорами, вызванными сжимающими механическими силами, возникающими в результате расширения внешнего слоя (представляющего кору) после добавления растворителя. Численные модели в компьютерном моделировании подтверждают естественные и экспериментальные наблюдения, что структура складок поверхности увеличивается в больших размерах мозга.[90][91]
Гигантская рыба-фугу, Тетраодон мбу

Деталь рисунка кожи гигантского фугу

Снимок моделирования Реакция Белоусова – Жаботинского

Цесарка в шлеме, Нумида Мелеагрис, перья переходят от решетчатых к пятнистым, как в перьях, так и поперек птицы

Вид с воздуха на куст тигра плато в Нигер

Узорчатая земля: таяние пинго с окружающими ледяной клин полигоны рядом Туктояктук, Канада
Смотрите также
Рекомендации
Сноски
- ^ Так называемой Пифагорейцы, которые первыми занялись математикой, не только продвинули этот предмет, но и пресытились им, они вообразили, что принципы математики являются принципами всех вещей. Аристотель, Метафизика 1–5 , c. 350 г. до н.э.
- ^ Аристотель сообщает об Эмпедокле, утверждая, что «[где] тогда все обернулось так, как если бы это происходило с определенной целью, там существа выжили, будучи случайно смешанными подходящим образом; но там, где этого не произошло, существа погибли ". Физика, B8, 198b29 в Kirk, et al., 304).
Цитаты
- ^ Стивенс 1974, п. 3.
- ^ Балагер, Марк (7 апреля 2009 г.) [2004]. «Платонизм в метафизике». Стэнфордская энциклопедия философии. Получено 4 мая 2012.
- ^ а б c d е Ливио, Марио (2003) [2002]. Золотое сечение: история Фи, самого удивительного числа в мире (Первая торговая книга в мягкой обложке, ред.). Нью-Йорк: Бродвей Книги. п. 110. ISBN 978-0-7679-0816-0.
- ^ Да Винчи, Леонардо (1971). Тейлор, Памела (ред.). Записные книжки Леонардо да Винчи. Новая американская библиотека. п. 121.
- ^ Падован, Ричард (1999). Пропорции: наука, философия, архитектура. Тейлор и Фрэнсис. С. 305–306. ISBN 978-0-419-22780-9.
- ^ Падован, Ричард (2002). «Пропорции: наука, философия, архитектура». Сетевой журнал Nexus. 4 (1): 113–122. Дои:10.1007 / s00004-001-0008-7.
- ^ Цейзинг, Адольф (1854). Neue Lehre van den Proportionen des meschlischen Körpers. предисловие.
- ^ а б Ливио, Марио (2003) [2002]. Золотое сечение: история Фи, самого удивительного числа в мире (Первая торговая книга в мягкой обложке, ред.). Нью-Йорк: Бродвей Книги. п. 111. ISBN 978-0-7679-0816-0.
- ^ О Д'Арси. Д'Арси 150. Университет Данди и Сент-Эндрюсский университет. Проверено 16 октября 2012 года.
- ^ Сингх, Пармананд. Ачарья Хемачандра и (так называемые) числа Фибоначчи. Математика. Эд. Сиван, 20 (1): 28–30, 1986. ISSN 0047-6269
- ^ Нотт, Рон. «Кролики Фибоначчи». Университет Суррея Факультет инженерии и физических наук.
- ^ Браун, Томас (1658). Как природа геометризирует. Сад Кира.
- ^ а б Стюарт 2001 С. 108–109.
- ^ Бал 2009, п. 41.
- ^ Ханнави, Джон (2007). Энциклопедия фотографии девятнадцатого века. 1. CRC Press. п. 149. ISBN 978-0-415-97235-2.
- ^ а б Тьюринг, А. (1952). «Химические основы морфогенеза». Философские труды Королевского общества B. 237 (641): 37–72. Bibcode:1952РСПТБ.237 ... 37Т. Дои:10.1098 / рстб.1952.0012.
- ^ Бал 2009 С. 163, 247–250.
- ^ а б c Розенберг, Гжегож; Саломаа, Арто. Математическая теория L-систем. Академическая пресса, Нью-Йорк, 1980. ISBN 0-12-597140-0
- ^ а б Мандельброт, Бенуа Б. (1983). Фрактальная геометрия природы. Макмиллан.
- ^ Форбс, Питер. Вся эта бесполезная красота. Хранитель. Обзор: Научная литература. 11 февраля 2012 г.
- ^ Стивенс 1974, п. 222.
- ^ Стин, Л.А. (1988). «Наука узоров». Наука. 240 (4852): 611–616. Bibcode:1988Научный ... 240..611S. Дои:10.1126 / science.240.4852.611. PMID 17840903. S2CID 4849363.
- ^ Девлин, Кит. Математика: наука о закономерностях: поиск порядка в жизни, разуме и Вселенной (Библиотека в мягкой обложке Scientific American) 1996
- ^ Татаркевич, Владислав. Совершенство в науках. II. Совершенство в физике и химии, Диалектика и гуманизм, т. VII, вып. 2 (весна 1980 г.), стр. 139.
- ^ а б c Дарвин, Чарльз. О происхождении видов. 1859 г., глава 4.
- ^ а б Виклер, Вольфганг (1968). Мимикрия у растений и животных. Нью-Йорк: Макгроу-Хилл.
- ^ Poulin, R .; Grutter, A.S. (1996) "Симбиоз очистки: приблизительное и адаптивное объяснения ". Бионаука 46(7): 512–517. (требуется подписка)
- ^ Конинг, Росс (1994). "Информационный веб-сайт физиологии растений". Адаптации к опылению. Получено 2 мая, 2012.
- ^ Стюарт 2001 С. 48–49.
- ^ Стюарт 2001 С. 64–65.
- ^ Стюарт 2001, п. 52.
- ^ Стюарт 2001 С. 82–84.
- ^ Стюарт 2001, п. 60.
- ^ Стюарт 2001, п. 71.
- ^ Hickman, Cleveland P .; Робертс, Ларри С .; Ларсон, Аллан (2002). «Разнообразие животных» (PDF). Глава 8: Двусторонние животные акцеломаты (Третье изд.). п. 139. Архивировано с оригинал (PDF) 17 мая 2016 г.. Получено 25 октября, 2012.
- ^ Sumrall, Colin D .; Рэй, Грегори А. (январь 2007 г.). «Онтогенез в летописи окаменелостей: разнообразие строений тела и эволюция« аберрантной »симметрии у палеозойских иглокожих». Палеобиология. 33 (1): 149–163. Дои:10.1666/06053.1. JSTOR 4500143. S2CID 84195721.
- ^ Рихтер, Жан Поль, изд. (1970) [1880]. Записные книжки Леонардо да Винчи. Дувр. ISBN 0-486-22572-0. Получено 2007-02-04.
- ^ а б Палка, Джо (26 декабря 2011 г.). "Мудрость деревьев (Леонардо да Винчи знал это)". Утренний выпуск. энергетический ядерный реактор. Получено 2019-07-16.
- ^ Минамино, Рёко; Татено, Масаки (2014). «Ветвление деревьев: правило Леонардо да Винчи против биомеханических моделей». PLoS One. Vol. 9 нет. 4. п. e93535. Дои:10.1371 / journal.pone.0093535.
- ^ Сокольничий, Кеннет (2003). Фрактальная геометрия: математические основы и приложения. Джон Вили.
- ^ Бриггс, Джон (1992). Фракталы: модели хаоса. Темза и Гудзон. п. 148.
- ^ Бэтти, Майкл (1985-04-04). «Фракталы - геометрия между измерениями». Новый ученый. 105 (1450): 31.
- ^ Мейер, Ив; Рокес, Сильви (1993). Прогресс в вейвлет-анализе и приложениях: материалы Международной конференции "Вейвлеты и приложения", Тулуза, Франция - июнь 1992 г.. Atlantica Séguier Frontières. п. 25. ISBN 9782863321300.
- ^ Карбоне, Алессандра; Громов, Михаил; Прусинкевич, Пшемыслав (2000). Формирование паттернов в биологии, видении и динамике. World Scientific. п. 78. ISBN 9789810237929.
- ^ Hahn, Horst K .; Георг, Манфред; Пайтген, Хайнц-Отто (2005). «Фрактальные аспекты трехмерной конструктивной оптимизации сосудов». In Losa, Gabriele A .; Нонненмахер, Тео Ф. (ред.). Фракталы в биологии и медицине. Springer. С. 55–66.
- ^ Садех, Саназ (2017). «Плазменная мембрана разделена самоподобной кортикальной актиновой сеткой». Физический обзор X. 7 (1): 011031. arXiv:1702.03997. Bibcode:2017PhRvX ... 7a1031S. Дои:10.1103 / PhysRevX.7.011031. ЧВК 5500227. PMID 28690919.
- ^ Аддисон, Пол С. (1997). Фракталы и хаос: иллюстрированный курс. CRC Press. С. 44–46.
- ^ Маор, Эли. д: История числа. Princeton University Press, 2009. Страница 135.
- ^ Бал 2009 С. 29–32.
- ^ "Спиральные решетки и парастичи". Смит-колледж. Архивировано из оригинал 26 мая 2010 г.. Получено 24 сентября 2013.
- ^ а б Каппрафф, Джей (2004). «Рост растений: исследование в цифрах» (PDF). Forma. 19: 335–354.
- ^ Бал 2009, п. 13.
- ^ Кокстер, Х. С. М. (1961). Введение в геометрию. Вайли. п. 169.
- ^ Прусинкевич, Пшемыслав; Линденмайер, Аристид (1990). Алгоритмическая красота растений. Springer-Verlag. стр.101–107. ISBN 978-0-387-97297-8.
- ^ Левитов Л.С. (15 марта 1991 г.). «Энергетический подход к филлотаксису» (PDF). Europhys. Латыш. 14 (6): 533–9. Bibcode:1991ЭЛ ..... 14..533Л. Дои:10.1209/0295-5075/14/6/006.(требуется подписка)
- ^ Дуади, S; Кудер, Ю. (март 1992 г.). «Филлотаксис как физический процесс самоорганизованного роста». Письма с физическими проверками. 68 (13): 2098–2101. Bibcode:1992ПхРвЛ..68.2098Д. Дои:10.1103 / PhysRevLett.68.2098. PMID 10045303.(требуется подписка)
- ^ Бал 2009 С. 163, 249–250.
- ^ Лоренц, Эдвард Н. (Март 1963 г.). «Детерминированный непериодический поток». Журнал атмосферных наук. 20 (2): 130–141. Bibcode:1963JAtS ... 20..130L. Дои:10.1175 / 1520-0469 (1963) 020 <0130: DNF> 2.0.CO; 2.
- ^ Элайди, Сабер Н. (1999). Дискретный хаос. Чепмен и Холл / CRC. п. 117.
- ^ Руэлль, Дэвид. Шанс и хаос. Издательство Принстонского университета, 1991.
- ^ Вольфрам, Стивен. Новый вид науки. Вольфрам Медиа, 2002.
- ^ фон Карман, Теодор. Аэродинамика. Макгроу-Хилл (1963): ISBN 978-0070676022. Довер (1994): ISBN 978-0486434858.
- ^ Леваль, Жак (2006). «Разделение потоков и вторичный поток: Раздел 9.1» (PDF). Конспект лекций по динамике несжимаемой жидкости: феноменология, концепции и аналитические инструменты. Сиракузы, штат Нью-Йорк: Сиракузский университет. Архивировано из оригинал (PDF) 29 сентября 2011 г..
- ^ Френч, А. Колебания и волны. Нельсон Торнс, 1971.
- ^ Толман, Х.Л. (2008), "Практическое моделирование ветрового волнения", в Махмуд, М.Ф. (ред.), CBMS Conference Proceedings on Water Waves: Theory and Experiment (PDF), Университет Говарда, США, 13–18 мая 2008 г .: World Scientific Publ.CS1 maint: location (связь)
- ^ «Типы дюн». USGS. 29 октября 1997 г.. Получено 2 мая, 2012.
- ^ Strahler, A. & Archibold, O.W. Физическая география: наука и системы окружающей человека среды. Джон Вили, 4-е издание, 2008 г. Страница 442.
- ^ Schwämmle, V .; Херрман, Х.Дж. (2003). «Уединенно-волновое поведение песчаных дюн». Природа. 426 (11 декабря): 619–620 Абстрактный. Bibcode:2003Натура.426..619S. Дои:10.1038 / 426619a. PMID 14668849. S2CID 688445.(требуется подписка)
- ^ Бал 2009, п. 68.
- ^ Фредерик Дж. Альмгрен-младший. и Джин Э. Тейлор, Геометрия мыльных пленок и мыльных пузырей, Scientific American, т. 235, стр. 82–93, июль 1976 г.
- ^ Бал 2009 С. 73–76.
- ^ Бал 2009 С. 96–101.
- ^ Броди, Кристина (февраль 2005 г.). "Геометрия и закономерности в природе 3: дыры в тестах радиолярий и диатомовых водорослей". Микроскопия-Великобритания. Получено 28 мая, 2012.
- ^ Бал 2009 С. 51–54.
- ^ Армстронг, М.А. (1988). Группы и симметрия. Нью-Йорк: Springer-Verlag.
- ^ Крюк, J.R .; Холл, Е. Физика твердого тела (2-е издание). Манчестерская серия по физике, John Wiley & Sons, 2010. ISBN 978-0-471-92804-1
- ^ Стивенс 1974, п. 207.
- ^ Стивенс 1974, п. 208.
- ^ а б Бал 2009 С. 156–158.
- ^ Мюррей, Джеймс Д. (9 марта 2013 г.). Математическая биология. Springer Science & Business Media. С. 436–450. ISBN 978-3-662-08539-4.
- ^ а б Бал 2009 С. 159–167.
- ^ Бал 2009 С. 168–180.
- ^ Ротенберг 2011 С. 93–95.
- ^ а б Prum, Ричард О.; Уильямсон, Скотт (2002). «Реакционно-диффузионные модели формирования пигментного рисунка внутри пера» (PDF). Труды Лондонского королевского общества B. 269 (1493): 781–792. Дои:10.1098 / rspb.2001.1896. ЧВК 1690965. PMID 11958709.
- ^ а б Тонгуэй, Д.Дж .; Валентин, С. и Сегиери, Дж. (2001). Полосатая растительность в засушливых и полузасушливых средах. Нью-Йорк: Springer-Verlag.
- ^ а б Д'Аванцо, К. (22 февраля 2004 г.). "Еловые волны: восстановление хвойных лесов Новой Англии". TIEE. Получено 26 мая 2012.
- ^ Морелль, Ребекка (09.12.2013). "'Цифровые суслики раскрывают тайну кургана Мима ". Новости BBC. Получено 9 декабря 2013.
- ^ Пример, Ян (2017-01-18). «Секрет« волшебных кругов »Намибии наконец-то может быть объяснен». Хранитель. Получено 18 января 2017.
- ^ «Вечная мерзлота: узорчатая земля». Инженерный корпус армии США. Архивировано из оригинал 7 марта 2015 г.. Получено 17 февраля 2015.
- ^ Гхош, Тиа. "Необычный узор складывания человеческого мозга, воссозданный в чане". Scientific American. Получено 5 апреля 2018.
- ^ Таллинен, Туома; Чанг, Джун Ён; Биггинс, Джон С .; Махадеван, Л. (2014). «Гирификация от ограниченного коркового расширения». Труды Национальной академии наук Соединенных Штатов Америки. 111 (35): 12667–12672. arXiv:1503.03853. Bibcode:2014ПНАС..11112667Т. Дои:10.1073 / pnas.1406015111. ЧВК 4156754. PMID 25136099.
Библиография
Авторы-новаторы
- Фибоначчи, Леонардо. Liber Abaci, 1202.
- ———— перевод Сиглера, Лоуренс Э. Liber Abaci Фибоначчи. Спрингер, 2002.
- Геккель, Эрнст. Kunstformen der Natur (Формы искусства в природе), 1899–1904.
- Томпсон, Д'Арси Вентворт. О росте и форме. Кембридж, 1917 год.
Общие книги
- Адам, Джон А. Математика в природе: моделирование закономерностей в мире природы. Princeton University Press, 2006.
- Болл, Филипп (2009). Узоры природы: гобелен из трех частей. 1: Фигуры. Издательство Оксфордского университета.CS1 maint: ref = harv (связь)
- Болл, Филипп (2009). Узоры природы: гобелен из трех частей. 2: Поток. Издательство Оксфордского университета.
- Болл, Филипп (2009). Узоры природы: гобелен из трех частей. 3. Филиалы. Издательство Оксфордского университета.
- Болл, Филипп. Узоры в природе. Чикаго, 2016.
- Мерфи, Пэт и Нил, Уильям. По замыслу природы. Книги Хроники, 1993.
- Ротенберг, Дэвид (2011). Выживание прекрасного: искусство, наука и эволюция. Bloomsbury Press.CS1 maint: ref = harv (связь)
- Стивенс, Питер С. (1974). Узоры в природе. Little, Brown & Co.CS1 maint: ref = harv (связь)
- Стюарт, Ян (2001). Какая форма у снежинки? Волшебные числа в природе. Вайденфельд и Николсон.CS1 maint: ref = harv (связь)
Узоры с натуры (как искусство)
- Эдмайер, Бернар. Узоры Земли. Phaidon Press, 2007.
- Макнаб, Мэгги. Дизайн от природы: использование универсальных форм и принципов в дизайне. Новые райдеры, 2012.
- Накамура, Шигеки. Справочник по образцам: 250 узоров, вдохновленных природой.. Книги 1 и 2. Рокпорт, 2009.
- О'Нил, Полли. Поверхности и текстуры: Визуальный справочник. Черный, 2008.
- Портер, Элиот, и Глейк, Джеймс. Природный хаос. Пингвин викинг, 1990.