Усеченные кубические соты - Bitruncated cubic honeycomb
| Усеченные кубические соты | |
|---|---|
  | |
| Тип | Равномерные соты |
| Символ Шлефли | 2т {4,3,4} т1,2{4,3,4} |
| Диаграмма Кокстера-Дынкина | |
| Тип ячейки | (4.6.6) |
| Типы лица | квадрат {4} шестиугольник {6} |
| Край фигура | равнобедренный треугольник {3} |
| Фигура вершины |  (тетрагональный дисфеноид ) |
| Космическая группа Обозначение фибрифолда Обозначение Кокстера | Я3м (229) 8о:2 [[4,3,4]] |
| Группа Кокстера | , [4,3,4] |
| Двойной | Сплюснутый тетраэдр Дисфеноидные четырехгранные соты Клетка:  |
| Характеристики | изогональный, изотоксальный, изохорный |

В усеченные кубические соты заполняет пространство мозаика (или же соты ) в Евклидово 3-пространство состоит из усеченные октаэдры (или, что то же самое, усеченный битами кубики). Имеет 4 усеченные октаэдры вокруг каждой вершины. Полностью состоящий из усеченные октаэдры, это клеточно-транзитивный. Это также реберно-транзитивный, с двумя шестиугольниками и одним квадратом на каждом краю, и вершинно-транзитивный. Это один из 28 однородные соты.
Джон Хортон Конвей называет эту соту усеченный октаэдр в его Архитектурная и катоптическая мозаика список с двойным, называемым сплюснутый тетраэдрил, также называемый дисфеноидные четырехгранные соты. Хотя регулярный тетраэдр не может мозаизировать пространство в одиночку, этот дуал имеет идентичные дисфеноидный тетраэдр клетки с равнобедренный треугольник лица.
Геометрия
Это может быть реализовано как Мозаика Вороного из объемно-центрированный кубический решетка. Лорд Кельвин предположил, что вариант усеченные кубические соты (с изогнутыми гранями и краями, но той же комбинаторной структурой) - оптимальная пена для мыльных пузырей. Тем не менее Структура Вира – Фелана представляет собой менее симметричную, но более эффективную пену из мыльных пузырей.
Соты представляют собой пермутоэдр тесселяция для 3-х пространств. Координаты вершин одного октаэдра представляют собой гиперплоскость целых чисел в 4-м пространстве, в частности перестановки из (1,2,3,4). Тесселяция формируется из переведенных копий внутри гиперплоскости.
Тесселяция - это самая высокая мозаика из параллелоэдры в 3-м пространстве.
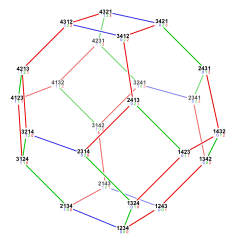
Прогнозы
В усеченные кубические соты может быть ортогонально спроецирован в евклидову плоскость с различным расположением симметрии. Форма высшей (гексагональной) симметрии проектируется в неоднородную ромбитогексагональная черепица. Квадратная проекция симметрии образует две перекрывающиеся усеченная квадратная мозаика, которые объединяются как квадратная черепица с фаской.
| Симметрия | p6m (* 632) | p4m (* 442) | pmm (* 2222) | ||
|---|---|---|---|---|---|
| Твердый |  |  |  |  |  |
| Рамка |  |  |  |  |  |
Симметрия
Фигура вершины этой соты - это дисфеноидный тетраэдр, а также Тетраэдр Гурса (фундаментальная область ) для Группа Кокстера. Эта сотовая структура имеет четыре одинаковых конструкции, при этом усеченные октаэдрические ячейки имеют разные Группы Кокстера и Конструкции Wythoff. Эти однородные симметрии можно представить, раскрасив по-разному ячейки в каждой конструкции.
| Космическая группа | Я3м (229) | Вечера3м (221) | FM3м (225) | F43 мес. (216) | Fd3м (227) |
|---|---|---|---|---|---|
| Фибрифолд | 8о:2 | 4−:2 | 2−:2 | 1о:2 | 2+:2 |
| Группа Кокстера | ×2 [[4,3,4]] =[4[3[4]]] | [4,3,4] =[2[3[4]]] | [4,31,1] =<[3[4]]> | [3[4]] | ×2 [[3[4]]] =[[3[4]]] |
| Диаграмма Кокстера | |||||
| усеченные октаэдры | 1 | 1:1 | 2:1:1 | 1:1:1:1 | 1:1 |
| Фигура вершины |  |  |  |  |  |
| Вершина фигура симметрия | [2+,4] (заказ 8) | [2] (заказ 4) | [ ] (заказ 2) | [ ]+ (заказ 1) | [2]+ (заказ 2) |
| Изображение Раскрашено клетка |  |  |  |  |  |
Связанные многогранники и соты

[4,3,4], ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Группа Кокстера генерирует 15 перестановок однородных мозаик, 9 с различной геометрией, включая чередующиеся кубические соты. В расширенный кубические соты (также известные как тессерактические соты) геометрически идентичны кубическим сотам.
, Группа Кокстера генерирует 15 перестановок однородных мозаик, 9 с различной геометрией, включая чередующиеся кубические соты. В расширенный кубические соты (также известные как тессерактические соты) геометрически идентичны кубическим сотам.
| C3 соты | |||||
|---|---|---|---|---|---|
| Космос группа | Фибрифолд | Расширенный симметрия | Расширенный диаграмма | Заказ | Соты |
| Вечера3м (221) | 4−:2 | [4,3,4] | ×1 | ||
| FM3м (225) | 2−:2 | [1+,4,3,4] ↔ [4,31,1] | ↔ | Половина | |
| я43м (217) | 4о:2 | [[(4,3,4,2+)]] | Половина × 2 | ||
| Fd3м (227) | 2+:2 | [[1+,4,3,4,1+]] ↔ [[3[4]]] | ↔ | Квартал × 2 | |
| Я3м (229) | 8о:2 | [[4,3,4]] | ×2 | ||
[4,31,1], ![]()
![]()
![]()
![]()
![]() , Группа Кокстера генерирует 9 перестановок однородных мозаик, 4 с различной геометрией, включая чередующиеся кубические соты.
, Группа Кокстера генерирует 9 перестановок однородных мозаик, 4 с различной геометрией, включая чередующиеся кубические соты.
| B3 соты | |||||
|---|---|---|---|---|---|
| Космос группа | Фибрифолд | Расширенный симметрия | Расширенный диаграмма | Заказ | Соты |
| FM3м (225) | 2−:2 | [4,31,1] ↔ [4,3,4,1+] | ↔ | ×1 | |
| FM3м (225) | 2−:2 | <[1+,4,31,1]> ↔ <[3[4]]> | ↔ | ×2 | |
| Вечера3м (221) | 4−:2 | <[4,31,1]> | ×2 | ||
Эти соты - одна из пять отдельных однородных сот[1] построенный Группа Кокстера. Симметрию можно умножить на симметрию колец в Диаграммы Кокстера – Дынкина:
| Соты формата А3 | ||||||
|---|---|---|---|---|---|---|
| Космос группа | Фибрифолд | Квадрат симметрия | Расширенный симметрия | Расширенный диаграмма | Расширенный группа | Сотовые диаграммы |
| F43м (216) | 1о:2 | а1 | [3[4]] | (Никто) | ||
| FM3м (225) | 2−:2 | d2 | <[3[4]]> ↔ [4,31,1] | ↔ | ×21 ↔ | |
| Fd3м (227) | 2+:2 | g2 | [[3[4]]] или [2+[3[4]]] | ↔ | ×22 | |
| Вечера3м (221) | 4−:2 | d4 | <2[3[4]]> ↔ [4,3,4] | ↔ | ×41 ↔ | |
| я3 (204) | 8−o | r8 | [4[3[4]]]+ ↔ [[4,3+,4]] | ↔ | ½×8 ↔ ½×2 | |
| Я3м (229) | 8о:2 | [4[3[4]]] ↔ [[4,3,4]] | ×8 ↔ ×2 | |||
Альтернативная форма
| Чередующиеся битоусеченные кубические соты | |
|---|---|
| Тип | Выпуклые соты |
| Символ Шлефли | 2 с {4,3,4} 2с {4,31,1} sr {3[4]} |
| Диаграммы Кокстера | |
| Клетки | тетраэдр икосаэдр |
| Фигура вершины |  |
| Группа Кокстера | [[4,3+,4]], |
| Двойной | Соты из десяти бриллиантов Клетка:  |
| Характеристики | вершинно-транзитивный |
Эти соты можно чередовались, создавая пиритоэдр икосаэдры из усеченных октаэдров с созданными в промежутках диспеноидными тетраэдрическими ячейками. Есть три конструкции из трех связанных Диаграммы Кокстера-Дынкина: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() , и
, и ![]()
![]()
![]()
![]()
![]() . Они обладают симметрией [4,3+,4], [4,(31,1)+] и [3[4]]+ соответственно. Первую и последнюю симметрию можно удвоить как [[4,3+, 4]] и [[3[4]]]+.
. Они обладают симметрией [4,3+,4], [4,(31,1)+] и [3[4]]+ соответственно. Первую и последнюю симметрию можно удвоить как [[4,3+, 4]] и [[3[4]]]+.
Двойные соты состоят из ячеек, называемых декаэдры из десяти бубен.
| Космическая группа | я3 (204) | Вечера3 (200) | FM3 (202) | Fd3 (203) | F23 (196) |
|---|---|---|---|---|---|
| Фибрифолд | 8−o | 4− | 2− | 2о + | 1о |
| Группа Кокстера | [[4,3+,4]] | [4,3+,4] | [4,(31,1)+] | [[3[4]]]+ | [3[4]]+ |
| Диаграмма Кокстера | |||||
| Заказ | двойной | полный | половина | четверть двойной | четверть |
| Изображение раскрашенный клетками |  |  |  |  |  |
Эти соты представлены атомами бора α-ромбиэдрический кристалл. Центры икосаэдров расположены в ГЦК-позициях решетки.[2]
Связанные многогранники
Неоднородные варианты с симметрией [4,3,4] и двумя типами усеченных октаэдров могут быть удвоены путем размещения двух типов усеченных октаэдров для получения неоднородных сот с усеченные октаэдры и шестиугольные призмы (как дитригональные трапеции). Его вершина - фигура C2v-симметричный треугольная бипирамида.
Затем эти соты можно чередовать, чтобы получить другие неоднородные соты с пиритоэдрические икосаэдры, октаэдры (как треугольные антипризмы), и тетраэдры (как сфеноиды). Его вершинная фигура имеет C2v симметрия и состоит из 2 пятиугольники, 4 прямоугольники, 4 равнобедренные треугольники (разделены на два набора по 2) и 4 разносторонние треугольники.
Смотрите также
Примечания
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 21, Именование архимедовых и каталонских многогранников и плиток, Архитектурные и катоптрические мозаики, стр. 292-298, включает все непризматические формы)
- Георгий Ольшевский, Однородные паноплоидные тетракомбы, Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
- Бранко Грюнбаум, Равномерные мозаики трехмерного пространства. Геомбинаторика 4(1994), 49 - 56.
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Однородные заполнители пространств)
- А. Андреини, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (О правильных и полуправильных сетях многогранников и соответствующих коррелятивных сетях), Mem. Итальянское общество науки, сер. 3, 14 (1905) 75–129.
- Клитцинг, Ричард. "3D евклидовы соты o4x3x4o - партия - O16".
- Однородные соты в 3-х пространствах: партия 05
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X.