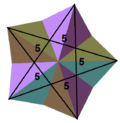
Большой додекаэдр - Great dodecahedron

Большой додекаэдр
Тип	Многогранник Кеплера – Пуансо
Звездчатость основной	правильный додекаэдр
Элементы	F = 12, E = 30 V = 12 (χ = -6)
Лица по сторонам	12{5}
Символ Шлефли	{5,​^5⁄2}
Конфигурация лица	V (^5⁄2)^5
Символ Wythoff	​^5⁄2 | 2 5
Диаграмма Кокстера
Группа симметрии	ячас, H3, [5,3], (*532)
Рекомендации	U35, C44, W21
Характеристики	Обычный невыпуклый
(5^5)/2 (Фигура вершины )	Малый звездчатый додекаэдр (двойственный многогранник )

3D модель большого додекаэдра

В геометрия, то большой додекаэдр это Многогранник Кеплера – Пуансо, с Символ Шлефли {5,5 / 2} и Диаграмма Кокстера – Дынкина из . Это один из четырех невыпуклый правильные многогранники. Он состоит из 12 пятиугольник грани (шесть пар параллельных пятиугольников), с пятью пятиугольниками, встречающимися в каждой вершине, пересекающимися друг с другом, образуя пентаграмматический дорожка.

Открытие большого додекаэдра иногда приписывают Луи Пуансо в 1810 году, хотя в книге 1568 года есть рисунок чего-то очень похожего на большой додекаэдр. Perspectiva Corporum Regularium к Венцель Ямнитцер.

Большой додекаэдр может быть построен аналогично пентаграмме, ее двумерному аналогу, посредством расширения (п-1) -D пятиугольный многогранник грани ядра пМногогранник D (пятиугольники для большого додекаэдра и отрезки прямых для пентаграммы), пока фигура снова не закроется.

Изображений

Прозрачная модель	Сферическая черепица
(С анимацией )	Этот многогранник представляет собой сферическая черепица с плотностью 3. (Одна сферическая грань пятиугольника показана выше желтым цветом)
Сеть	Звездчатость
× 20 Сетка для геометрии поверхности; двадцать равнобедренных треугольных пирамид, расположенных как грани икосаэдр	Его также можно построить как второй из трех звёздчатые додекаэдра и обозначается как Модель Веннингера [W21].

Связанные многогранники

Анимированная последовательность усечения от {5/2, 5} до {5, 5/2}

Он разделяет то же самое расположение кромок как выпуклый регулярный икосаэдр; соединение с обоими является малый сложный икосододекаэдр.

Если рассматривать только видимую поверхность, она имеет ту же топологию, что и триакис икосаэдр пирамиды вогнутые, а не выпуклые. В раскопанный додекаэдр можно рассматривать как тот же процесс, применяемый к правильному додекаэдру, хотя этот результат не является регулярным.

А усечение процесс, примененный к большому додекаэдру, дает ряд невыпуклые равномерные многогранники. Усечение краев до точек дает додекадодекаэдр как выпрямленный большой додекаэдр. Процесс завершается биректификацией, уменьшая исходные грани до точек и создавая малый звездчатый додекаэдр.

Звёздчатые формы додекаэдра
Платоново твердое тело	Тела Кеплера – Пуансо
Додекаэдр	Малый звездчатый додекаэдр	Большой додекаэдр	Большой звездчатый додекаэдр

Имя	Малый звездчатый додекаэдр	Додекадодекаэдр	Усеченный здорово додекаэдр	Большой додекаэдр
Кокстер-Дынкин диаграмма
Рисунок

использование

• Эта форма послужила основой для Кубик Рубика -подобно Александра Звезда головоломка.
• Большой додекаэдр служит простой мнемоникой для двоичный код Голея^[1]

Смотрите также

• Соединение малого звездчатого додекаэдра и большого додекаэдра

Рекомендации

1. * Баэз, Джон "Код Голея," Визуальное понимание, 1 декабря 2015 г.

внешняя ссылка

• Эрик В. Вайсштейн, Большой додекаэдр (Равномерный многогранник ) в MathWorld.
• Вайсштейн, Эрик В. "Три звёздчатых додекаэдра". MathWorld.
• Равномерные многогранники и двойники
• Металлическая скульптура Большого Додекаэдра