Кубогемиоктаэдр - Cubohemioctahedron
| Кубогемиоктаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 10, E = 24 V = 12 (χ = −2) |
| Лица по сторонам | 6{4}+4{6} |
| Символ Wythoff | 4/3 4 | 3 (двойное покрытие) |
| Группа симметрии | Очас, [4,3], *432 |
| Указатель ссылок | U15, C51, W78 |
| Двойной многогранник | Гексагемиоктакрон |
| Фигура вершины |  4.6.4/3.6 |
| Акроним Bowers | Чо |

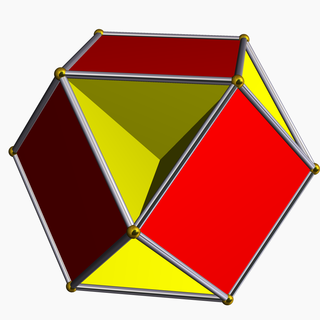
В геометрия, то кубогемиоктаэдр это невыпуклый однородный многогранник, индексируется как U15. Имеет 10 граней (6 квадраты и 4 обычных шестиугольники ), 24 ребра и 12 вершин.[1] Его вершина фигуры это скрещенный четырехугольник.
Дано Символ Wythoff 4⁄3 4 | 3, хотя это двойное покрытие этой фигуры.
Невыпуклый многогранник имеет пересекающиеся грани, которые не представляют новые ребра или грани. На рисунке вершины отмечены золотыми сферами, а края - серебряными цилиндрами.
Это гемиполиэдр с 4 шестиугольник грани, проходящие через центр модели. Шестиугольники пересекаются друг с другом, поэтому видны только треугольные части каждого из них.
Связанные многогранники
Он разделяет расположение вершин и расположение кромок с кубооктаэдр (имеющий общие квадратные грани), и с октагемиоктаэдр (имеющий общие шестиугольные грани).
 Кубооктаэдр |  Кубогемиоктаэдр |  Октагемиоктаэдр |
Тетрагексагональная черепица
В кубогемиоктаэдр можно рассматривать как сеть на гиперболическом тетрагексагональная черепица с вершиной рисунка 4.6.4.6.

Гексагемиоктакрон
| Гексагемиоктакрон | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо | — |
| Элементы | F = 12, E = 24 V = 10 (χ = −2) |
| Группа симметрии | Очас, [4,3], *432 |
| Указатель ссылок | DU15 |
| двойственный многогранник | Кубогемиоктаэдр |
В гексагемиоктакрон является двойником кубогемиоктаэдра и является одним из девяти двойные гемиполиэдры. Он визуально не отличается от октагемиоктакрон.
Поскольку кубогемиоктаэдр имеет четыре гексагональных лица проходя через центр модели, таким образом выродиться, и может рассматриваться как имеющий четыре вершины на бесконечности.
В Магнус Веннингер с Двойные модели, они представлены пересекающимися бесконечными призмы проходя через центр модели, срежьте в удобном для производителя месте.
Смотрите также
- Hemi-cube - Четыре бесконечно удаленные вершины соответствуют четырем вершинам этого абстрактного многогранника.
Рекомендации
- ^ Медер, Роман. "15: кубогемиоктаэдр". MathConsult.
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, МИСТЕР 0730208 (Стр. 101, Двойники (девяти) гемиполиэдров)
внешняя ссылка
- Вайсштейн, Эрик В. «Гексагемиоктакрон». MathWorld.
- Эрик В. Вайсштейн, Кубогемиоктаэдр (Равномерный многогранник ) в MathWorld.
- Равномерные многогранники и двойники
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
