Теорема Котцигса - Kotzigs theorem
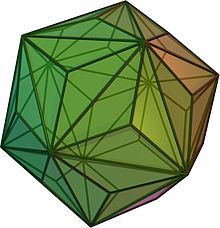
В теория графов и многогранная комбинаторика, области математики, Теорема Коцига утверждение, что каждый многогранный граф имеет край, две конечные точки которого имеют общее степень не более 13. Крайним случаем является триакис икосаэдр, где никакое ребро не имеет меньшей общей степени. Результат назван в честь Антон Коциг, опубликовавший его в 1955 г. в двойной форма, что каждый выпуклый многогранник имеет две смежные грани, всего не более 13 сторон.[1] Он был назван и популяризирован на Западе в 1970-х годах. Бранко Грюнбаум.[2][3]
В более общем смысле, каждый плоский граф минимальной степени не менее трех либо имеет ребро общей степени не более 12, либо не менее 60 ребер, которые (подобно ребрам в триакисикосаэдре) соединяют вершины степеней 3 и 10.[4]Если все треугольные грани многогранника вершинно-непересекающиеся, существует ребро с меньшей общей степенью, не более восьми.[5]Известны также обобщения теоремы вложения графов на поверхности с более высокими род.[6]
Теорема не может быть обобщена на все планарные графы, как полные двудольные графы и имеют ребра с неограниченной суммарной степенью. Однако для плоских графов с вершинами степени ниже трех были доказаны варианты теоремы, показывающие, что существует либо ребро ограниченной полной степени, либо подграф другого особого вида.[7]
Рекомендации
- ^ Коциг, Антон (1955), "Вклад в теорию многогранников Эйлера", Matematicko-Fyzikálny Časopis, 5: 101–113, МИСТЕР 0074837
- ^ Грюнбаум, Бранко (1975), "Многогранные графы", Исследования по теории графов, часть II, MAA Исследования по математике, 12, стр. 201–224, МИСТЕР 0406868
- ^ Грюнбаум, Бранко (1976), "Новые взгляды на некоторые старые вопросы комбинаторной геометрии", Colloquio Internazionale sulle Teorie Combinatorie (Рим, 1973), Том I, Atti dei Convegni Lincei, 17, стр. 451–468, МИСТЕР 0470861
- ^ Бородин, О. В. (1990), "Обобщение теоремы Котцига и предписанная раскраска ребер плоских графов", Математические заметки, 48 (6): 22–28, 160, Дои:10.1007 / BF01240258, МИСТЕР 1102617
- ^ Бородин, Олег В. (1992), "Расширение теоремы Котцига о минимальном весе ребер в 3-многогранниках", Mathematica Slovaca, 42 (4): 385–389, МИСТЕР 1195032
- ^ Закс, Джозеф (1983), "Расширение теоремы Коцига", Израильский математический журнал, 45 (4): 281–296, Дои:10.1007 / BF02804013, HDL:10338.dmlcz / 127504, МИСТЕР 0720304
- ^ Коул, Ричард; Ковалик, Лукаш; Шкрековски, Ристе (2007), «Обобщение теоремы Коцига и его применение», Журнал SIAM по дискретной математике, 21 (1): 93–106, CiteSeerX 10.1.1.227.3878, Дои:10.1137/050646196, МИСТЕР 2299697


