Пентаграмматический куплоид - Pentagrammic cuploid
| Пентаграмматический куплоид | |
|---|---|
 | |
| Тип | Куплоид |
| Лица | 5 треугольники 5 квадраты 1 пентаграмма |
| Края | 20 |
| Вершины | 10 |
| Конфигурация вершины | 5(5/2.4.3.4) 5(3.4.3/2.4/3) |
| Группа симметрии | C5в, [5], (*55) |
| Группа вращения | C5, [5]+, (55) |
| Двойной многогранник | Пентаграмматический кератиноид |
| Характеристики | неориентируемый имеет мембрану |

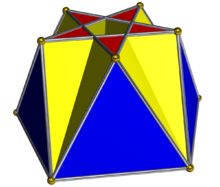
В геометрия, то пентаграмматический куплоид или же пентаграммическая полукупола самый простой из бесконечного семейства куплоиды. Его можно получить как кусок малый сложный ромбикосододекаэдр. Как и во всех купола, база многоугольник вдвое больше края и вершины как верхний; но в этом случае базовый многоугольник является вырожденным {10/2} декаграмма, так как верх - это {5/2} пентаграмма. Следовательно, вырожденное основание удаляется, и вместо этого треугольники соединяются с квадратами.
Связанные многогранники
| п⁄d | 3 | 5 | 7 |
|---|---|---|---|
| 2 |  Перекрещенный треугольный куплоид |  Пентаграмматический куплоид |  Гептаграмматический куплоид |
| 4 | — |  Перекрещенный пятиугольный куплоид |  Скрещенный гептаграммный куплоид |
Пентаграмматический куплоид можно рассматривать как часть вырожденного однородного многогранника, известного как малый сложный ромбикосододекаэдр:
 Пентаграмматический куплоид | 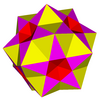 Малый сложный ромбикосододекаэдр | ||
 Малый дитригональный икосододекаэдр |  Дитригональный додекадодекаэдр |  Большой дитригональный икосододекаэдр |  Соединение пяти кубиков |
(На изображении пентаграммы куплоида пентаграмма красная, квадраты - желтые, а треугольники - синие. На изображении небольшого сложного ромбикосододекаэдра пентаграммы розовые, квадраты красные, а треугольники желтые. пентаграммы были удалены, поскольку в противном случае красные квадраты небольшого сложного ромбикосододекаэдра были бы невидимы.)
Если взять одну пентаграмму из небольшого сложного ромбикосододекаэдра, затем взять пять соседних с ней квадратов, затем взять пять треугольников, которые граничат с этими квадратами, получится пентаграмматический куплоид. Так как этот пентаграмматический куплоид, таким образом, разделяет все свои края с этим многогранником, его можно назвать край-огранка этого. Невырожденные однородные многогранники, имеющие те же ребра, что и небольшой сложный ромбикосододекаэдр, представляют собой три дитригональные многогранники, а также обычный соединение пяти кубиков: следовательно, пентаграмматический куплоид также является гранью этих многогранников.
В качестве 5/2 > 2, треугольники и квадраты не полностью закрывают нижнюю часть пентаграмматического куплоида, и, следовательно, центр пентаграммического основания доступен с обеих сторон и не закрывает никакого пространства. Следовательно, это мембрана, и она не была заполнена на приведенной выше иллюстрации многогранника, так как ее заполнение означало бы, что плотности на любой пентаграмме различаются, когда они обе равны 0. Было высказано предположение, что многогранник с 10 или менее гранями не может иметь мембраны: пентаграмматический куплоид имеет 11 граней.
Двойной многогранник

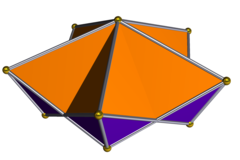
Двойник пентаграмматического куплоида имеет 5 воздушных змеев и 5 воздушных змеев. антипараллелограмм лица, и был назван пентаграмматический кератиноид от Inchbald, поскольку он имеет форму полого рога:
Рекомендации
- Гай Инчбальд, Заполнение многогранников
- Ричард Клитцинг, Осесимметричные грани равномерных многогранников.
- Ричард Клитцинг, Гранки однородных многогранников (Ведущий и представленный Ульрихом Микловейтом)
- Джим Макнил, Полукупола 5/2 и полукупола 5/4
- Джим Макнил, Полукупола
