Тетрагональный трапецоэдр - Tetragonal trapezohedron

Тетрагональный трапецоэдр
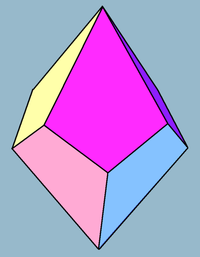Тетрагональный трапецоэдр
Нажмите на картинку для увеличения.
Типтрапецоэдры
КонвейdA4
Диаграмма КокстераCDel узел fh.pngCDel 2x.pngCDel узел fh.pngCDel 8.pngCDel node.png
CDel узел fh.pngCDel 2x.pngCDel узел fh.pngCDel 4.pngCDel узел fh.png
Лица8 воздушные змеи
Края16
Вершины10
Конфигурация лицаV4.3.3.3
Группа симметрииD4d, [2+, 8], (2 * 4), порядок 16
Группа вращенияD4, [2,4]+, (224), заказ 8
Двойной многогранникКвадратная антипризма
Характеристикивыпуклый, лицо переходный

В четырехугольный трапецоэдр, или же дельтоэдр, является вторым в бесконечной серии однородных по граням многогранников, которые двойной к антипризмы. У него восемь граней, которые конгруэнтный воздушные змеи, и двойственен квадратная антипризма.

В генерации сетки

Эта форма использовалась как тестовый пример для гексаэдрической создание сетки,[1][2][3][4][5] упрощая предыдущий тестовый пример, предложенный математиком Робертом Шнайдером в форме квадратная пирамида с границей, разделенной на 16 четырехугольников. В этом контексте тетрагональный трапецоэдр также получил название кубический октаэдр,[3] четырехугольник октаэдр,[4] или же восьмиугольный шпиндель,[5] потому что он имеет восемь четырехугольных граней и однозначно определяется как комбинаторный многогранник этим свойством.[3] Добавление четырех кубоидов к сетке для кубического октаэдра также даст сетку для пирамиды Шнайдера.[2] Как односвязный многогранник с четным числом четырехугольников, кубический октаэдр можно разложить на топологические кубоиды с криволинейными гранями, пересекающимися лицом к лицу, без разделения граничных четырехугольников,[1][5][6] и была построена явная сетка этого типа.[4] Однако неясно, можно ли получить такое разложение, в котором все кубоиды представляют собой выпуклые многогранники с плоскими гранями.[1][5]

Связанные многогранники

Семья п-гональный трапецоэдры
Изображение многогранникаDigonal trapezohedron.pngTrigonalTrapezohedron.svgТетрагональный трапецоэдр.pngПятиугольный трапецииэдр.svgШестиугольный трапецоэдр.pngШестиугольный трапецииэдр.pngOctagon trapezohedron.pngДесятиугольный трапецииэдр.pngДодекагональный трапецииэдр.png...Апейрогональный трапецоэдр
Сферическое мозаичное изображениеСферическая двуугольная антипризма.pngСферический треугольник trapezohedron.pngСферический тетрагональный трапецоэдр.pngСферический пятиугольник trapezohedron.pngСферический шестиугольный трапецииэдр.pngСферический семиугольник trapezohedron.pngСферический восьмиугольник trapezohedron.pngСферический десятиугольный трапецоэдр.pngСферический двенадцатигранник trapezohedron.pngПлоское мозаичное изображениеАпейрогональный трапецоэдр.svg
Конфигурация лица Vп.3.3.3V2.3.3.3V3.3.3.3V4.3.3.3V5.3.3.3V6.3.3.3V7.3.3.3V8.3.3.3V10.3.3.3V12.3.3.3...V∞.3.3.3

В тетрагональный трапецииэдр является первым в серии двойственных курносых многогранников и мозаик с конфигурация лица V3.3.4.3.п.

Рекомендации

  1. ^ а б c Эппштейн, Дэвид (1996), "Построение шестигранной сетки линейной сложности", Материалы двенадцатого ежегодного симпозиума по вычислительной геометрии (SCG '96), Нью-Йорк, Нью-Йорк, США: ACM, стр. 58–67, arXiv:cs / 9809109, Дои:10.1145/237218.237237, МИСТЕР  1677595, S2CID  3266195.
  2. ^ а б Митчелл, С. А. (1999), «Шестигранный геодезический шаблон для согласования нарезанной кубиками четырехгранной сетки с любой нарезанной кубиками шестигранной сетки», Разработка с помощью компьютеров, 15 (3): 228–235, Дои:10.1007 / s003660050018, S2CID  3236051.
  3. ^ а б c Шварц, Александр; Циглер, Гюнтер М. (2004), «Техника построения кубических комплексов, нечетных кубических 4-многогранников и заданных двойственных многообразий», Экспериментальная математика, 13 (4): 385–413, Дои:10.1080/10586458.2004.10504548, МИСТЕР  2118264, S2CID  1741871.
  4. ^ а б c Carbonera, Carlos D .; Шеперд, Джейсон Ф .; Шеперд, Джейсон Ф. (2006 г.), «Конструктивный подход к созданию гексаэдральной сетки с ограничениями», Материалы 15-го Международного круглого стола по сетке, Берлин: Springer, стр. 435–452, Дои:10.1007/978-3-540-34958-7_25.
  5. ^ а б c d Эриксон, Джефф (2013), "Эффективное создание шестнадцатеричных сетей с помощью топологии", Материалы двадцать девятого ежегодного симпозиума по вычислительной геометрии (SoCG '13) (PDF), Нью-Йорк, Нью-Йорк, США: ACM, стр. 37–46, Дои:10.1145/2462356.2462403, S2CID  10861924.
  6. ^ Митчелл, Скотт А. (1996), "Характеристика четырехугольных сеток поверхности, которые допускают совместимую шестигранную сетку замкнутого объема", STACS 96: 13-й ежегодный симпозиум по теоретическим аспектам компьютерных наук Гренобль, Франция, 22–24 февраля 1996 г., Материалы, Конспект лекций по информатике, 1046, Берлин: Springer, стр. 465–476, Дои:10.1007/3-540-60922-9_38, МИСТЕР  1462118.

внешняя ссылка