Звездчатый октаэдр - Stellated octahedron
| Звездчатый октаэдр | |
|---|---|
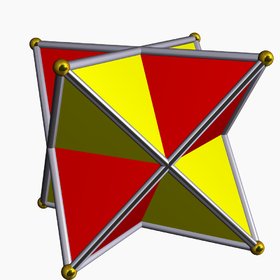 Рассматривается как соединение двух правильных тетраэдров (красного и желтого) | |
| Тип | Обычное соединение |
| Символ Кокстера | {4,3}[2{3,3}]{3,4}[1] |
| Символы Шлефли | {{3,3}} а {4,3} ß {2,4} ßr {2,2} |
| Диаграммы Кокстера | |
| Звездчатость основной | Октаэдр |
| Выпуклый корпус | Куб |
| Индекс | UC4, W19 |
| Многогранники | 2 тетраэдры |
| Лица | 8 треугольники |
| Края | 12 |
| Вершины | 8 |
| Двойной | Самодвойственный |
| Группа симметрии Группа Коксетера | Очас, [4,3], порядок 48 D4ч, [4,2], порядок 16 D2ч, [2,2], порядок 8 D3D, [2+, 6], порядок 12 |
| Подгруппа ограничение одной составляющей | Тd, [3,3], порядок 24 D2d, [2+, 4], порядок 8 D2, [2,2]+, заказ 4 C3в, [3], порядок 6 |
В звездчатый октаэдр единственный звездчатость из октаэдр. Его еще называют Stella Octangula (На латыни «восьмиконечная звезда»), имя, данное ей Иоганн Кеплер в 1609 г., хотя раньше было известно геометры. Он был изображен в Пачоли с De Divina Proportione, 1509.[2]
Это самый простой из пяти обычных полиэдрические соединения, и единственный регулярный соединение двух тетраэдров. Это также наименее плотное из обычных полиэдрических соединений, имеющее плотность 2.
Его можно рассматривать как трехмерное расширение гексаграмма: гексаграмма представляет собой двумерную фигуру, образованную двумя перекрывающимися равносторонними треугольниками, центрально-симметричный друг к другу, и таким же образом звездчатый октаэдр может быть образован из двух центрально-симметричных перекрывающихся тетраэдров. Это можно обобщить на любое желаемое количество более высоких измерений; четырехмерная эквивалентная конструкция - это соединение двух 5-ти ячеек. Также это можно рассматривать как один из этапов построения 3D Коха снежинка, фрактальная форма, образованная повторным присоединением меньших тетраэдров к каждой треугольной грани большей фигуры. Первый этап построения Снежинки Коха - это единственный центральный тетраэдр, а второй этап, образованный добавлением четырех меньших тетраэдров к граням центрального тетраэдра, - это звездчатый октаэдр.
Строительство
Декартовы координаты звездчатого октаэдра следующие: (± 1/2, ± 1/2, 0) (0, 0, ± 1 / √2) (± 1, 0, ± 1 / √2) (0, ± 1, ± 1 / √2)
Звездчатый октаэдр можно построить несколькими способами:
- Это звездчатость из правильный октаэдр, разделяющие те же плоскости лица. (Видеть Веннингера модель W19.)
 В перспективе |  Звездчатая плоскость | Единственная звездчатая форма правильного октаэдра с одной звездчатой плоскостью желтого цвета. |
- Это также обычный соединение многогранника, будучи построенным как объединение двух регулярных тетраэдры (правильный тетраэдр и его двойственный тетраэдр ).
- Его можно получить как увеличение регулярного октаэдр, добавив тетраэдрический пирамиды на каждом лице. В этой конструкции он имеет ту же топологию, что и выпуклый Каталонский твердый, то триакис октаэдр, пирамиды которого намного короче.
- Это огранка из куб, разделяя расположение вершин.
- Это можно рассматривать как {4/2} антипризма; где {4/2} представляет собой тетраграмму, соединение двух двойных дигоны, и тетраэдр, рассматриваемый как двуугольная антипризма, это можно рассматривать как соединение двух дигональные антипризмы.
- Это можно рассматривать как сеть четырехмерного восьмигранная пирамида, состоящий из центрального октаэдра, окруженного восемью тетраэдрами.
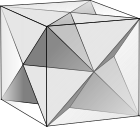 Огранка куба | 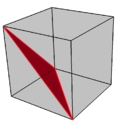 Одиночный диагональный треугольник, ограненный красным |
Связанные понятия

Соединение двух сферических тетраэдров может быть построено, как показано.
Два тетраэдра составного вида звездчатого октаэдра являются «десмическими», что означает, что (при интерпретации как линия в проективное пространство ) каждое ребро одного тетраэдра пересекает два противоположных ребра другого тетраэдра. Одно из этих двух пересечений видно в звездчатом октаэдре; другое пересечение происходит в бесконечно удаленной точке проективного пространства между двумя параллельными ребрами двух тетраэдров. Эти два тетраэдра можно дополнить до десмическая система трех тетраэдров, где третий тетраэдр имеет четыре вершины, три бесконечно удаленных точки пересечения и центроид двух конечных тетраэдров. Те же двенадцать вершин тетраэдра также образуют точки Конфигурация Рея.
В числа stella octangula находятся фигуральные числа которые подсчитывают количество шаров, которые можно расположить в форме звездчатого октаэдра. Они есть
В популярной культуре
Звездчатый октаэдр появляется с несколькими другими многогранниками и полиэдрическими соединениями в М. К. Эшер печать "Звезды ",[3] и представляет собой центральную форму в книге Эшера Двойной планетоид (1949).[4]
Некоторые современные мистики связывают эту форму с «меркабой»,[5] что, по их мнению, является «противоположно вращающимся энергетическим полем», названным от древнеегипетского слова.[6]Однако слово «меркаба» на самом деле иврит, а точнее относится к колесница в видениях Иезекииль.[7]Сходство этой формы с двухмерным звезда Давида также часто отмечалось.[8]
Звездчатый октаэдр также является общей формой дрона "Призрак", найденного в видеоигре. Судьба.
Галерея
 |  |  |
 |  |  |
Рекомендации
- ^ H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, 3.6 Пять обычных соединений, стр.47-50, 6.2 Звездчатые тела Платоновых тел, стр.96-104
- ^ Барнс, Джон (2009), «Фигуры и твердые тела», Самоцветы геометрии, Springer, стр. 25–56, Дои:10.1007/978-3-642-05092-3_2, ISBN 978-3-642-05091-6.
- ^ Харт, Джордж У. (1996), "Многогранники М. К. Эшера", Виртуальные многогранники.
- ^ Кокстер, Х. С. М. (1985), "Специальная рецензия на книгу: М. К. Эшер: Его жизнь и полная графическая работа", Математический интеллект, 7 (1): 59–69, Дои:10.1007 / BF03023010. См., В частности, стр. 61.
- ^ Даннелли, Ричард (1995), Седона: За пределами вихря: активация программы вознесения планет с помощью сакральной геометрии, вихря и Меркабы, Издательство «Световые технологии», стр. 14, ISBN 9781622336708
- ^ Мелхиседек, Друнвало (2000), Древний секрет Цветка Жизни: Отредактированная стенограмма семинара «Цветок Жизни», представленного в прямом эфире Матери Земле с 1985 по 1994 - Том 1, Издательство «Световые технологии», стр. 4, ISBN 9781891824173
- ^ Патция, Артур Дж .; Петротта, Энтони Дж. (2010), Карманный словарь библейских исследований: более 300 терминов с четким и кратким определением, Серия карманных справочников IVP, InterVarsity Press, стр. 78, ISBN 9780830867028
- ^ Бриссон, Дэвид В. (1978), Гиперграфика: визуализация сложных отношений в искусстве, науке и технологиях, Westview Press для Американской ассоциации содействия развитию науки, стр. 220,
Стелла octangula - 3-й аналог Звезды Давида.
