Омар Хайям - Omar Khayyam
Омар Хайям عمر خیام | |
|---|---|
 | |
| Родившийся | 18 мая[1] 1048[2] |
| Умер | 4 декабря[1] 1131 (83 года)[2] |
| Национальность | Персидский |
| Школа | Исламская математика, Персидская поэзия, Персидская философия |
Основные интересы | Математика, астрономия, Авиценнизм, поэзия |
Влияния | |
Под влиянием | |
Омар Хайям (/kаɪˈjɑːм/; Персидский: عمر خیّام [oˈmæɾ xæjˈjɒːm]; 18 мая 1048 г. - 4 декабря 1131 г.) Персидский математик, астроном, философ и поэт.[3][4][5][6] Он родился в Нишабур, на северо-востоке Иран, и провел большую часть своей жизни около двора Караханиды и Сельджук правители в период, который засвидетельствовал Первый крестовый поход.
Как математик он наиболее известен своей работой по классификации и решению кубические уравнения, где он дал геометрические решения по пересечению коники.[7] Хайям также внес свой вклад в понимание параллельная аксиома.[8]:284 Как астроном он разработал Календарь Джалали, солнечный календарь с очень точным 33-летним цикл интеркаляции.[9][10]:659
Есть традиция приписывать поэзия Омару Хайяму, написанное в форме катрены (rubāʿiyāt رباعیات). Эта поэзия стала широко известна англоязычному миру в переводе Эдвард Фитцджеральд (Рубайят Омара Хайяма, 1859), который пользовался большим успехом в Ориентализм из Fin de siècle.
Жизнь
Омар Хайям родился в 1048 году в Нишапуре, ведущем мегаполисе в Хорасан во времена средневековья, который достиг зенита расцвета в одиннадцатом веке при Династия сельджуков.[11]:15[12][13] Нишапур был также крупным центром Зороастрийская религия, и вполне вероятно, что отец Хайяма был зороастрийцем, обратившимся в ислам.[14]:68 Его полное имя, как следует из арабских источников, было Абу'л Фатх Омар ибн Ибрагим аль-Хайям.[15]В средневековых персидских текстах его обычно называют просто Омар Хайям.[16] Хотя это вызывает сомнения, часто предполагалось, что его предки занимались изготовлением палаток, поскольку Хайям средства палатка по-арабски.[17]:30 Историк Байхаки, который был лично знаком с Омаром, приводит полную информацию о его гороскопе: «он был Близнецами, Солнце и Меркурий были в асценденте [...]».[18]:471 Современные ученые установили дату его рождения 18 мая 1048 года.[10]:658

Его детство прошло в Нишапуре.[10]:659 Его дары были признаны его ранними наставниками, которые отправили его учиться у Имама Муваффака Нишабури, величайшего учителя региона Хорасан, который обучал детей высшей знати.[14]:20 Хайям также обучал обращенный зороастрийский математик, Абу Хасан Бахманьяр бин Марзбан.[19] Изучив естественные науки, философию, математику и астрономию в Нишапуре, около 1068 года он отправился в провинцию Бухара, где он часто посещал знаменитую библиотеку Ковчега. Примерно в 1070 году он переехал в Самарканд, где он начал сочинять свои знаменитые трактат по алгебре под покровительством Абу Тахира Абд ар-Рахмана ибн Алака, губернатора и главный судья города.[20] Омара Хайяма любезно принял правитель Караханидов Шамс аль-Мульк Наср, который, согласно Байхаки, «окажет ему величайшую честь, настолько, что он усадит [Омара] рядом с собой на свою трон ".[17]:34[14]:47
В 1073-104 был заключен мир с Султан Малик-Шах I которые совершали вторжения в владения Караханидов. Хайям поступил на службу к Малик-шаху в 1074-105 годах, когда его пригласил Великий визирь Низам аль-Мульк встретить Малик-Шаха в городе Марв. Впоследствии Хайяму было поручено создать обсерваторию в Исфахан и возглавил группу ученых в проведении точных астрономических наблюдений, направленных на пересмотр персидского календаря. Предприятие началось, вероятно, в 1076 году и закончилось в 1079 году.[14]:28 когда Омар Хайям и его коллеги завершили свои измерения длины года, сообщив об этом 14 значимым цифрам с поразительной точностью.
После смерти Малик-шаха и его визиря (убитых, как полагают, Исмаилиты орден ассасинов ), Омар попал в немилость при дворе, и в результате вскоре он паломничество в Мекку. Возможный скрытый мотив его паломничества сообщил Аль-Кифти, была публичной демонстрацией его веры с целью развеять подозрения в скептицизме и опровергнуть утверждения о неортодоксальности (включая возможное сочувствие зороастризму), выдвинутые в его адрес враждебным духовенством.[21][14]:29 Затем он был приглашен новым Султан Санджар Марву, возможно, работать в суде астролог.[1] Позже ему разрешили вернуться в Нишапур из-за ухудшения его здоровья. По возвращении он, похоже, жил жизнью отшельника.[22]:99
Омар Хайям умер в возрасте 83 лет в своем родном городе Нишапур 4 декабря 1131 года, и он похоронен на том месте, где сейчас находится Мавзолей Омара Хайяма. Один из его учеников Низами Арузи рассказывает историю о том, что когда-то в 1112-11 годах Хайям был в Балх в компании Аль-Исфизари (один из ученых, сотрудничавших с ним по календарю Джалали), когда он сделал пророчество о том, что «моя могила будет в месте, где северный ветер может рассыпать розы».[17]:36[12] Через четыре года после своей смерти Арузи обнаружил свою могилу на кладбище в тогдашнем большом и известном квартале Нишапура по дороге в Марв. Как и было предвидено Хайямом, Арузи нашел гробницу у подножия садовой стены, над которой грушевые и персиковые деревья склонили головы и уронили свои цветы, так что его могильный камень был скрыт под ними.[17]
Математика
Хайям был известен при жизни как математик. Его сохранившиеся математические работы включают: Комментарий к трудностям, связанным с постулатами Элементов Евклида. (Рисала фи шарм ма ашкала мин мунадарат китаб Уклидис, завершено в декабре 1077 г.[6]), О разделении квадрант круга (Рисала фи кисмах руб аль-даира, без даты, но завершено до трактата по алгебре[6]), и О доказательствах задач алгебры (Макала фи ль-джабр ва ль-мукабала, скорее всего завершено в 1079 г.[8]:281). Кроме того, он написал трактат по извлечению биномиальная теорема и пth корень натуральных чисел, которое было потеряно.[14]:197
Теория параллелей
Часть комментария Хайяма к Элементам Евклида посвящена параллельная аксиома.[8]:282 Трактат Хайяма можно считать первой трактовкой аксиомы, не основанной на Petitio Principii, но на основе более интуитивного постулата. Хайям опровергает предыдущие попытки других математиков доказывать предположение, главным образом на том основании, что каждый из них постулировал что-то, что было отнюдь не легче принять, чем сам Пятый постулат.[6] Опираясь на Аристотель точки зрения, он отвергает использование движения в геометрии и, следовательно, отклоняет различные попытки Аль-Хайтам.[23][24] Неудовлетворенный тем, что математики не смогли доказать утверждение Евклида на основе других его постулатов, Омар попытался связать аксиому с Четвертым постулатом, в котором говорится, что все прямые углы равны друг другу.[8]:282
Хайям был первым, кто рассмотрел три случая острого, тупого и прямого угла для вершинных углов Четырехугольник Хайям-Саккери, три случая, которые являются исчерпывающими и попарно взаимоисключающими.[8]:283 Доказав ряд теорем о них, он доказал, что постулат V является следствием гипотезы прямого угла, и отверг тупые и острые случаи как противоречащие самому себе.[6] Сложная попытка Хайяма доказать постулат параллельности была значимой для дальнейшего развития геометрии, поскольку она ясно показывает возможность неевклидовых геометрий. Теперь известно, что гипотезы острого, тупого и прямого угла приводят, соответственно, к неевклидовой теории. гиперболическая геометрия Гаусс-Бояи-Лобачевского, к Риманова геометрия, и чтобы Евклидова геометрия.[25]

Туси Комментарии по поводу трактовки Хайямом параллелей дошли до Европы. Джон Уоллис, профессор геометрии в Оксфорде, перевел комментарий Туси на латынь. Иезуитский геометр Джироламо Саккери, чьи работы (euclides ab omni naevo vindicatus, 1733) обычно рассматривается как первый шаг в конечном развитии неевклидова геометрия, был знаком с творчеством Уоллис. Американский историк математики, Дэвид Юджин Смит, упоминает, что Саккери «использовал ту же лемму, что и лемму Туси, даже обозначая фигуру точно таким же образом и используя лемму для той же цели». Далее он говорит, что «Туси четко заявляет, что это связано с Омаром Хайямом, и из текста становится ясно, что последний был его вдохновителем».[22]:104[26][14]:195
Концепция действительного числа
Этот трактат о Евклиде содержит еще один вклад, посвященный теория пропорций и с составлением соотношений. Хайям обсуждает взаимосвязь между концепцией отношения и концепцией числа и явно поднимает различные теоретические трудности. В частности, он вносит свой вклад в теоретическое изучение концепции иррациональный номер.[6] Недовольный определением равных соотношений Евклидом, он переопределил понятие числа, использовав непрерывную дробь как средство выражения отношения. Розенфельд и Юшкевич (1973) утверждают, что «поместив иррациональные количества и числа в одну и ту же операционную шкалу, [Хайям] начал настоящую революцию в доктрине числа». Точно так же это было отмечено Д. Дж. Струик что Омар был «на пути к тому расширению концепции числа, которое ведет к понятию настоящий номер."[8]:284
Геометрическая алгебра

Рашед и Вахабзаде (2000) утверждали, что благодаря его основательному геометрическому подходу к алгебраическим уравнениям Хайяма можно считать предшественником Декарт в изобретении аналитическая геометрия.[27]:248 В Трактат о делении квадранта круга Хайям применил алгебру к геометрии. В этой работе он в основном посвятил себя исследованию возможности разделить круговой квадрант на две части так, чтобы отрезки прямых, спроецированные из точки разделения на диаметры перпендикуляра круга, образовывали определенное соотношение. В его решении, в свою очередь, использовалось несколько построений кривых, которые приводили к уравнениям, содержащим кубические и квадратичные члены.[27]:248
Решение кубических уравнений
Хайям, кажется, был первым, кто задумал общую теорию кубических уравнений.[28] и первый, кто геометрически решает все типы кубических уравнений в том, что касается положительных корней.[29] Трактат по алгебре содержит его работы по кубические уравнения.[30] Он разделен на три части: (i) уравнения, которые можно решить с помощью компас и линейка, (ii) уравнения, которые можно решить с помощью конические секции, и (iii) уравнения, которые включают обратный неизвестного.[31]
Хайям составил исчерпывающий список всех возможных уравнений, включающих прямые, квадраты и кубы.[32]:43 Он рассмотрел три биномиальных уравнения, девять трехчленных уравнений и семь тетраноминальных уравнений.[8]:281 Для многочленов первой и второй степени он предоставил численные решения с помощью геометрического построения. Он пришел к выводу, что существует четырнадцать различных типов кубиков, которые нельзя свести к уравнению меньшей степени.[6] Для этого он не мог построить свой неизвестный сегмент с помощью компаса и линейки. Он приступил к представлению геометрических решений всех типов кубических уравнений, используя свойства конических сечений.[33]:157[8]:281 Предварительные леммы для геометрического доказательства Хайяма включают Евклид VI, Предложение 13 и Аполлоний II, Опора 12.[33]:155 Положительный корень кубического уравнения определялся как абсцисса точки пересечения двух коник, например, пересечения двух параболы, или пересечение параболы и круга и т. д.[34]:141 Однако он признал, что арифметическая проблема этих кубиков все еще не решена, добавив, что «возможно, кто-то еще узнает об этом после нас».[33]:158 Эта задача оставалась открытой до XVI века, когда алгебраическое решение кубического уравнения было найдено в его общности с помощью Кардано, Дель Ферро, и Тарталья в Ренессанс Италия.[8]:282[6]
Омар Хайям[35]
По сути, работа Хайяма - это попытка объединить алгебру и геометрию.[36]:241 Это конкретное геометрическое решение кубических уравнений было дополнительно исследовано М. Хахтруди и распространен на решение уравнений четвертой степени.[37] Хотя подобные методы периодически появлялись с тех пор, как Менахм, и далее развитый математиком 10-го века Абу аль-Джуд,[38][39] Работу Хайяма можно считать первым систематическим исследованием и первым точным методом решения кубических уравнений.[40] Математик Woepcke (1851), предложивший переводы алгебры Хайяма на французский язык, похвалил его за «силу обобщения и его строго систематическую процедуру».[41]:10
Биномиальная теорема и извлечение корней
Омар Хайям Трактат о демонстрации задач алгебры[42]
В своем алгебраическом трактате Хайям ссылается на книгу, которую он написал об извлечении корень числа-го числа, используя обнаруженный им закон, не зависящий от геометрических фигур.[34] Эта книга, скорее всего, называлась Трудности арифметики (Мошкелат аль-Хесаб),[6] и не сохранился. Исходя из контекста, некоторые историки математики, такие как Д. Дж. Струик, полагают, что Омар должен был знать формулу расширения бинома. , куда п положительное целое число.[8]:282 Случай степени 2 явно указан в элементах Евклида, а случай максимальной степени 3 был установлен индийскими математиками. Хайям был математиком, который заметил важность общей биномиальной теоремы. Аргумент, подтверждающий утверждение, что Хайям имел общую биномиальную теорему, основан на его способности извлекать корни.[43] Один из предшественников Хайяма, Аль-Караджи, уже открыл треугольное расположение коэффициентов биномиального разложения, которое европейцы позже стали называть Треугольник Паскаля;[44] Хайям популяризировал это треугольная решетка в Иране, так что теперь он известен как треугольник Омара Хайяма.[34]
Астрономия
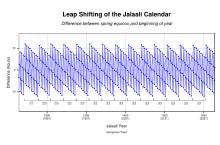
В 1074-105 Султан Малик-Шах поручил Омару Хайяму построить обсерватория в Исфахане и реформировать Персидский календарь. Под руководством Хайяма работала группа из восьми ученых, которая проводила крупномасштабные астрономические наблюдения и пересматривала астрономические таблицы.[34]:141 Перекалибровка календаря зафиксировала первый день года в точный момент прохождения центра Солнца. весеннее равноденствие. Это знаменует начало весны или Новруз, день, когда Солнце входит в первую степень Овен до полудня.[45][46] Получившийся календарь был назван в честь Малик-Шаха как Календарь Джалали, и был открыт 15 марта 1079 г.[47] В обсерватория сама была заброшена после смерти Малик-шаха в 1092 году.[10]:659
Календарь Джалали был истинным солнечный календарь где продолжительность каждого месяца равна времени прохождения Солнца через соответствующий знак Зодиак. Календарная реформа ввела уникальный 33-летний вставка цикл. На что указывают работы Хазини, Группа Хайяма внедрила систему интеркаляции на основе четырехлетних и пятилетних високосные годы. Таким образом, календарь состоял из 25 обыкновенных лет, включающих 365 дней, и 8 високосных лет, включающих 366 дней.[48] Календарь оставался в употреблении Большой Иран с 11 по 20 вв. В 1911 году календарь Джалали стал официальным национальным календарем Каджар Иран. В 1925 году этот календарь был упрощен, а названия месяцев были модернизированы, в результате чего современный иранский календарь. Календарь Джалали более точен, чем Григорианский календарь 1582 г.,[10]:659 с погрешностью в один день, накопленный за 5000 лет, по сравнению с одним днем каждые 3330 лет по григорианскому календарю.[14]:200Мориц Кантор считал его самым совершенным календарем из когда-либо созданных.[22]:101
Один из его учеников Низами Арузи из Самарканда сообщает, что Хайям, по-видимому, не верил в астрологию и гадания: «Я не заметил, чтобы он (scil. Омар Хайям) сильно верил в астрологические предсказания, и я не видел и не слышал ни о ком из великих [ученых], которые верили в такую веру ».[41]:11 Когда он работал астрологом на Султана Санджара, его попросили предсказывать погоду - работа, которую он, по-видимому, не делал хорошо.[14]:30 Джордж Салиба (2002) объясняет, что термин ‘Илм ан-нуджум, используемый в различных источниках, в которых можно найти ссылки на жизнь и деятельность Омара, иногда неправильно переводился как означающий астрологию. Он добавляет: «по крайней мере, с середины десятого века, согласно Фараби перечисление наук, что эта наука, ‘Илм ан-нуджум, уже был разделен на две части, одна касалась астрологии, а другая - теоретической математической астрономии ».[49]:224
Популярное утверждение о том, что Хайям верил в гелиоцентризм основан на Эдвард Фитцджеральд популярная, но анахронистическая интерпретация поэзии Хайяма, в которой первые строки неправильно переведены с гелиоцентрическим изображением Солнца, бросающего «Камень, обращающий звезды в полет». Фактически, самая популярная версия перевода Фитцджеральда первых строк «Рубайят» Хайяма - «Пробудитесь! Утро в чашу ночи швырнуло камень, обращающий звезды в бегство». [50][51]
Другие работы
У него есть небольшой трактат, посвященный Принцип архимеда (в полном названии, Об обмане знания двух количеств золота и серебра в соединении, состоящем из двух). Для соединения золота, смешанного с серебром, он описывает метод более точного измерения веса на емкость каждого элемента. Он включает взвешивание компаунда как в воздухе, так и в воде, поскольку вес легче измерить точно, чем объем. Повторяя то же самое и с золотом, и с серебром, можно точно определить, насколько тяжелее воды золото, серебро и соединение. Этот трактат был подробно исследован Эйльхард Видеманн который считал решение Хайяма более точным и сложным, чем решение Хазини и Аль-Найризи кто также занимался этой темой в другом месте.[14]:198
Другой небольшой трактат посвящен теория музыки в котором он обсуждает связь между музыкой и арифметикой. Вклад Хайяма заключался в предоставлении систематической классификации музыкальных гамм и обсуждении математических соотношений между нотами, минорными, мажорными и тетрахорды.[14]:198
Поэзия

Самый ранний намек на поэзию Омара Хайяма принадлежит историку. Имад ад-Дин аль-Исфахани, более молодой современник Хайяма, который прямо идентифицирует его как поэта и ученого (Харидат аль-Каср, 1174).[14]:49[52]:35 Один из самых ранних экземпляров Рубията Омара Хайяма из Фахр ад-Дин Рази. В своей работе Ат-танбих ‘ала баад асрар ал-мав ’дат фил-Коран (ок. 1160 г.), он цитирует одно из своих стихотворений (соответствующее четверостишию LXII первого издания Фитцджеральда). Дайя в его сочинениях (Мирсад аль-Ибад, ок. 1230) цитирует два катрена, один из которых совпадает с тем, что уже сообщил Рази. Дополнительный катрен цитирует историк. Джувайни (Тарих-и Джахангушай, ок. 1226–1283).[52]:36–37[14]:92 В 1340 году Джаджарми включает тринадцать четверостиший Хайяма в свое произведение, содержащее антологию произведений известных персидских поэтов (Мунис аль-ахрар), два из которых до сих пор были известны из более старых источников.[53] Сравнительно поздняя рукопись Бодлианский РС. Ouseley 140, написано на Шираз в 1460 году, который содержит 158 четверостиший на 47 листах. Рукопись принадлежала Уильям Узли (1767–1842) и был приобретен Бодлианской библиотекой в 1844 году.

Время от времени встречаются цитаты из стихов, приписываемых Омару, в текстах, приписываемых авторам XIII и XIV веков, но они также сомнительны в подлинности, поэтому ученые-скептики указывают на то, что вся традиция может быть псевдоэпиграфический.[52]:11
Ганс Генрих Шедер в 1934 году прокомментировал, что имя Омара Хайяма «должно быть вычеркнуто из истории персидской литературы» из-за отсутствия какого-либо материала, который можно было бы с уверенностью отнести к нему. Де Блуа (2004) представляет библиографию рукописной традиции, пессимистично заключив, что ситуация существенно не изменилась со времен Шедера.[54]Пять катренов, позже приписываемых Омару, были обнаружены уже через 30 лет после его смерти, цитируется в Синдбад-Намех. Хотя это устанавливает, что эти конкретные стихи были в обращении во времена Омара или вскоре после этого, это не означает, что эти стихи должны быть его. Де Блуа заключает, что, по крайней мере, процесс приписывания поэзии Омару Хайяму, похоже, начался уже в 13 веке.[55] Эдвард Гранвилл Браун (1906) отмечает трудность отделения подлинных катренов от ложных: «хотя очевидно, что Хайям написал много катренов, вряд ли возможно, за исключением нескольких исключительных случаев, положительно утверждать, что он написал какое-либо из тех, что ему приписывают».[10]:663
В дополнение к персидским катренам, Хайяму приписывают двадцать пять арабских стихов, которые засвидетельствованы такими историками, как аль-Исфахани, Шахразури (Нужат аль-Арва, ок. 1201–1211), Кифти (Тарих аль-Хукама, 1255), и Хамдалла Мустауфи (Тарих-и гузида, 1339).[14]:39
Бойл и Фрай (1975) подчеркивают, что есть ряд других персидских ученых, которые иногда писали катрены, в том числе Авиценна, Газали и Туси. Он приходит к выводу, что также возможно, что поэзия с Хайямом была развлечением его часов досуга: «эти короткие стихи, кажется, часто были работой ученых и ученых, которые сочиняли их, возможно, в моменты расслабления, чтобы назидать или развлекать внутреннее. круг своих учеников ».[10]:662
Поэзия, приписываемая Омару Хайяму, во многом способствовала его популярной известности в современный период, что является прямым результатом чрезвычайной популярности перевода таких стихов на английский язык Эдвард Фитцджеральд (1859 г.). Фитцджеральд Рубайят Омара Хайяма содержит вольные переводы катренов из бодлианской рукописи. Он пользовался таким успехом в Fin de siècle период, когда в библиографии, составленной в 1929 г., было включено более 300 отдельных изданий,[56] и многие другие были опубликованы с тех пор.[57]
Философия

Хайям считал себя интеллектуально учеником Авиценна.[58] По словам Аль-Байхаки, он читал метафизику в книге Авиценны. Книга Исцеления перед тем, как он умер.[10]:661 Считается, что Хайям написал шесть философских работ. Один из них, О существовании (Fi’l-wujūd), первоначально была написана на персидском языке и посвящена предмету существования и его связи с универсалиями. Еще одна статья под названием Необходимость противоречия в мире, детерминизм и существование (Дарурат ат-тадад фил'л-алам ва'ль-джабр ва'л-бака '), написана на арабском языке и имеет свободная воля и детерминизм.[58]:475 Названия других его работ: О бытии и необходимости (Рисала фил-каун ва'л-таклиф), Трактат о трансцендентности в существовании (Аль-Рисала аль-ула филь-вуджуд), О познании универсальных принципов существования (Рисала дар ‘илм куллийат-и вуджуд), и Сокращение относительно природных явлений (Мухтасар фил-Таби'ийят).
Религиозные взгляды
Буквальное прочтение катренов Хайяма приводит к интерпретации его философского отношения к жизни как комбинации пессимизм, нигилизм, эпикурейство, фатализм, и агностицизм.[14]:6[59] Эту точку зрения придерживается Иранологи Такие как Артур Кристенсен, Х. Шедер, Ричард Н. Фрай, Э. Д. Росс,[60]:365 E.H. Whinfield[41]:40 и Джордж Сартон.[11]:18 Напротив, катрены Хайяма также были описаны как мистические Суфий поэзия. Однако это мнение меньшинства ученых.[61] В дополнение к своим персидским катренам Дж. К. Э. Боуэн (1973) упоминает, что арабские стихи Хайяма также «выражают пессимистическую точку зрения, полностью созвучную мировоззрению глубоко вдумчивого философа-рационализма, которым, как известно, был Хайям».[62]:69 Эдвард Фитцджеральд подчеркнул религиозный скептицизм, который он обнаружил в Хайяме.[63] В своем предисловии к Рубайят он утверждал, что его «ненавидели и боялись суфии»,[64] и отрицал всякую претензию на божественную аллегорию: «его вино - настоящий виноградный сок: его таверна, где его нужно было пить: его Саки, Плоть и Кровь, пролившая за него это ".[65]:62 Садех Хедаят является одним из самых известных сторонников философии Хайяма как агностического скептицизма, и, согласно Ян Рыпка (1934), он даже считал Хайяма атеист.[66] Хедаят (1923) утверждает, что «хотя Хайям верит в трансмутацию и преобразование человеческого тела, он не верит в отдельную душу; если нам повезет, частицы нашего тела будут использованы для изготовления кувшина с вином».[67]В более позднем исследовании (1934–35) он далее утверждает, что использование Хайямом суфийской терминологии, такой как «вино», является буквальным, и что он обратился к удовольствия момента как противоядие от его экзистенциальной печали: «Хайям нашел убежище в вине, чтобы отогнать горечь и притупить острие своих мыслей».[68] В этой традиции поэзия Омара Хайяма цитируется в контексте Новый атеизм, например в Портативный атеист к Кристофер Хитченс.[69]
Аль-Кифти (ок. 1172–1248), кажется, подтверждает эту точку зрения на философию Омара.[10]:663 В своей работе История образованных людейон сообщает, что стихи Омара были только внешне в суфийском стиле, но были написаны с антирелигиозной направленностью.[60]:365 Он также упоминает, что в какой-то момент был обвинен в нечестии, но отправился в паломничество, чтобы доказать, что он набожный.[14]:29 Сообщается, что по возвращении в свой родной город он скрывал свои самые глубокие убеждения и вел строго религиозный образ жизни, ходя утром и вечером к месту поклонения.[60]:355
В контексте произведения под названием О познании принципов существованияХайям поддерживает суфийский путь.[14]:8 Чиллик (1960) предполагает, что Омар Хайям видел в суфизме союзника против ортодоксальной религиозности.[70]:75 Другие комментаторы не принимают антирелигиозную направленность поэзии Омара и интерпретируют его упоминания о вине и пьянстве в условном метафорическом смысле, распространенном в суфизме. Французский переводчик Ж. Б. Николя считал, что постоянные призывы Омара пить вино не следует понимать буквально, а следует рассматривать скорее в свете суфийской мысли, где восторженное опьянение «вином» следует понимать как метафору просветленного состояния или божественного состояния. восторг Baqaa.[71] Взгляд Омара Хайяма как суфия защищал Бьеррегор (1915),[72] Идрис Шах (1999),[73] и Дуган (1991), который приписывает репутацию гедонизма недостаткам перевода Фитцджеральда, утверждая, что поэзию Омара следует понимать как «глубоко эзотерическую».[74] С другой стороны, иранские эксперты, такие как Мохаммед Али Форуги и Моджтаба Минови отверг гипотезу о том, что Омар Хайям был суфием.[62]:72 Форуги заявил, что идеи Хайяма, возможно, временами совпадали с идеями суфиев, но нет никаких доказательств того, что он формально был суфием. Аминразави (2007) утверждает, что «суфийское толкование Хайяма возможно только путем прочтения его Rubāʿīyyāt широко и расширяя содержание, чтобы оно соответствовало классической суфийской доктрине ".[14]:128 Более того, Фрай (1975) подчеркивает, что Хайям сильно не любил ряд прославленных суфийских мистиков, принадлежавших к тому же веку. Это включает в себя Шамс Тебризи (духовный наставник Руми ),[14]:58 Наджм ад-Дин Дайя который описал Омара Хайяма как «несчастного философа, атеиста и материалиста»,[62]:71 и Аттар которые считали его не товарищем-мистиком, а свободомыслящим ученым, ожидающим наказания в будущем.[10]:663
Сейед Хоссейн Наср утверждает, что «редуктивно» использовать буквальное толкование его стихов (многие из которых изначально сомнительны) для утверждения философии Омара Хайяма. Вместо этого он приводит толковательный перевод Хайяма Авиценна трактат Беседа о единстве (Аль-Хутбат ат-Таухид), где он выражает ортодоксальные взгляды на Божественное единство по согласованию с автором.[75] Прозаические произведения, предположительно принадлежащие Омару, написаны в Перипатетический стиль и откровенно теистические, имея дело с такими предметами, как существование Бога и теодицея.[14]:160 Как отмечает Боуэн, эти работы указывают на его причастность к проблемам метафизики, а не к тонкостям суфизма.[62]:71 В качестве доказательства веры Хайяма и / или его соответствия исламским обычаям Аминразави упоминает, что в своих трактатах он произносит приветствия и молитвы, восхваляя Бога и Мухаммад. В большинстве биографических отрывков он упоминается с религиозной почетностью, такой как Имам, Покровитель веры (Гийат ад-Дин), и Доказательство истины (Худжат аль-Хакк).[14] Он также отмечает, что биографы, восхваляющие его религиозность, обычно избегают упоминания его стихов, тогда как те, кто упоминает его поэзию, часто не хвалят его религиозный характер.[14]:48 Например, отчет Аль-Байхаки, который на несколько лет предшествует другим биографическим заметкам, говорит об Омаре как об очень набожном человеке, исповедовавшем ортодоксальные взгляды до своего последнего часа.[76]:174
На основании всех существующих текстовых и биографических свидетельств вопрос остается открытым,[14]:11 и в результате Хайям получил резко противоречивые оценки и критику.[60]:350
Прием


Различные биографические выдержки, относящиеся к Омару Хайяму, описывают его как непревзойденного в свое время в научных знаниях и достижениях.[77] Многие называли его эпитетом Король мудрых (арабский: ملك الحکماء).[53]:436[34]:141 Шахразури (ум. 1300) высоко ценит его как математика и утверждает, что его можно рассматривать как «преемника Авиценны в различных областях философского обучения».[60]:352 Аль-Кифти (ум. 1248), хотя и не согласен с его взглядами, признает, что «не имел себе равных в своих познаниях в области естественной философии и астрономии».[60]:355 Несмотря на то, что многие биографы провозгласили его поэтом, по словам Ричард Нельсон Фрай «все еще можно утверждать, что статус Хайяма как первоклассного поэта - сравнительно позднее развитие».[10]:663
Томас Хайд был первым европейцем, который обратил внимание на Омара и перевел одно из его катренов на латынь (Historia Religis veterum Persarum eorumque magorum, 1700).[78]:525 Интерес Запада к Персии вырос с Ориентализм движение в 19 веке. Джозеф фон Хаммер-Пургшталл (1774–1856) перевел некоторые стихи Хайяма на немецкий язык в 1818 году, и Гор Узли (1770–1844) into English in 1846, but Khayyam remained relatively unknown in the West until after the publication of Edward FitzGerald с Rubaiyat of Omar Khayyam in 1859. FitzGerald's work at first was unsuccessful but was popularised by Whitley Stokes from 1861 onward, and the work came to be greatly admired by the Pre-Raphaelites. In 1872 FitzGerald had a third edition printed which increased interest in the work in America. By the 1880s, the book was extremely well known throughout the English-speaking world, to the extent of the formation of numerous "Omar Khayyam Clubs" and a "fin de siècle cult of the Rubaiyat"[79] Khayyam's poems have been translated into many languages; many of the more recent ones are more literal than that of FitzGerald.[80]
FitzGerald's translation was a factor in rekindling interest in Khayyam as a poet even in his native Iran.[81] Sadegh Hedayat в его Songs of Khayyam (Taranehha-ye Khayyam, 1934) reintroduced Omar's poetic legacy to modern Iran. Under the Pahlavi dynasty, a new памятник of white marble, designed by the architect Houshang Seyhoun, was erected over his tomb. A statue by Abolhassan Sadighi was erected in Laleh Park, Тегеран in the 1960s, and a bust by the same sculptor was placed near Khayyam's mausoleum in Nishapur. In 2009, the state of Iran donated a pavilion к United Nations Office in Vienna, inaugurated at Vienna International Center.[82] In 2016, three statues of Khayyam were unveiled: one at the Университет Оклахомы, one in Nishapur and one in Florence, Italy.[83] Over 150 composers have used the Rubaiyat as their source of inspiration. The earliest such composer was Liza Lehmann.[6] The French-Lebanese writer Amin Maalouf based the first half of his historical fiction novel Samarkand on Khayyam's life and the creation of his Rubaiyat.
FitzGerald rendered Omar's name as "Tentmaker", and the anglicized name of "Omar the Tentmaker" resonated in English-speaking popular culture for a while. Таким образом, Nathan Haskell Dole published a novel called Omar, the Tentmaker: A Romance of Old Persia in 1898. Omar the Tentmaker of Naishapur is a historical novel by John Smith Clarke, published in 1910. "Omar the Tentmaker" is also the title of a 1914 play by Richard Walton Tully in an oriental setting, adapted as a silent film in 1922. US General Omar Bradley was given the nickname "Omar the Tent-Maker" in World War II.[84]
В lunar crater Omar Khayyam was named in his honour in 1970, as was the minor planet 3095 Omarkhayyam discovered by Soviet astronomer Lyudmila Zhuravlyova in 1980.[85]
Google released two Google Doodles commemorating him. The first was on his 964th birthday on 18 May 2012. The second was on his 971st birthday on 18 May 2019.[86]

Смотрите также
Цитаты
- ^ а б c "Omar Khayyam (Persian poet and astronomer)". Britannica.com. Получено 30 мая 2012.
- ^ а б Seyyed Hossein Nasr and Mehdi Aminrazavi. An Anthology of Philosophy in Persia, Vol. 1: From Zoroaster to 'Umar Khayyam, I.B. Tauris in association with The Institute of Ismaili Studies, 2007.
- ^ Al-Khalili, Jim (30 September 2010). Pathfinders: The Golden Age of Arabic Science. Penguin UK. ISBN 978-0-14-196501-7.
Later, al-Karkhi, Ibn-Tahir and the great Ibn al-Haytham in the tenth/eleventh century took it further by considering cubic and quartic equations, followed by the Persian mathematician and poet Omar Khayyam in the eleventh century
- ^ Rosenfeld, B. A.; Fouchécour, Ch-H. De (24 April 2012). "ʿUmar K̲h̲ayyam". Encyclopaedia of Islam, Second Edition.
- ^ "Omar Khayyam | Persian poet and astronomer". Encyclopedia Britannica. Получено 13 июля 2018.
Omar Khayyam, Arabic in full Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm al-Nīsābūrī al-Khayyāmī, (born May 18, 1048, Neyshābūr [also spelled Nīshāpūr], Khorāsān [now Iran] – died December 4, 1131, Neyshābūr), Persian mathematician, astronomer, and poet
- ^ а б c d е ж грамм час я j Multiple Authors. "Khayyam, Omar". Encyclopædia Iranica Online. Получено 5 октября 2017.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Omar Khayyam", Архив истории математики MacTutor, University of St Andrews.
- ^ а б c d е ж грамм час я j Struik, D. (1958). “Omar Khayyam, mathematician”. The Mathematics Teacher, 51(4), 280–285.
- ^ With an error of one day accumulating over 5,000 years, it was more precise than the Gregorian calendar of 1582, which has an error of one day in 3,330 years in the Gregorian calendar (Aminrazavi 2007:200).
- ^ а б c d е ж грамм час я j k The Cambridge History of Iran, Volume 4. Cambridge University Press (1975): Richard Nelson Frye
- ^ а б “The Tomb of Omar Khayyâm”, George Sarton, Исида, Vol. 29, No. 1 (Jul. 1938), 15.
- ^ а б Edward FitzGerald, Rubaiyat of Omar Khayyam, Ред. Christopher Decker, (University of Virginia Press, 1997), xv; "The Saljuq Turks had invaded the province of Khorasan in the 1030s, and the city of Nishapur surrendered to them voluntarily in 1038. Thus Omar Khayyam grew to maturity during the first of the several alien dynasties that would rule Iran until the twentieth century.".
- ^ Peter Avery and John Heath-Stubbs, The Ruba'iyat of Omar Khayyam, (Penguin Group, 1981), 14; "These dates, 1048–1031, tell us that Khayyam lived when the Saljuq Turkish Sultans were extending and consolidating their power over Persia and when the effects of this power were particularly felt in Nishapur, Khayyam's birthplace.
- ^ а б c d е ж грамм час я j k л м п о п q р s т ты v ш Mehdi Aminrazavi, The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam, Oneworld Publications (2007)
- ^ in e.g. Al-Qifti (Aminrazavi 2007:55) or Abu'l-Hasan Bayhaqi. (E. D. R., & H. A. R. G. (1929:436).
- ^ Frye (1975:658); e.g. в Rashid-al-Din Hamadani (Browne 1899:409f) or in Munis al-ahrar (Ross 1927:436).
- ^ а б c d Boyle, J. A., Omar Khayyam: astronomer, mathematician and poet, Bulletin of the John Rylands Library. 1969; 52(1):30-45.
- ^ E. D. R., & H. A. R. G. (1929). The Earliest Account of 'Umar Khayyam. Bulletin of the School of Oriental Studies, University of London, 5(3), 467–473.
- ^ "His own man". The Spectator. 21 November 2007. Получено 10 ноября 2019.
- ^ Boris A. Rosenfeld «Umar al-Khayyam» in Helaine Selin, Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer-Verlag, 2008, , p. 2175-2176
- ^ Aminrazavi, Mehdi (2010). "Review of Omar Khayyam: Poet, Rebel, Astronomer". Iranian Studies. 43 (4): 569–571. Дои:10.1080/00210862.2010.495592. ISSN 0021-0862. JSTOR 23033230. S2CID 162241136.
- ^ а б c Great Muslim Mathematicians. Penerbit UTM (July 2000): Mohaini Mohamed
- ^ (Rozenfeld 1988, pp. 64–65)
- ^ (Katz 1998, п. 270). Excerpt: In some sense, his treatment was better than ibn al-Haytham's because he explicitly formulated a new postulate to replace Euclid's rather than have the latter hidden in a new definition.
- ^ Rolwing, R. & Levine, M. (1969). ”The Parallel Postulate”. The Mathematics Teacher, 62(8), 665–669.
- ^ Smith, David (1935). "Euclid, Omar Khayyam and Saccheri," Scripta Mathematica.
- ^ а б Cooper, G. (2003). Journal of the American Oriental Society, 123(1), 248–249.
- ^ "Khayyam biography". www-history.mcs.st-and.ac.uk. Получено 13 июля 2018.
However, Khayyam himself seems to have been the first to conceive a general theory of cubic equations.
- ^ Howard Eves (1958). “Omar Khayyam's Solution of Cubic Equations”, The Mathematics Teacher (1958), pp. 302–303.
- ^ "Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics."Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter, 5 (4): 8–12, Дои:10.2307/3027812, JSTOR 3027812, S2CID 125245433
- ^ Bijan Vahabzadeh,"Khayyam, Omar xv. As Mathematician", Encyclopædia Iranica.
- ^ Netz, R. (1999). “Archimedes Transformed: The Case of a Result Stating a Maximum for a Cubic Equation”. Archive for History of Exact Sciences, 54(1), 1–47.
- ^ а б c Deborah A. Kent, & David J. Muraki (2016). “A Geometric Solution of a Cubic by Omar Khayyam … in Which Colored Diagrams Are Used Instead of Letters for the Greater Ease of Learners”. The American Mathematical Monthly, 123(2), 149–160.
- ^ а б c d е Kennedy, E. (1958). “Omar Khayyam”. The Mathematics Teacher, Vol. 59, No. 2 (1966), pp. 140–142.
- ^ A. R. Amir-Moez, "A Paper of Omar Khayyám", Scripta Mathematica 26 (1963), pp. 323–437
- ^ The Mathematics Teacher, 25(4), 238–241. (1932).
- ^ A. R. Amir-Moez, Khayyam's Solution of Cubic Equations, Mathematics Magazine, Vol. 35, No. 5 (November 1962), pp. 269–271. This paper contains an extension by the late Mohsen Hashtroodi of Khayyam's method to degree four equations.
- ^ Waerden, Bartel L. van der (2013). A History of Algebra: From al-Khwārizmī to Emmy Noether. Springer Science & Business Media. п. 29. ISBN 978-3-642-51599-6.
- ^ Sidoli, Nathan; Brummelen, Glen Van (30 October 2013). From Alexandria, Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J.L. Berggren. Springer Science & Business Media. п. 110. ISBN 978-3-642-36736-6.
- ^ Mathematical Masterpieces: Further Chronicles by the Explorers, п. 92
- ^ а б c E. H. Whinfield, The Quatrains of Omar Khayyam, Psychology Press (2000)
- ^ "Muslim extraction of roots". Mactutor History of Mathematics.
- ^ J. L. Coolidge, The Story of the Binomial Theorem, Amer. Математика. Ежемесячно, Vol. 56, No. 3 (Mar. 1949), pp. 147–157
- ^ Susan Nichols, Al-Karaji: Tenth-Century Mathematician and Engineer, 2017. Rosen Publishing. п. 60
- ^ Akrami, Musa (2011). "The development of Iranian calendar: historical and astronomical foundations". arXiv:1111.4926 [physics.hist-ph ].
- ^ Panaino, A; Abdollahy, R; Balland, D. "Calendars (In the Islamic period)". Encyclopædia Iranica. Получено 21 ноября 2017.
- ^ Farrell, Charlotte (1996), "The ninth-century renaissance in astronomy", The Physics Teacher, 34 (5): 268–272, Bibcode:1996PhTea..34..268F, Дои:10.1119/1.2344432.
- ^ Heydari-Malayeri, M (2004). "concise review of the Iranian calendar". arXiv:astro-ph/0409620.
- ^ Saliba, G. (2002). Iranian Studies, 35(1/3), 220–225.
- ^ Donald and Marilynn Olson (1988). bibcode=1988Obs...108..181O&db_key=AST&page_ind=0&data_type=GIF&type=SCREEN_VIEW&classic=YES “Zodiac Light, False Dawn, and Omar Khayyam”, The Observatory, т. 108, pp. 181–182.
- ^ "Rex Pay". Humanistictexts.org. 2000. Archived from оригинал on 24 March 2012. Получено 8 September 2012.
- ^ а б c Ali Dashti (translated by L. P. Elwell-Sutton), In Search of Omar Khayyam, Routledge Library Editions: Iran (2012)
- ^ а б Edward Denison Ross, Omar Khayyam, Bulletin of the School Of Oriental Studies London Institution (1927)
- ^ Francois De Blois, Persian Literature – A Bio-Bibliographical Survey: Poetry of the Pre-Mongol Period (2004), п. 307.
- ^ Francois De Blois, Persian Literature – A Bio-Bibliographical Survey: Poetry of the Pre-Mongol Period (2004), п. 305.
- ^ Ambrose George Potter, A Bibliography of the Rubaiyat of Omar Khayyam (1929).
- ^ Francois De Blois, Persian Literature – A Bio-Bibliographical Survey: Poetry of the Pre-Mongol Period (2004), п. 312.
- ^ а б Nasr, S. H., & Aminrazavi, M. (2007). Anthology of philosophy in Persia: from Zoroaster to Omar Khayyam.[ISBN missing ]
- ^ Boscaglia, F. (2015). Pessoa, Borges and Khayyam. Variaciones Borges
- ^ а б c d е ж Ross, E. (1898). Al-Musaffariyé: Containing a Recent Contribution to the Study of 'Omar Khayyām. Journal of the Royal Asiatic Society of Great Britain and Ireland, 349–366.
- ^ Aminrazavi, Mehdi. "Umar Khayyam". Стэнфордская энциклопедия философии. Получено 22 ноября 2017.
- ^ а б c d J. C. E. Bowen. (1973). The Rubāՙiyyāt of Omar Khayyam: A Critical Assessment of Robert Graves' and Omar Ali Shah's Translation. Iran, 11, 63–73.
- ^ Davis, Dick. "FitzGerald, Edward". Encyclopædia Iranica. Получено 15 января 2017.
- ^ FitzGerald, E. (2010). Rubaiyat of Omar Khayyam (p. 12). Champaign, Ill.: Project Gutenberg
- ^ Schenker, D. (1981). Fugitive Articulation: An Introduction to "The Rubáiyát of Omar Khayyam". Victorian Poetry, 19(1), 49–64.
- ^ Hedayat's "Blind Owl" as a Western Novel. Princeton Legacy Library: Michael Beard
- ^ Katouzian, H. (1991). Sadeq Hedayat: The life and literature of an Iranian writer (p. 138). London: I.B. Tauris
- ^ Bashiri, Iraj. "Hedayat's Learning".
- ^ Hitchens, C. (2007). The portable atheist: Essential readings for the nonbeliever (p. 7). Philadelphia, PA: Da Capo.
- ^ Csillik, B. (1960). ”The Real 'Omar Khayyām’”. Acta Orientalia Academiae Scientiarum Hungaricae, 10(1), 59–77. Retrieved from https://www.jstor.org/stable/23682646
- ^ Albano, G. (2008). The Benefits of Reading the "Rubáiyát of Omar Khayyám" as Pastoral. Victorian Poetry, 46(1), 55–67.
- ^ C. H. A. Bjerregaard, Sufism: Omar Khayyam and E. Fitzgerald, The Sufi Publishing Society (1915), p. 3
- ^ Idries Shah, The Sufis, Octagon Press (1999), pp. 165–166
- ^ "Every line of the Rubaiyat has more meaning than almost anything you could read in Sufi literature" Abdullah Dougan Who is the Potter? Gnostic Press 1991 ISBN 0-473-01064-X
- ^ S. H. Nasr, 2006, Islamic Philosophy from Its Origin to the Present, Chapter 9., pp. 165–183
- ^ Meyerhof, M. (1948). 'Alī al-Bayhaqī's Tatimmat Siwān al-Hikma: A Biographical Work on Learned Men of the Islam. Osiris, 8, 122–217.
- ^ e.g. by the author of Firdaws al-tawārikh (Ross 1898:356), author of Tārikh alfī (Ross 1898:358), and al-Isfahani (Aminrazavi 2007:49).
- ^ Beveridge, H. (1905). XVIII. Omar Khayyam. Journal of the Royal Asiatic Society, 37(3), 521–526.
- ^ J. D. Yohannan, Persian Poetry in England and America, 1977. p. 202.
- ^ The Great Umar Khayyam: A Global Reception of the Rubaiyat (AUP – Leiden University Press) by A. A. Seyed-Gohrab, 2012.
- ^ Simidchieva, M. (2011). FitzGerald's Rubáiyát and Agnosticism. In A. Poole, C. Van Ruymbeke, & W. Martin (Eds.), FitzGerald's Rubáiyát of Omar Khayyám: Popularity and Neglect (pp. 55–72). Anthem Press.
- ^ UNIS. "Monument to Be Inaugurated at the Vienna International Centre, 'Scholars Pavilion' donated to International Organizations in Vienna by Iran".
- ^ "Khayyam statue finally set up at University of Oklahoma". Tehran Times. Архивировано из оригинал on 5 April 2016. Получено 4 апреля 2016.
- ^ Jeffrey D. Lavoie, The Private Life of General Omar N. Bradley (2015), p. 13.
- ^ Dictionary of Minor Planet Names. 1979. стр. 255. Получено 8 September 2012 - через Google Книги.
- ^ "How Omar Khayyam changed the way people measure time". Независимый. 17 May 2019. Получено 18 мая 2019.
Рекомендации
- Browne, E. (1899). Yet More Light on 'Umar-i-Khayyām. Journal of the Royal Asiatic Society of Great Britain and Ireland, 409–420.
- Turner, Howard R. (1997). Science in Medieval Islam: An Illustrated Introduction. Техасский университет Press. ISBN 0-292-78149-0.
- Jos Biegstraaten (2008). "Omar Khayyam (Impact On Literature And Society In The West)". Энциклопедия Iranica. vol. 15. Encyclopaedia Iranica Foundation.
- Nasr, S.H. (2006). Islamic Philosophy from Its Origin to the Present: Philosophy in the Land of Prophecy. SUNY Press. ISBN 0-7914-6799-6.
- Katz, Victor (1998). A History of Mathematics: An Introduction (2-е изд.). Addison-Wesley. п.879. ISBN 0-321-01618-1.
- Knoebel, Art; Laubenbacher, Reinhard; Lodder, Jerry (2007). Mathematical Masterpieces: Further Chronicles by the Explorers. Springer. ISBN 978-0387330617.
- изд. by J.A. Boyle. (1968). The Cambridge History of Iran (5): The Saljug and Mongol Periods. Издательство Кембриджского университета. ISBN 0-521-06936-X.CS1 maint: дополнительный текст: список авторов (связь)
- Smith, David Eugene (1935). "Euclid, Omar Khayyâm, and Saccheri". Scripta Mathematica. III (1): 5–10. OCLC 14156259.
- Rozenfeld, Boris A. (1988). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space. Springer Verlag. pp. 65, 471. ISBN 0-387-96458-4.
- Ross, E. (1927). 'Omar Khayyam. Bulletin of the School of Oriental Studies, University of London, 4(3), 433–439.
- Jan Rypka (1968). History of Iranian Literature. Reidel Publishing Company. OCLC 460598. ISBN 90-277-0143-1
внешняя ссылка
- Hashemipour, Behnaz (2007). "Khayyām: Ghiyāth al‐Dīn Abū al‐Fatḥ ʿUmar ibn Ibrāhīm al‐Khayyāmī al‐Nīshāpūrī". In Thomas Hockey; и другие. (ред.). Биографическая энциклопедия астрономов. New York: Springer. pp. 627–8. ISBN 978-0-387-31022-0. (PDF version )
- Umar Khayyam, на Стэнфордская энциклопедия философии
- Khayyam's works in original Persian at Ganjoor Persian Library
- Khayyam in Tarikhema.ir
- Works by Omar Khayyam в Project Gutenberg
- Works by Omar Khayyám в Faded Page (Canada)
- Works by or about Omar Khayyam в Интернет-архив
- Works by Omar Khayyam в LibriVox (аудиокниги в общественном достоянии)

- The illustrated Rubáiyát of Omar Khayyám в Интернет-архив.
- Omar Khayyam's Rubaiyat as translated by Edward Fitzgerald – 1st edition
- The Rubaiyat by Omar Khayyam – The Internet Classics Archive
- Illustrations to the Rubaiyat by Adelaide Hanscom
- Barney Rickenbacker, Exploring Khayyaam website. Different versions of well-known quatrains compared, with notes.



