Каталонский номер - Catalan number

Названия номеров на каталонском языке см. Список номеров на разных языках § Окситано-романский.

В C₅ = 42 непересекающиеся перегородки набора из 5 элементов (ниже, остальные 10 из 52 перегородки )

В комбинаторная математика, то Каталонские числа сформировать последовательность из натуральные числа которые происходят в различных проблемы с подсчетом, часто с участием рекурсивно определенные объекты. Они названы в честь бельгийского математика. Эжен Шарль Каталан (1814–1894).

В пй каталонский номер дается непосредственно в виде биномиальные коэффициенты к

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}=\prod \limits _{k=2}^{n}{\frac {n+k}{k}}\qquad {\text{for }}n\geq 0.}$

Первые каталонские номера для п = 0, 1, 2, 3, ... являются

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 9148256133640, 34305 4861946401452, ... (последовательность A000108 в OEIS ).

Характеристики

Альтернативное выражение для C_п является

${\displaystyle C_{n}={2n \choose n}-{2n \choose n+1}={1 \over n+1}{2n \choose n}\quad {\text{ for }}n\geq 0,}$

что эквивалентно приведенному выше выражению, потому что ${\displaystyle {\tbinom {2n}{n+1}}={\tfrac {n}{n+1}}{\tbinom {2n}{n}}}$. Это показывает, что C_п является целое число, что не сразу очевидно из первой приведенной формулы. Это выражение лежит в основе доказательство правильности формулы.

Каталонские числа удовлетворяют повторяющиеся отношения^[1]

${\displaystyle C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\text{for }}n\geq 0,}$

${\displaystyle \sum _{i_{1}+\cdots +i_{m}=n,i_{1},\ldots ,i_{m}\geq 0}C_{i_{1}}\cdots C_{i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2)(n+m/2+3)\cdots (n+m)}}C_{n+m/2},&m{\text{ even}}\\[5pt]{\dfrac {m(n+1)(n+2)\cdots (n+(m-1)/2)}{(n+(m+3)/2)(n+(m+3)/2+1)\cdots (n+m)}}C_{n+(m-1)/2},&m{\text{ odd,}}\end{cases}}}$

и

${\displaystyle C_{0}=1\quad {\text{and}}\quad C_{n+1}={\frac {2(2n+1)}{n+2}}C_{n}.}$

Асимптотически числа Каталонии растут как

${\displaystyle C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}}$

в том смысле, что частное пое каталонское число и выражение справа стремится к 1 как п приближается к бесконечности. Это можно доказать, используя Приближение Стирлинга зап! или через производящие функции.

Единственные каталонские числа C_п странными являются те, для которых п = 2^k - 1; все остальные равны. Единственные простые каталонские числа: C₂ = 2 и C₃ = 5.^[2]

Каталонские числа имеют интегральное представление

${\displaystyle C_{n}=\int _{0}^{4}x^{n}\rho (x)\,dx,}$

куда ${\displaystyle \rho (x)={\tfrac {1}{2\pi }}{\sqrt {\tfrac {4-x}{x}}}.}$ Это означает, что каталонские числа являются решением одной из версий Проблема моментов Хаусдорфа.^[3]

Приложения в комбинаторике

Есть много проблем со счетом в комбинаторика решение которой дается числами Каталонии. Книга Перечислительная комбинаторика: Том 2 комбинатор Ричард П. Стэнли содержит набор упражнений, описывающих 66 различных интерпретаций каталонских чисел. Ниже приведены некоторые примеры с иллюстрациями кейсов. C₃ = 5 и C₄ = 14.

Решетка из 14 слов Дика длины 8 - ( и ) интерпретируется как вверх и вниз

• C_п это количество Слова Дайка^[4] длины 2п. Слово Дика - это нить состоящий из п Х и п Y такое, что ни один начальный сегмент строки не имеет больше Y, чем X. Например, следующие слова Дайка длины 6:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.

• Переосмысление символа X как открытого скобка и Y в скобках, C_п подсчитывает количество выражений, содержащих п пары скобок, которые совпадают правильно:

((()))     ()(())     ()()()     (())()     (()())

• C_п это количество разных способов п +1 факторы могут быть полностью в скобках (или количество способов ассоциация п заявления бинарный оператор ). За п = 3, например, у нас есть следующие пять различных скобок для четырех факторов:

((ab) c) d (a (bc)) d (ab) (cd) a ((bc) d) a (b (cd))

В ассоциэдр порядка 4 с C₄= 14 полных двоичных деревьев с 5 листьями

• Последовательные применения бинарного оператора могут быть представлены в виде полного двоичное дерево. (Бинарное дерево с корнем полный если у каждой вершины либо двое детей, либо их нет.) Отсюда следует, что C_п это число полного двоичного деревья с п + 1 лист:

• C_п это количество неизоморфных упорядоченные (или платановые) деревья с п + 1 вершины.^[5]
• C_п количество монотонных решетчатые дорожки по краям сетки с п × п квадратные клетки, не выходящие за диагональ. Монотонный путь - это путь, который начинается в нижнем левом углу, заканчивается в верхнем правом углу и полностью состоит из ребер, направленных вправо или вверх. Подсчет таких путей эквивалентен подсчету слов Дика: X означает «двигаться вправо», а Y означает «двигаться вверх».

На следующих диаграммах показан случай п = 4:

Это можно кратко представить, перечислив каталонские элементы по высоте столбца:^[6]

[0,0,0,0] [0,0,0,1] [0,0,0,2] [0,0,1,1]

[0,1,1,1] [0,0,1,2] [0,0,0,3] [0,1,1,2] [0,0,2,2] [0,0,1,3]

[0,0,2,3] [0,1,1,3] [0,1,2,2] [0,1,2,3]

Треугольники соответствуют внутренним узлам двоичных деревьев.

• А выпуклый многоугольник с п + 2 стороны можно разрезать треугольники соединяя вершины непересекающимися отрезки линии (форма триангуляция многоугольника ). Количество образованных треугольников равно п и количество различных способов, которыми это может быть достигнуто, составляет C_п. Следующие шестиугольники иллюстрируют случай п = 4:

• C_п это количество стек -сортируемый перестановки из {1, ..., п}. Перестановка ш называется сортированный по стеку если S(ш) = (1, ..., п), куда S(ш) определяется рекурсивно следующим образом: пишем ш = unv куда п это самый большой элемент в ш и ты и v являются более короткими последовательностями, и установите S(ш) = S(ты)S(v)п, с S является идентичностью для одноэлементных последовательностей.
• C_п - количество перестановок {1, ...,п} которые избегают шаблон перестановки 123 (или, как вариант, любой другой узор длиной 3); то есть количество перестановок без трехчленной возрастающей подпоследовательности. За п = 3, это перестановки 132, 213, 231, 312 и 321. Для п = 4, это 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 и 4321.
• C_п это количество непересекающиеся перегородки множества {1, ...,п}. А тем более, C_п никогда не превышает пth Номер звонка. C_п также количество непересекающихся разбиений множества {1, ..., 2п}, в котором каждый блок имеет размер 2. Соединение этих двух фактов может использоваться в доказательстве математическая индукция что все свободный кумулянты степени более 2 из Закон полукруга Вигнера равны нулю. Этот закон важен в свободная вероятность теория и теория случайные матрицы.
• C_п это количество способов укладки ступени высотой п с п прямоугольники. На следующем рисунке показан случай п = 4:

• C_п количество способов сформировать "горный хребет" с п ходы вверх и п штрихи вниз, которые остаются над горизонтальной линией. Интерпретация горного хребта состоит в том, что горы никогда не уйдут за горизонт.

• C_п это количество стандартные картины Юнга чья диаграмма представляет собой 2-хп прямоугольник. Другими словами, это количество способов, которыми числа 1, 2, ..., 2п могут быть расположены в 2-хп прямоугольник так, чтобы каждая строка и каждый столбец увеличивались. Таким образом, формула может быть получена как частный случай формула длины крючка.
• C_п - количество способов, которыми вершины выпуклого 2п-gon можно объединить в пары так, чтобы отрезки линии, соединяющие парные вершины, не пересекались. Это в точности условие, которое гарантирует, что парные ребра могут быть идентифицированы (сшиты вместе), чтобы образовать замкнутую поверхность нулевого рода (топологическую 2-сферу).
• C_п это количество полупорядки на п немаркированные предметы.^[7]
• В химическом машиностроении C_п−1 число возможных последовательностей разделения, которые могут разделить смесь п составные части.^[8]

Доказательство формулы

Есть несколько способов объяснить, почему формула

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}}$

решает комбинаторные задачи, перечисленные выше. Первое доказательство ниже использует производящая функция. Остальные доказательства являются примерами биективные доказательства; они включают в себя буквально подсчет набора каких-то объектов, чтобы прийти к правильной формуле.

Первое доказательство

Прежде всего заметим, что все комбинаторные задачи, перечисленные выше, удовлетворяют Сегнера^[9] отношение повторения

${\displaystyle C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\text{for }}n\geq 0.}$

Например, каждое слово Дайка ш длины ≥ 2 однозначно записывается в виде

ш = Xш₁Yш₂

с (возможно, пустыми) словами Дика ш₁ и ш₂.

В производящая функция для каталонских чисел определяется как

${\displaystyle c(x)=\sum _{n=0}^{\infty }C_{n}x^{n}.}$

Приведенное выше рекуррентное соотношение можно затем резюмировать в форме производящей функции соотношением

${\displaystyle c(x)=1+xc(x)^{2};}$

другими словами, это уравнение следует из рекуррентного соотношения путем разложения обеих частей в степенные ряды. С одной стороны, рекуррентное соотношение однозначно определяет каталонские числа; с другой стороны, отношение производящей функции может быть решено алгебраически, чтобы дать

${\displaystyle c(x)={\frac {1\mp {\sqrt {1-4x}}}{2x}}={\frac {2}{1\pm {\sqrt {1-4x}}}}.}$

Если выбрать знак минус (в первом выражении), дробь будет иметь степенной ряд в 0, поэтому ее коэффициенты должны быть каталонскими числами. Это решение удовлетворяет

${\displaystyle \lim _{x\to 0^{+}}c(x)=C_{0}=1}$

Другое решение со знаком плюс имеет полюс 0, поэтому оно не может быть допустимым решением для c(Икс).

Член квадратного корня можно разложить в степенной ряд, используя тождество

${\displaystyle {\sqrt {1+y}}=\sum _{n=0}^{\infty }{{\frac {1}{2}} \choose n}y^{n}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}}{4^{n}(2n-1)}}{2n \choose n}y^{n}=1+{\frac {1}{2}}y-{\frac {1}{8}}y^{2}+\cdots .}$

Это частный случай Обобщенная биномиальная теорема Ньютона; как и в случае с общей теоремой, это может быть доказано вычислением производных для получения ряда Тейлора. Параметр у = −4Икс и подставив этот степенной ряд в выражение для c(Икс) и сдвиг индекса суммирования п на 1 разложение упрощается до

${\displaystyle c(x)=\sum _{n=0}^{\infty }{2n \choose n}{\frac {x^{n}}{n+1}}.}$

Коэффициенты теперь являются желаемой формулой для C_п.

Другой способ получить c(Икс) заключается в решении для xc(Икс) и заметим, что ${\displaystyle \int _{0}^{x}\!t^{n}\,dt}$ появляется в каждом члене степенного ряда.

Второе доказательство

Рис. 1. Неверный участок пути (сплошной красный цвет) перевернут. Плохие пути достигают (п – 1, п + 1) вместо (п,п).

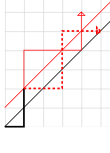
Это доказательство зависит от уловки, известной как Метод отражения Андре, который изначально использовался в связи с Теорема Бертрана о бюллетене. (Принцип отражения широко приписывается Дезире Андре, но его метод фактически не использовал отражения; а метод отражения - это вариант, созданный Эбли и Мириманов.^[10]) Считаем пути, которые начинаются и заканчиваются на диагонали п × п сетка. Все такие пути имеют п вправо и п ступеньки вверх. Поскольку мы можем выбрать, какой из 2п ступеньки восходящие (или, что то же, вправо), есть ${\displaystyle {\tbinom {2n}{n}}}$ полные монотонные траектории этого типа. А Плохо путь пересечет основную диагональ и коснется следующей более высокой (фатальный) диагональ (обозначена красным на иллюстрации). Мы переворачиваем часть пути, возникшую после этого касания, по этой фатальной диагонали, как показано на рисунке; эта геометрическая операция сводится к тому, что после этого касания меняются местами все шаги вправо и вверх. На участке пути, который не отражается, на один шаг вверх больше, чем на шаги вправо, поэтому оставшийся участок неправильного пути имеет на один шаг вправо больше, чем шаг вверх (потому что он заканчивается на главной диагонали). Когда эта часть пути отражается, она также будет иметь на один шаг вверх больше, чем шаги вправо. Поскольку есть еще 2п шаги, теперь должно быть п +1 ступенька вверх и п - 1 шаг вправо. Итак, вместо достижения цели (п,п), все плохие пути (после отражения части пути) будут заканчиваться в месте (п − 1, п + 1). Как и любой монотонный путь в (п − 1) × (п + 1) сетка должна соответствовать фатальной диагонали, этот процесс отражения устанавливает взаимное соответствие между плохими путями исходной сетки и монотонными путями этой новой сетки, потому что процесс отражения обратим. Таким образом, количество плохих путей составляет

${\displaystyle {n-1+n+1 \choose n-1}={2n \choose n-1}={2n \choose n+1}}$

и количество каталонских путей (то есть хороших путей) получается путем удаления количества плохих путей из общего количества монотонных путей исходной сетки,

${\displaystyle C_{n}={2n \choose n}-{2n \choose n+1}.}$

В терминах слов Дайка мы начинаем с (не-Дейковской) последовательности п Х и п Y и меняют местами все X и Y после первого Y, которое нарушает условие Дейка. На этом первом Y есть k +1 Y и k Х для некоторых k от 1 до п − 1.

Третье доказательство

Следующее биективное доказательство, будучи более сложным, чем предыдущее, дает более естественное объяснение термина п +1 в знаменателе формулы дляC_п. Обобщенную версию этого доказательства можно найти в статье Rukavicka Josef (2011).^[11]

Рисунок 2. Путь с превышением 5.

Предположим, нам дан монотонный путь, который может пересекать диагональ. В превосходство пути определяется как количество вертикальный края, которые лежат над диагональ. Например, на рисунке 2 ребра, лежащие выше диагонали, отмечены красным, поэтому превышение пути равно 5.

Теперь, если нам дан монотонный путь, превышение которого не равно нулю, то мы можем применить следующий алгоритм для построения нового пути, превышение которого на единицу меньше того, с которого мы начали.

• Начиная с нижнего левого угла, следуйте по пути, пока он не пройдет выше диагонали.
• Продолжайте идти по пути, пока он касается снова диагональ. Обозначим через Икс первый такой край, который достигнут.
• Поменять местами часть пути, встречавшуюся до Икс с частью, происходящей после Икс.

Следующий пример должен прояснить это. На рисунке 3 черная точка указывает точку, где путь сначала пересекает диагональ. Черный край Икс, и мы меняем местами красную часть на зеленую, чтобы создать новый путь, показанный на второй диаграмме.

Рисунок 3. Зеленая и красная части меняются местами.

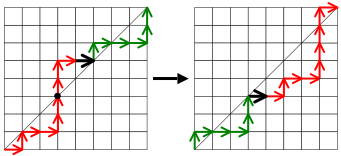
Превышение снизилось с трех до двух. Фактически, алгоритм приведет к уменьшению превышения на единицу для любого пути, который мы ему подаем, потому что первый вертикальный шаг, начинающийся по диагонали (в точке, отмеченной черной точкой), является уникальным вертикальным краем, который под действием операции переходит от диагонали сверху вниз; все остальные вертикальные края остаются на той же стороне диагонали.

Рис. 4. Все монотонные траектории в сетке 3 × 3, иллюстрирующие алгоритм уменьшения превышения.

Также нетрудно увидеть, что этот процесс обратимый: по любому пути п превышение которого меньше чем п, существует ровно один путь, который дает п когда к нему применяется алгоритм. Действительно, (черный) край Икс, которая изначально была первой горизонтальной ступенькой, оканчивающейся на диагонали, стала последний горизонтальный шаг начало по диагонали.

Это означает, что количество путей превышения п равно количеству путей превышения п - 1, что равно количеству путей превышения п - 2 и так далее до нуля. Другими словами, мы разделили набор все монотонные пути в п + 1 классы одинакового размера, соответствующие возможному превышению от 0 до п. Поскольку есть

${\displaystyle {2n \choose n}}$

монотонных путей, получаем искомую формулу

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}.}$

Рисунок 4 иллюстрирует ситуацию дляп = 3. Каждый из 20 возможных монотонных путей появляется где-то в таблице. В первом столбце показаны все пути превышения трех, которые полностью лежат выше диагонали. Столбцы справа показывают результат последовательных применений алгоритма с уменьшением превышения на единицу за раз. Всего пять рядов, то естьC₃ = 5.

Четвертое доказательство

В этом доказательстве используется определение каталонских чисел триангуляцией, чтобы установить связь между C_п и C_п+1. Учитывая многоугольник п с п + 2 стороны, сначала отметьте одну из его сторон как основу. Если п триангулируется, мы можем выбрать и сориентировать один из двухп + 1 ребро. Есть (4п + 2)C_п такие украшенные триангуляции. Теперь дан многоугольник Q с п + 3 стороны, снова обозначьте одну из его сторон как основу. Если Q триангулирован, мы можем дополнительно отметить одну из сторон, отличную от основной. Есть (п + 2)C_п + 1 такие украшенные триангуляции. Тогда существует простое соответствие между этими двумя видами украшенных триангуляций: мы можем либо свернуть треугольник в Q чья сторона отмечена, или наоборот расширить ориентированный край в п треугольнику и отметьте его новую сторону. Таким образом

${\displaystyle (4n+2)C_{n}=(n+2)C_{n+1}.}$

Биномиальная формула для C_п непосредственно следует из этого соотношения и начального условияC₁ = 1.

Пятое доказательство

Это доказательство основано на Слова Дайка интерпретация каталонских чисел, поэтому C_п количество способов правильно сопоставить п пары скоб. Обозначим a (возможно, пустой) правильный строка с c и его обратное (где "[" и "]" меняются местами) с c⁺. Поскольку любой c можно однозначно разложить на c = [ c₁ ] c₂, суммируя возможные точки для размещения закрывающей скобки, немедленно дает рекурсивное определение

${\displaystyle C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\text{for }}n\geq 0.}$

Теперь позвольте б стоять за сбалансированный строка длины 2п- то есть содержащие равное количество «[» и «]» - и ${\displaystyle \textstyle B_{n}={2n \choose n}=d_{n}C_{n}}$ с некоторым фактором d_п ≥ 1. Как и выше, любую сбалансированную строку можно однозначно разложить на [c ] б или же ]c⁺ [ б, так

${\displaystyle B_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}.}$

Кроме того, любая неверно сбалансированная строка начинается с c ], так

${\displaystyle B_{n+1}-C_{n+1}=\sum _{i=0}^{n}{2i+1 \choose i}C_{n-i}=\sum _{i=0}^{n}{\frac {2i+1}{i+1}}B_{i}C_{n-i}.}$

Вычитая приведенные выше уравнения и используя B_я = d_я C_я дает

${\displaystyle C_{n+1}=2\sum _{i=0}^{n}d_{i}C_{i}C_{n-i}-\sum _{i=0}^{n}{\frac {2i+1}{i+1}}d_{i}C_{i}C_{n-i}=\sum _{i=0}^{n}{\frac {d_{i}}{i+1}}C_{i}C_{n-i}.}$

Сравнение коэффициентов с исходной формулой рекурсии для C_п дает d_я = я +1, так что

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}.}$

Шестое доказательство

Это простое доказательство^[12] также основан на Слова Дайка интерпретация каталонских чисел, но использует красивую лемму Цикла Дворецкого и Моцкина.^[13]Назовите последовательность X и Y доминирующий если, читая слева направо, дисбаланс всегда положительно, то есть количество X всегда строго больше, чем количество Y. Лемма о цикле утверждает, что любая последовательность ${\displaystyle m}$ Х и ${\displaystyle n}$ Y's, где ${\displaystyle m>n}$, имеет точно ${\displaystyle m-n}$ доминирующие циклические перестановки. Чтобы в этом убедиться, просто расставьте заданную последовательность ${\displaystyle m+n}$ X и Y по кругу и несколько раз удаляйте соседние пары XY, пока только ${\displaystyle m-n}$ Х остаются. Каждый из этих X был началом доминирующей циклической перестановки до того, как что-либо было удалено. ${\displaystyle m=n+1}$, существует ровно одна доминирующая циклическая перестановка. Удаление ведущего X из него (доминирующая последовательность должна начинаться с X) оставляет последовательность Дика. Поскольку есть ${\displaystyle C_{n}={\frac {1}{2n+1}}{2n+1 \choose n}={\frac {1}{n+1}}{2n \choose n}}$ отдельные циклы ${\displaystyle n+1}$ Х и ${\displaystyle n}$ Y, каждая из которых соответствует ровно одной последовательности Дика, ${\displaystyle C_{n}}$ считает последовательности Дика.

Матрица Ганкеля

В п×п Матрица Ганкеля чей (я, j) entry - каталонское число C_я+j−2 имеет детерминант 1, независимо от значения п. Например, для п = 4 имеем

${\displaystyle \det {\begin{bmatrix}1&1&2&5\\1&2&5&14\\2&5&14&42\\5&14&42&132\end{bmatrix}}=1.}$

Более того, если индексацию «сдвинуть» так, что (я, j) запись заполнена каталонским числом C_я+j−1 то определитель по-прежнему равен 1, независимо от значения п. Например, для п = 4 имеем

${\displaystyle \det {\begin{bmatrix}1&2&5&14\\2&5&14&42\\5&14&42&132\\14&42&132&429\end{bmatrix}}=1.}$

Взятые вместе, эти два условия однозначно определяют каталонские числа.

История

Каталонские числа в книге Минганту Быстрый метод получения точного отношения деления окружности том III

Каталонская последовательность была описана в 18 веке Леонард Эйлер, которого интересовало количество различных способов разделить многоугольник на треугольники. Последовательность названа в честь Эжен Шарль Каталан, который обнаружил связь с выражениями в скобках во время исследования Башни Ханоя головоломка. Трюк со счетом слов Дика был найден Дезире Андре в 1887 г.

В 1988 году выяснилось, что каталонская числовая последовательность использовалась в Китай монгольским математиком Минганту к 1730 г.^[14][15] Именно тогда он начал писать свою книгу Гэ Юань Ми Лу Цзе Фа [Быстрый метод получения точного отношения деления круга], который был завершен его учеником Чэнь Цзисинь в 1774 году, но опубликован шестьдесят лет спустя. Питер Дж. Ларкомб (1999) обрисовал некоторые особенности работы Минганту, в том числе стимул Пьера Жарту, который принес в Китай три бесконечные серии в начале 1700-х годов.

Например, Мин использовал каталонскую последовательность, чтобы выразить разложение в ряды sin (2α) и sin (4α) через sin (α).

Обобщения

Двухпараметрическая последовательность неотрицательных целых чисел ${\displaystyle {\frac {(2m)!(2n)!}{(m+n)!m!n!}}}$является обобщением каталонских чисел. Они названы супер-каталонские числа, к Ира Гессель. Это число не следует путать с Числа Шредера – Гиппарха, которые иногда также называют суперкаталонскими числами.

За ${\displaystyle m=1}$, это всего лишь в два раза больше обычных каталонских чисел, а для ${\displaystyle m=n}$, числа имеют простое комбинаторное описание, однако другие комбинаторные описания известны только^[16]за ${\displaystyle m=2,3}$ и ${\displaystyle 4}$,^[17]и это открытая проблема - найти общую комбинаторную интерпретацию.

Сергей Фомин и Натан Ридинг дали обобщенное каталонское число, связанное с любой конечной кристаллографической Группа Коксетера, а именно количество полностью коммутативных элементов группы; с точки зрения связанных корневая система, это количество антицепей (или идеалов порядка) в наборе положительных корней. Классический каталонский номер ${\displaystyle C_{n}}$ соответствует корневой системе типа ${\displaystyle A_{n}}$. Классическое рекуррентное соотношение является обобщающим: каталонское число диаграммы Кокстера равно сумме каталонских чисел всех ее максимальных собственных поддиаграмм.^[18]

Смотрите также

• Математический портал

• Ассоциэдр
• Теорема Бертрана о бюллетене
• Биномиальное преобразование
• Каталонский треугольник
• Каталонское число Мерсенна
• Суетиться – каталонское число
• Список факториальных и биномиальных тем
• Номера лобби
• Число Нараяны
• Число Шредера – Гиппарха
• Решетка Тамари
• Число Веддерберна – Этерингтона

Примечания

1. Bowman, D .; Регев, Алон (2014). «Считающая симметрия: классы разрезов выпуклого правильного многоугольника». Adv. Appl. Математика. 56: 35–55. Дои:10.1016 / j.aam.2014.01.004. S2CID  15430707.
2. Коши, Томас; Салмасси, Мохаммад (2006). «Четность и простота каталонских чисел» (PDF). Математический журнал колледжа. 37 (1): 52–53. Дои:10.2307/27646275. JSTOR  27646275.
3. Чой, Хайён; Йе, Ён-Нан; Ю, Сонук (2020), «Каталонские числовые последовательности и последовательности моментов Хаусдорфа», Дискретная математика, 343 (5): 111808, 11, arXiv:1809.07523, Дои:10.1016 / j.disc.2019.111808, МИСТЕР  4052255
4. Эквивалентные определения путей Дика
5. Стэнли, стр.221, пример (e)
6. Чрепиншек, Матей; Мерник, Лука (2009). «Эффективное представление для решения проблем, связанных с каталонскими числами» (PDF). Международный журнал чистой и прикладной математики. 56 (4): 589–604.
7. Kim, K. H .; Roush, F. W. (1978), "Перечисление классов изоморфизма полупорядков", Журнал комбинаторики, информации и системных наук, 3 (2): 58–61, МИСТЕР  0538212.
8. Томпсон, Р. У .; Кинг, К. Дж. (1972), "Систематический синтез схем разделения", Журнал Айше, 18 (5): 941–948, Дои:10.1002 / aic.690180510.
9. А. де Сегнер, Enumeratio modorum, quibus figurae planae rectilineae per diagonales dividuntur in triangula. Новые комментарии academiae scientiarum Petropolitanae 7 (1758/59) 203–209.
10. Рено, Марк (2008). «Утрачено (и найдено) в переводе: реальный метод Андре и его применение к общей проблеме голосования» (PDF). Американский математический ежемесячный журнал. 115 (4): 358–363. Дои:10.1080/00029890.2008.11920537. S2CID  8126326.
11. Рукавицкая Йозеф (2011), Об обобщенных путях Дайка, Электронный журнал комбинаторики онлайн
12. Дершовиц, Начум; Закс, Шмуэль (1980), "Перечень упорядоченных деревьев", Дискретная математика, 31: 9–28, Дои:10.1016 / 0012-365x (80) 90168-5, HDL:2027 / uiuo.ark: / 13960 / t3kw6z60d
13. Дворецкий, Арье; Моцкин, Теодор (1947), "Проблема аранжировок", Математический журнал герцога, 14 (2): 305–313, Дои:10.1215 / s0012-7094-47-01423-3
14. Ларкомб, Питер Дж. «Китайское открытие каталонских чисел в 18 веке» (PDF).
15. «Мин Анту, первый в мире изобретатель каталонских чисел».
16. Чен, Синь; Ван, Джейн (2012). «Супер-каталонские числа S (m, m + s) для s ≤ 4». arXiv:1208.4196 [math.CO ].
17. Георгичук Ирина; Ореловиц, Гидон (2020). «Супер-каталонские числа третьего и четвертого рода». arXiv:2008.00133 [math.CO ].
18. Сергей Фомин и Натан Ридинг, «Корневые системы и обобщенные ассоциаэдры», Геометрическая комбинаторика, IAS / Park City Math. Сер. 13, Американское математическое общество, Провиденс, Род-Айленд, 2007 г., стр. 63–131. arXiv:математика / 0505518

Рекомендации

• Стэнли, Ричард П. (2015), Каталонские числа. Издательство Кембриджского университета, ISBN  978-1-107-42774-7.
• Конвей и Парень (1996) Книга чисел. Нью-Йорк: Коперник, стр. 96–106.
• Гарднер, Мартин (1988), Путешествие во времени и другие математические недоумения, Нью-Йорк: W.H. Фримен и компания, стр.253–266 (гл. 20), ISBN  0-7167-1924-X
• Коши, Томас (2008), Каталонские номера с приложениями, Издательство Оксфордского университета, ISBN  978-0-19-533454-8
• Коши, Томас и Чжэнгуанг Гао (2011) "Некоторые свойства делимости каталонских чисел", Математический вестник 95:96–102.
• Ларкомб, П.Дж. (1999). «Китайское открытие каталонских чисел в 18 веке» (PDF). Математический спектр. 32: 5–7.
• Стэнли, Ричард П. (1999), Перечислительная комбинаторика. Vol. 2, Кембриджские исследования по высшей математике, 62, Издательство Кембриджского университета, ISBN  978-0-521-56069-6, МИСТЕР  1676282
• Эгечиоглу, Омер (2009), Каталонская оценка детерминанта Ханкеля (PDF)
• Георгичук Ирина; Ореловиц, Гидон (2020), Суперкаталонские числа третьего и четвертого рода, arXiv:2008.00133

внешняя ссылка

• Стэнли, Ричард П. (1998), Каталонское приложение к Enumerative Combinatorics, Volume 2 (PDF)
• Вайсштейн, Эрик В. «Каталонский номер». MathWorld.
• Дикау, Роберт М .: Каталонские числа Дальнейшие примеры.
• Дэвис, Том: Каталонские числа. Еще примеры.
• «Эквивалентность трех интерпретаций каталонских чисел» от проекта Wolfram Demonstrations [1]
• Учебные материалы, связанные с Числовые треугольники, связанные с разделами в Викиверситете