Решетчатый путь - Lattice path

В комбинаторика, а решетчатый путь в длины с шагами в это последовательность так что каждая последовательная разница лежит в .[1] Решетчатый путь может лежать в любом решетка в ,[1] но целочисленная решетка чаще всего используется.
Пример решетчатого пути в длиной 5 с шагом в является .
Решетчатые дорожки Северо-Восток
А Северо-восточный (NE) решетчатый путь решетчатый путь в с шагами в . В шаги называются северными шагами и обозначаются s; ступени называются восточными ступенями и обозначаются с.
Пути решетки NE обычно начинаются в начале координат. Это соглашение позволяет нам кодировать всю информацию о пути решетки NE. в единственном слово перестановки. Длина слова дает нам количество шагов на пути решетки, . Порядок проведения 'песок передает последовательность . Кроме того, количество и количество в слове определяет конечную точку .
Если слово перестановки для цепочки NE содержит шаги и шагов, и если путь начинается в начале координат, то путь обязательно заканчивается в . Это следует потому, что вы точно "прошли" шаги на север и шагов к востоку от .

Подсчет решетчатых путей
Решетчатые пути часто используются для подсчета других комбинаторных объектов. Точно так же существует множество комбинаторных объектов, которые подсчитывают количество путей решетки определенного типа. Это происходит, когда пути решетки находятся в биекция с рассматриваемым объектом. Например,
- Дайковые тропы подсчитываются Каталонский номер . А Дайк путь решетчатый путь в из к с шагами в что никогда не проходит ниже -ось.[2] Эквивалентно, путь Дика - это путь решетки NE от к который лежит строго ниже (но может касаться) диагонали .[2][3]
- В Числа Шредера подсчитать количество путей решетки из к с шагами в и которые никогда не поднимаются выше диагонали .[2]
- Количество путей решетки NE от к считает количество комбинации из объекты из набора объекты.
Комбинации и решетки NE
Дорожки решетки NE имеют тесные связи с количеством комбинации, которые считаются биномиальный коэффициент, и расположены в Треугольник Паскаля. На приведенной ниже схеме показаны некоторые из этих подключений.
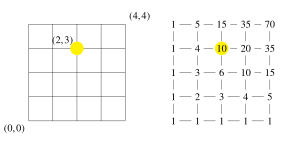
Число путей решетки от к равно биномиальный коэффициент . Схема показывает это для . Если повернуть диаграмму на 135 ° по часовой стрелке вокруг начала координат и расширить ее, чтобы включить все , получаем треугольник Паскаля. Этот результат неудивителен, потому что вступление Строка Треугольника Паскаля - это биномиальный коэффициент .
Проблемы и доказательства
Графическое представление путей решетки NE подходит для многих биективный доказательства, включающие комбинации. Вот несколько примеров.
- .
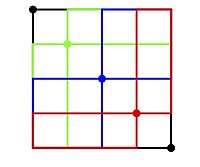
Доказательство: Правая часть равна количеству путей решетки NE из к . Каждый из этих путей решетки NE пересекает ровно одну из точек решетки в прямоугольном массиве с координатами за . Это показано на рисунке ниже для : Каждый путь решетки NE от к пересекает ровно один из цветных узлов.

С левой стороны биномиальный коэффициент в квадрате , представляет собой две копии набора путей решетки NE из к присоединенная конечная точка к начальной точке. Поверните вторую копию на 90 ° по часовой стрелке. Это не меняет комбинаторику объекта: . Таким образом, общее количество путей решетки остается прежним.

Наложите квадраты путей решетки NE на тот же прямоугольный массив, как показано на рисунке ниже. Мы видим, что все пути решетки NE из к учитываются. В частности, обратите внимание, что любой путь решетки, проходящий через красную точку решетки (например), считается возведенным в квадрат набором путей решетки (также показанным красным).
Рекомендации
- ^ а б Стэнли, Ричард (2012). Перечислительная комбинаторика, Том 1 (2-е изд.). Издательство Кембриджского университета. п. 21. ISBN 978-1-107-60262-5.
- ^ а б c Стэнли, Ричард (2001). Перечислительная комбинаторика, Том 2. Издательство Кембриджского университета. С. 173, 239. ISBN 978-0-521-78987-5.
- ^ "Wolfram MathWorld". Получено 6 марта 2014.


















































