Модели распределения ниши - Niche apportionment models

Механистические модели распределения ниши - это биологические модели, используемые для объяснения относительное обилие видов раздачи. Эти нишевые модели распределения Опишите, как виды распадаются ресурс бассейн в многомерном пространстве, определяющий распределение численности особей между видами. Относительная численность видов обычно выражается в виде графика Уиттекера или графика рангового обилия, где виды ранжируются по количеству особей на оси абсцисс, а на оси ординат откладывается логарифм относительной численности каждого вида. Относительная численность может быть измерена как относительное количество особей внутри вида или относительная биомасса особей внутри вида.

История

Модели распределения ниши были разработаны, потому что экологи искали биологические объяснения относительное обилие видов раздачи. Макартур (1957, 1961),[1][2] был одним из первых, кто выразил недовольство чисто статистические модели, представляя вместо этого 3 механистические модели распределения ниш. Макартур считал, что экологические ниши внутри пула ресурсов может быть разбит на части, как палка, причем каждая часть палки представляет ниши, занятые в сообществе. При участии Сугихары (1980),[3] Токеши (1990, 1993, 1996)[4][5][6] расширил модель сломанной палки, когда он создал примерно 7 механистических моделей распределения ниш. Эти механистические модели служат полезной отправной точкой для описания видового состава сообществ.

Описание

Рис. 1. График Уиттакера. Оцените численность для 7 наиболее часто рассматриваемых механистических моделей для распределения ниш. Модели с более крутыми склонами, такие как модель преимущественного доминирования, представляют менее ровные сообщества, где несколько видов очень многочисленны, а численность остальных видов резко снижается (см. Ровность видов ). В качестве альтернативы модели с мелким наклоном, такие как модель доминирования распада, представляют более ровные сообщества, в которых многие виды одинаково многочисленны, а относительно небольшое количество видов - редкость.

Модель распределения ниш может использоваться в ситуациях, когда один пул ресурсов последовательно или одновременно разбивается на более мелкие ниши путем колонизации видов или видообразования (пояснение по использованию ресурсов: виды внутри гильдии используют одни и те же ресурсы, а виды внутри сообщества не могут ).

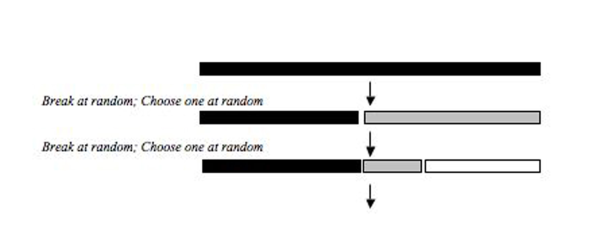
Эти модели описывают, как виды, которые черпают из одного и того же пула ресурсов (например, гильдия (экология) ) разделить свою нишу. Пул ресурсов разбивается либо последовательно, либо одновременно, и два компонента процесса фрагментации ниши включают выбор фрагмента и размер полученного фрагмента (рис. 2).

Модели распределения ниши использовались в первичной литературе для объяснения и описания изменений в распределении относительной численности разнообразных таксонов, включая пресноводных насекомых, рыб, мохообразных жуков, паразитов перепончатокрылых, сообщества планктона и солончаковых трав.

Предположения

Рисунок 2. Механизмы взлома ниши. Ресурсный пул разделен на ниши разного размера, что может быть выражено в относительной численности видов в общем пуле ресурсов.

Механистические модели, которые описывают эти графики, работают в предположении, что ранжированные графики численности основаны на строгой оценке численности особей внутри видов и что эти меры представляют фактическое распределение численности видов. Более того, независимо от того, используется ли количество особей в качестве меры численности или биомасса особей, эти модели предполагают, что это количество прямо пропорционально размеру ниши, занимаемой организмом. Одно из предположений состоит в том, что численность, измеряемая как количество особей, может иметь меньшие отклонения, чем у тех, кто биомасса. Таким образом, некоторые исследования, использующие изобилие как показатель распределения ниш, могут переоценить ровность из сообщество. Это происходит потому, что нет четкого различия между размером тела, изобилие (экология), и ресурс использовать. Часто исследованиям не удается включить размерную структуру или оценки биомассы в показатели фактической численности, и эти показатели могут создавать более высокую дисперсию моделей распределения ниш, чем численность, измеряемая строго как количество особей.[7][8]

Механистические модели распределения ниши Токеши

Ниже описаны семь механистических моделей, описывающих распределение ниши. Модели представлены в порядке возрастания ровности, от наименее ровной модели Dominance Pre-emption до наиболее даже моделей Dominance Decay и MacArthur Fraction.

Превышение доминирования

Эта модель описывает ситуацию, когда после первоначальной колонизации (или видообразования) каждый новый вид занимает более 50% наименьшей оставшейся ниши. В модели распределения ниш с вытеснением доминирования виды колонизируют случайную часть от 50 до 100% наименьшей оставшейся ниши, что делает эту модель стохастической по своей природе. Тесно родственная модель, геометрическая серия,[9] является детерминированной версией модели упреждения доминирования, в которой процент оставшегося нишевого пространства, который занимает новый вид (k), всегда одинаков. Фактически, модели упреждения доминирования и геометрические ряды концептуально схожи и будут давать такое же распределение относительной численности, когда доля заполненной ниши меньшего размера всегда равна 0,75. Модель упреждающего доминирования лучше всего подходит для распределения относительной численности некоторых сообществ речных рыб в Техас, включая некоторые таксономические группы и конкретные функциональные группы.[10]

Геометрический (k = 0,75)

Доминирование-preemption.svg

Случайный ассортимент

В модели случайного ассортимента пул ресурсов случайным образом делится между одновременно или последовательно колонизирующими видами. Эта закономерность может возникнуть из-за того, что мера численности не масштабируется в зависимости от количества ниши, занимаемой видом, или потому, что временные изменения численности видов или ширины ниши вызывают нарушение последовательности в распределении ниш с течением времени, и, таким образом, виды, похоже, не имеют взаимосвязи между степенью занятости и их ниша. Токеши (1993)[5] объяснил, что эта модель во многом схожа с нейтральной теорией биоразнообразия Касвелла, главным образом потому, что виды действуют независимо друг от друга.

Случайная дробь

Модель случайных фракций описывает процесс, в котором размер ниши выбирается случайным образом путем последовательной колонизации видов. Первоначальный вид выбирает случайную часть общей ниши, а последующие колонизирующие виды также выбирают случайную часть общей ниши и случайным образом делят ее, пока все виды не колонизируются. Токеши (1990)[4] обнаружили, что эта модель совместима с некоторыми сообществами эпифитных креветок-хиромонид, и в последнее время она использовалась для объяснения распределения относительной численности сообществ фитопланктона, солончаковой растительности, некоторых сообществ насекомых отряда Diptera, некоторых сообществ жужелиц, функциональных и функциональных. таксономические группы речных рыб в биорегионах Техаса и ихневмонидные паразитоиды. Подобная модель была разработана Сугихарой ​​в попытке дать биологическое объяснение логарифмически нормального распределения Престона (1948).[11] Сугихара (1980)[3] Модель фиксированного деления была похожа на модель случайной дроби, но случайность модели получена из треугольное распределение со средним значением 0,75, а не нормальным распределением со средним значением 0,5, используемым в случайной фракции. Сугихара использовал треугольное распределение, чтобы нарисовать случайные величины, потому что случайность некоторых природных популяций соответствует треугольному распределению со средним значением 0,75.

Случайная дробь.svg

Доля мощности

Эта модель может объяснить распределение относительной численности, когда вероятность колонизации существующей ниши в пуле ресурсов положительно связана с размером этой ниши (измеряется как численность, биомасса и т. Д.). Вероятность колонизации части ниши зависит от относительных размеров установленных ниш и масштабируется показателем k. k может принимать значение от 0 до 1, и если k> 0, всегда немного выше вероятность того, что большая ниша будет колонизирована. Эта модель считается более реалистичной с биологической точки зрения, потому что можно представить множество случаев, когда ниша с большей долей ресурсов с большей вероятностью будет захвачена, потому что в этой нише больше места для ресурсов и, следовательно, больше возможностей для приобретения. Модель случайной доли распределения ниши - это крайность модели доли власти, где k = 0, и другая крайность модели доли власти, когда k = 1, напоминает модель фракции Макартура, где вероятность колонизации прямо пропорциональна размеру ниши.[6][12]

Мощность-фракция.svg

Фракция Макартура

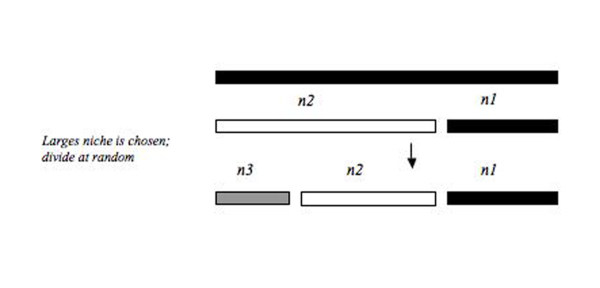
Эта модель требует, чтобы начальная ниша была разбита случайным образом, а последующие ниши выбирались с вероятностью, пропорциональной их размеру. В этой модели самая большая ниша всегда имеет большую вероятность быть сломанной по сравнению с меньшими нишами в пуле ресурсов. Эта модель может привести к более равномерному распределению, при котором более крупные ниши с большей вероятностью будут нарушены, облегчая сосуществование видов в нишах одинакового размера. В основе модели фракции Макартура лежит сломанная палка, разработанная Макартуром (1957). Эти модели дают схожие результаты, но одно из основных концептуальных различий заключается в том, что ниши заполняются одновременно в модели Broken Stick, а не последовательно, как во фракции Макартура. Токеши (1993)[5] утверждает, что последовательное вторжение в пул ресурсов более биологически реалистично, чем одновременное нарушение нишевого пространства. Когда численность рыбы из всех биорегионов Техаса была объединена, распределение напоминало модель распределения ниш со сломанной палкой, что предполагает относительно равномерное распределение видов пресноводных рыб в Техасе.[10]

Макартур-фракция.svg

Распад господства

Эту модель можно рассматривать как противоположность модели упреждения доминирования. Во-первых, первоначальный пул ресурсов заселяется случайным образом, а оставшиеся, последующие колонизаторы всегда колонизируют самую большую нишу, независимо от того, колонизирована она уже или нет. Эта модель генерирует наиболее равномерное сообщество по сравнению с описанными выше моделями распределения ниш, поскольку самая большая ниша всегда разбивается на два меньших фрагмента, которые с большей вероятностью будут эквивалентны размеру меньшей ниши, которая не была нарушена. Сообщества такого «уровня» ровности кажутся редкостью в природных системах. Однако одно из таких сообществ включает распределение относительной численности фильтраторов на одном участке в пределах реки Дунай в Австрии.[13]

Доминирование-decay.svg

Композитный

Составная модель существует, когда комбинация моделей распределения ниш действует в разных частях пула ресурсов. Фесл (2002).[13] показывает, как может выглядеть составная модель при исследовании пресноводных Двукрылые, в том смысле, что разные модели распределения ниш подходят для разных функциональных групп данных. Другой пример, проведенный Хиггинсом и Штраусом (2008), моделирующий сообщества рыб, показал, что сообщества рыб из разных местообитаний и с различным составом видов соответствуют различным моделям распределения ниш, таким образом, все сообщество видов представляет собой комбинацию моделей в различных регионах ареала видов. .

Подгонка механистических моделей распределения ниши к эмпирическим данным

Механистические модели распределения ниши предназначены для описания сообществ. Исследователи использовали эти модели разными способами, чтобы исследовать временные и географические тенденции в изобилии видов.

В течение многих лет подбор моделей распределения ниш проводился на глаз, а графики моделей сравнивались с эмпирическими данными.[5] Совсем недавно были разработаны статистические тесты соответствия моделей распределения ниш эмпирическим данным.[14][15] Более поздний метод (Etienne and Ollf 2005)[15] использует байесовское моделирование моделей для проверки их соответствия эмпирическим данным. Первый метод, который все еще широко используется, моделирует ожидаемую относительную численность на основе нормального распределения каждой модели при том же количестве видов, что и эмпирические данные. Каждая модель моделируется несколько раз, и можно рассчитать среднее значение и стандартное отклонение для определения доверительных интервалов вокруг каждого распределения относительной численности. Достоверность каждого ранга можно проверить по эмпирическим данным для каждой модели, чтобы определить соответствие модели. Доверительные интервалы рассчитываются следующим образом.[4][12] Для получения дополнительной информации о моделировании моделей распределения ниш на сайте [1][постоянная мертвая ссылка ], который объясняет программу Power Niche.[14]

r = доверительный предел смоделированных данных σ = стандартное отклонение смоделированных данных = количество повторов эмпирической выборки

использованная литература

  1. ^ Макартур, Р. Х. (1957). Об относительном обилии видов птиц. Proc. Natl. Акад. Sci. 43, 293-295.
  2. ^ Макартур, Р. Х. Макартур, Дж. У. (1961). О видовом разнообразии птиц. Экология. 42, 594-598.
  3. ^ а б Сугихара, Г. (1980). Минимальная структура сообщества: объяснение закономерностей обилия видов. Am. Nat. 116. 770-787.
  4. ^ а б c Токеши, М. (1990). Распределение ниши или случайный ассортимент: пересмотр моделей численности видов. Журнал экологии животных. 59, 1129–1146.
  5. ^ а б c d Токеши, М. (1993). Структура видового обилия и структура сообщества. Adv. Ecol. Res. 24, 112-186.
  6. ^ а б Токеши, М. (1996). Power Fraction: новое объяснение моделей обилия видов в богатых видами сообществах. Ойкос. 75, 543-550.
  7. ^ Гастон, К. В. Блэкберн, Т. М. (2000). Макроэкология, Оксфорд, Великобритания: Blackwell Science.
  8. ^ Конус, М. Л. Марке, П. А. (1996). Как виды на самом деле делят ресурсы? Американский натуралист. 147, 1072-1086.
  9. ^ Мэй, Р. М. (1975). Закономерности обилия и разнообразия видов. В экологии и эволюции сообществ. 81-120, Кембридж, Массачусетс: Издательство Гарвардского университета.
  10. ^ а б Хиггинс, К. Л. Штраус, Р. Э. (2008). Моделирование скоплений речных рыб с помощью моделей распределения ниш: закономерности. процессы и масштабная зависимость. Сделки Американского рыболовного общества. 137, 696-706.
  11. ^ Prestion, F. W. (1948). Распространенность и редкость видов. Экология. 29, 254–253.
  12. ^ а б Магуррран, А. Э. (2004). Измерение биологического разнообразия. Оксфорд, Великобритания: Blackwell Science
  13. ^ а б Фесл, К. (2002). Модели численности видов, ориентированные на нишу: различные подходы и их применение к сообществам личинок хирономид (Diptera) в большой реке. J. Anim. Ecol. 71, 1085-1094.
  14. ^ а б Дрозд, П. Новотный, В. (2000). Power Niche: модели разделения ниши для анализа сообщества. Версия 1. Руководство и программа опубликованы на сайте www.entu.cas / png / PowerNiche.
  15. ^ а б Этьен, Р. С. Оллф, Х. (2005). Сопоставление различных моделей структуры сообщества с данными о численности видов: сравнение байесовских моделей. Письма об экологии. 8, 493-504.